[SPQ] If 𝑦=log tan(𝜋/4+𝑥/2), then prove that 𝒅𝒚/𝒅𝒙−𝐬𝐞𝐜𝒙=𝟎

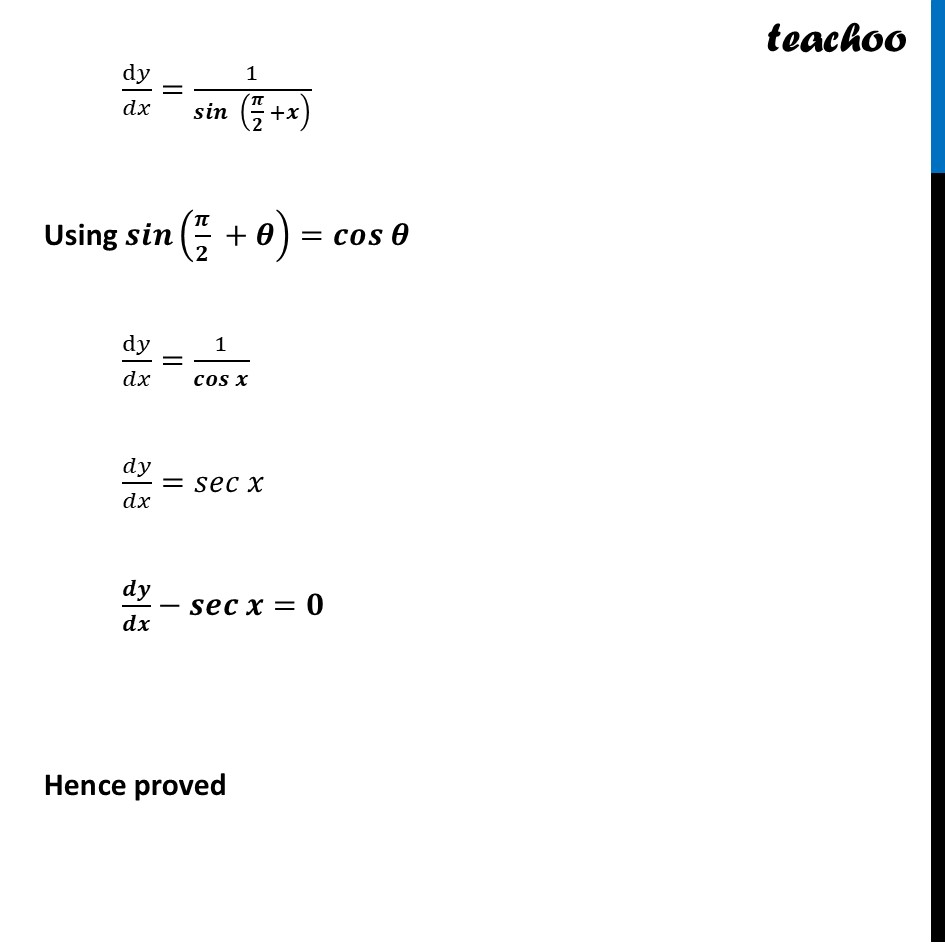
Question 22 If 𝑦=log tan(𝜋/4+𝑥/2), then prove that 𝒅𝒚/𝒅𝒙−𝐬𝐞𝐜𝒙=𝟎 Now, 𝑦=log tan(𝜋/4+𝑥/2) Differentiating both sides w.r.t x d𝑦/𝑑𝑥=(log tan(𝜋/4+𝑥/2))^′ d𝑦/𝑑𝑥=1/(tan (𝜋/4 + 𝑥/2) ) (tan (𝜋/4 + 𝑥/2))^′ d𝑦/𝑑𝑥=1/(tan (𝜋/4 + 𝑥/2) ) ×sec^2⁡(𝜋/4 + 𝑥/2) × (𝑥/2)^′ d𝑦/𝑑𝑥=𝟏/(𝐭𝐚𝐧 (𝝅/𝟒 + 𝒙/𝟐) ) ×〖𝐬𝐞𝐜〗^𝟐⁡(𝝅/𝟒 + 𝒙/𝟐) ×𝟏/𝟐 d𝑦/𝑑𝑥=cot (𝜋/4 + 𝑥/2)×sec^2⁡(𝜋/4 + 𝑥/2) ×1/2 d𝑦/𝑑𝑥=〖cos 〗⁡(𝜋/4 + 𝑥/2)/sin⁡〖 (𝜋/4 + 𝑥/2)〗 ×1/cos^2⁡(𝜋/4 + 𝑥/2) ×1/2 d𝑦/𝑑𝑥=1/(𝟐 𝒔𝒊𝒏⁡〖 (𝝅/𝟒 + 𝒙/𝟐)〗〖𝐜𝐨𝐬 〗⁡(𝝅/𝟒 + 𝒙/𝟐) ) Using 2 sin A cos A = sin 2A d𝑦/𝑑𝑥=1/𝒔𝒊𝒏⁡〖 𝟐 × (𝝅/𝟒 + 𝒙/𝟐)〗 d𝑦/𝑑𝑥=1/𝒔𝒊𝒏⁡〖 (𝝅/𝟐 +𝒙)〗 Using 𝒔𝒊𝒏(𝝅/𝟐 +𝜽)=𝒄𝒐𝒔 𝜽 d𝑦/𝑑𝑥=1/(𝒄𝒐𝒔 𝒙) 𝑑𝑦/𝑑𝑥=𝑠𝑒𝑐 𝑥 𝒅𝒚/𝒅𝒙−𝒔𝒆𝒄 𝒙=𝟎 Hence proved

Question 22 - CBSE Class 12 Sample Paper for 2026 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Davneet Singh

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular