Question 19 - CBSE Class 12 Sample Paper for 2026 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Transcript

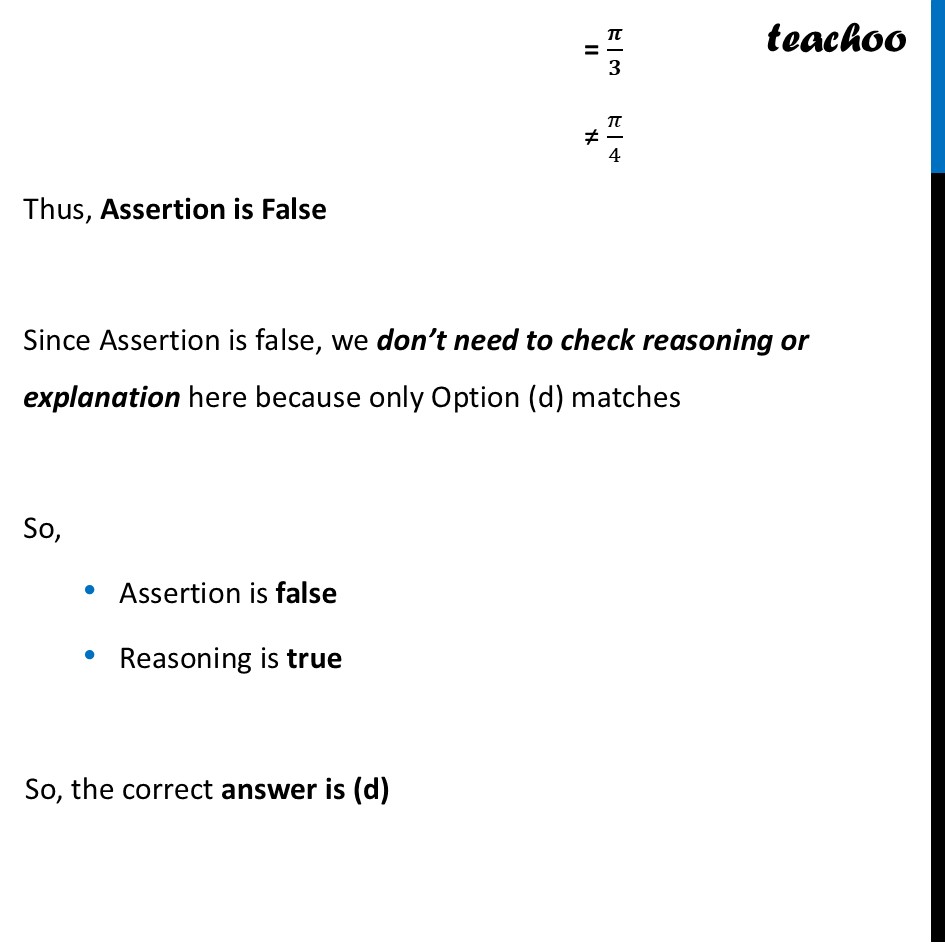
Question 19 Assertion (A): Value of the expression sin^(−1) (√3/2)+tan^(−1) 1−sec^(−1) (√2) is 𝜋/4. Reason (R): Principal value branch of sin^(−1) 𝑥 is [−𝜋/2,𝜋/2] and that of sec^(−1) 𝑥 is [0,𝜋]−{𝜋/2}. Select the correct answer from the options (A), (B), (C) and (D) as given below.) (A) Both (A) and (R) are true and (R) is the correct explanation of (A). (B) Both (A) and (R) are true but (R) is not the correct explanation of (A). (C) (A) is true but (R) is false. (D) (A) is false but (R) is true.Checking Assertion Assertion (A): Value of the expression sin^(−1) (√3/2)+tan^(−1) 1−sec^(−1) (√2) is 𝜋/4. Now, 𝐬𝐢𝐧⁡〖𝟔𝟎°〗=sin⁡〖𝜋/3〗=√3/2 𝐭𝐚𝐧⁡〖𝟒𝟓°〗=tan⁡〖𝜋/4〗=1 𝐬𝐞𝐜⁡〖𝟒𝟓°〗=sec⁡〖𝜋/4〗=√2 Thus, 〖𝒔𝒊𝒏〗^(−𝟏) (√𝟑/𝟐)+〖𝒕𝒂𝒏〗^(−𝟏) 𝟏−〖𝒔𝒆𝒄〗^(−𝟏) (√𝟐) = 𝜋/3+𝜋/4−𝜋/4 = 𝝅/𝟑 ≠ 𝜋/4 Thus, Assertion is False Since Assertion is false, we don’t need to check reasoning or explanation here because only Option (d) matches So, Assertion is false Reasoning is true So, the correct answer is (d)