Question 9 - NCERT Exemplar - MCQs - Chapter 5 Class 12 Continuity and Differentiability

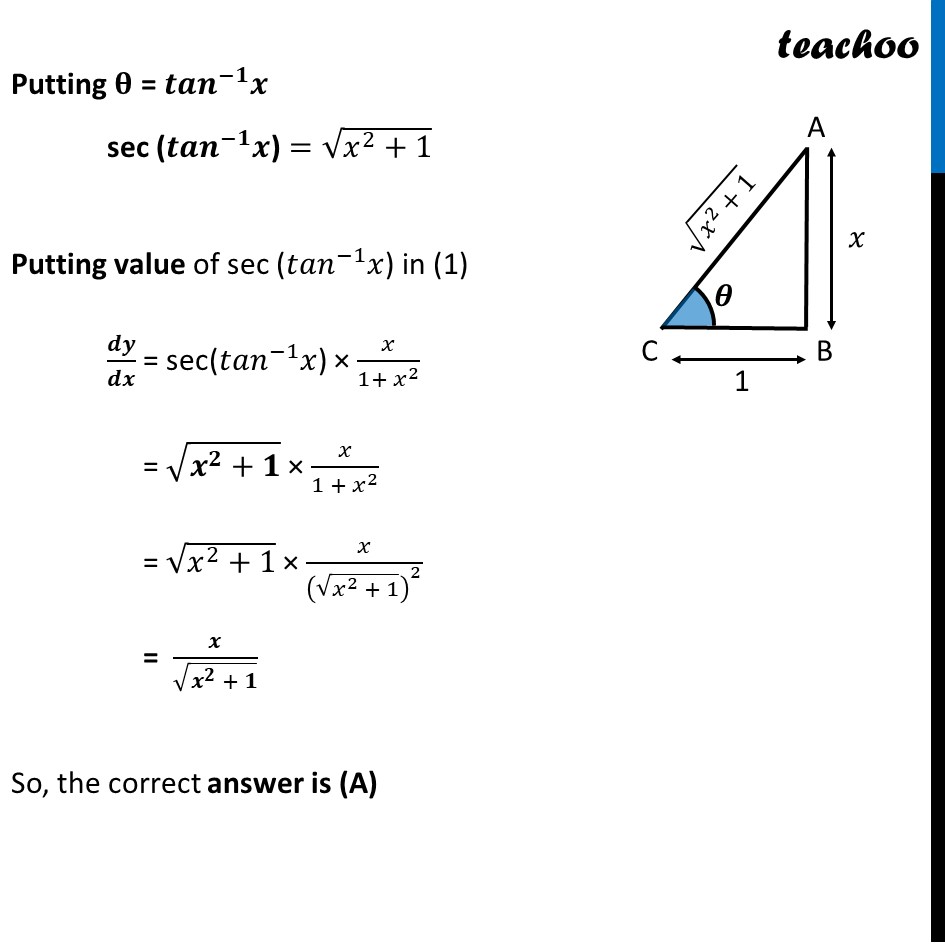
Transcript

Question 9 Differential coefficient of sec (〖𝑡𝑎𝑛〗^(−1)x) w.r.t. x is (A) 𝑥/√(1 + 𝑥^2 ) (B) 𝑥/(1 + 𝑥^2 ) (C) x √(1+𝑥^2 ) (D) 1/√(1 + 𝑥^2 ) Let y = sec (〖𝑡𝑎𝑛〗^(−1) 𝑥) Differential coefficient sec (〖𝑡𝑎𝑛〗^(−1)x) means 𝒅𝒚/𝒅𝒙 Finding 𝒅𝒚/𝒅𝒙 𝒅𝒚/𝒅𝒙 = 𝑑(sec⁡(〖𝑡𝑎𝑛〗^(−1) 𝑥))/𝑑𝑥 = sec (〖𝑡𝑎𝑛〗^(−1) 𝑥) tan (〖𝒕𝒂𝒏〗^(−𝟏) 𝒙) × (𝑑(〖𝑡𝑎𝑛〗^(−1) 𝑥))/𝑑𝑥 = sec (〖𝑡𝑎𝑛〗^(−1) 𝑥) . 𝒙 . 1/(1 + 𝑥^2 ) = sec(〖𝒕𝒂𝒏〗^(−𝟏) 𝒙) × 𝒙/(𝟏 + 𝒙^𝟐 ) Now, to find 𝒅𝒚/𝒅𝒙 , we need to find value of sec(〖𝒕𝒂𝒏〗^(−𝟏) 𝒙) Finding value of sec(〖𝒕𝒂𝒏〗^(−𝟏) 𝒙) Let 𝜽 = 〖𝒕𝒂𝒏〗^(−𝟏) 𝒙 tan⁡𝜃=𝑥 Now, let ABC be a triangle tan⁡𝜃=𝐴𝐵/𝐵𝐶 𝑥=𝐴𝐵/𝐵𝐶 𝐴𝐵/𝐵𝐶=𝑥/1 ∴ AB = 𝒙 & BC = 1 So, AC = √(〖𝐴𝐵〗^2+〖𝐵𝐶〗^2 ) = √(𝑥^2+1^2 ) = √(𝒙^𝟐+𝟏) Now, cos⁡〖𝜃=𝐵𝐶/𝐴𝐶〗 =1/√(𝑥^2 + 1) ∴ 𝐬𝐞𝐜⁡𝜽=1/cos⁡𝜃 =1/(1/√(𝑥^2+1)) =√(𝒙^𝟐+𝟏) Putting 𝛉 = 〖𝒕𝒂𝒏〗^(−𝟏) 𝒙 sec (〖𝒕𝒂𝒏〗^(−𝟏) 𝒙) =√(𝑥^2+1) Putting value of sec (〖𝑡𝑎𝑛〗^(−1) 𝑥) in (1) 𝒅𝒚/𝒅𝒙 = sec(〖𝑡𝑎𝑛〗^(−1) 𝑥) × 𝑥/(1+ 𝑥^2 ) = √(𝒙^𝟐+𝟏) × 𝑥/(1 + 𝑥^2 ) = √(𝑥^2+1) × 𝑥/(√(𝑥^2 + 1))^2 = 𝒙/√(𝒙^𝟐 + 𝟏) So, the correct answer is (A)