Question 10 - Examples - Chapter 1 Class 12 Relation and Functions

Transcript

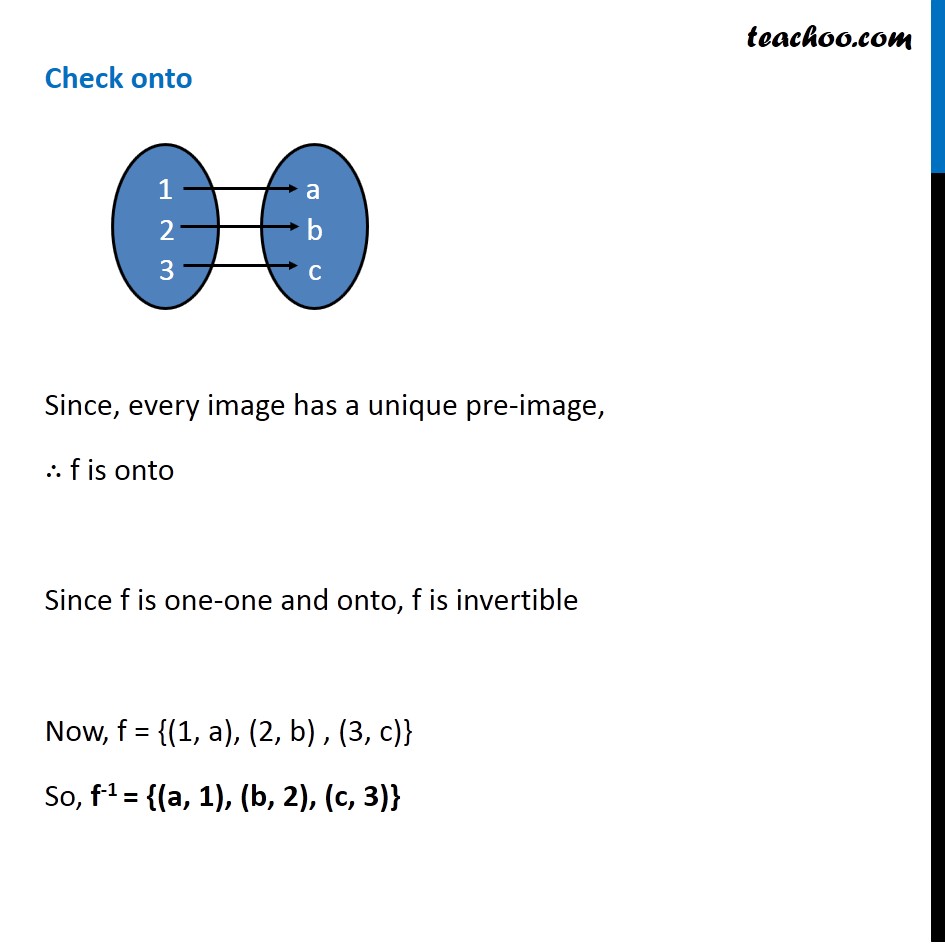
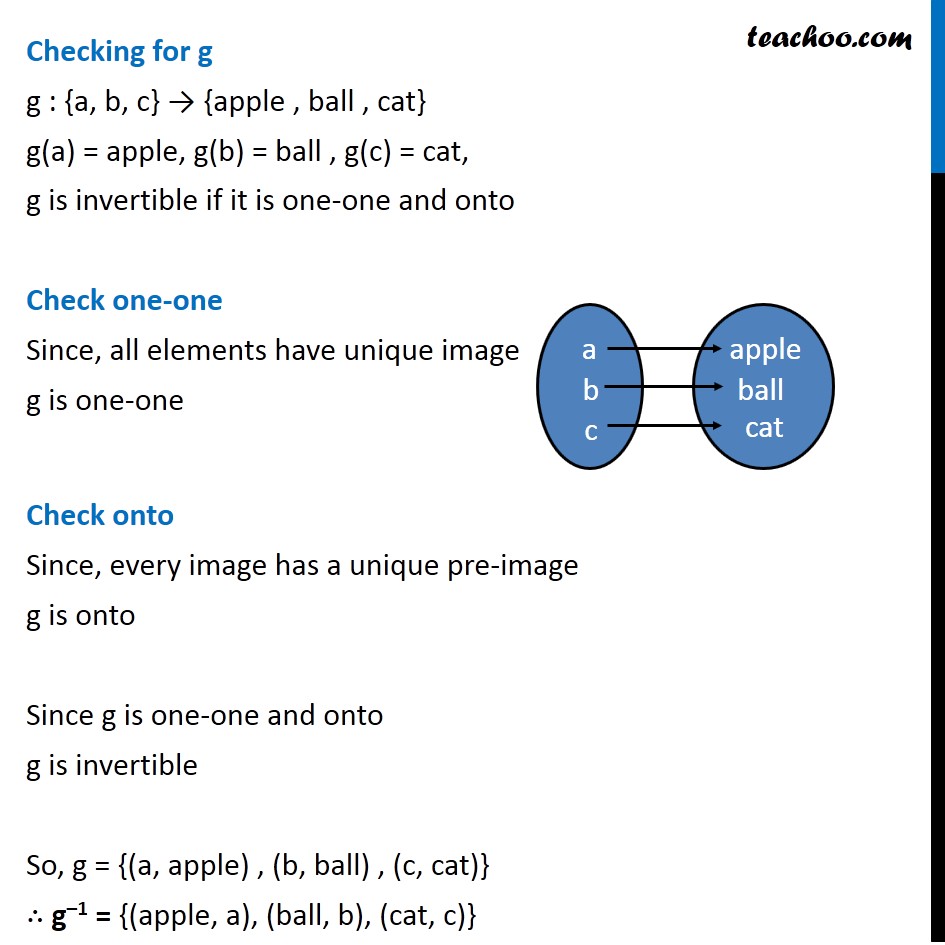
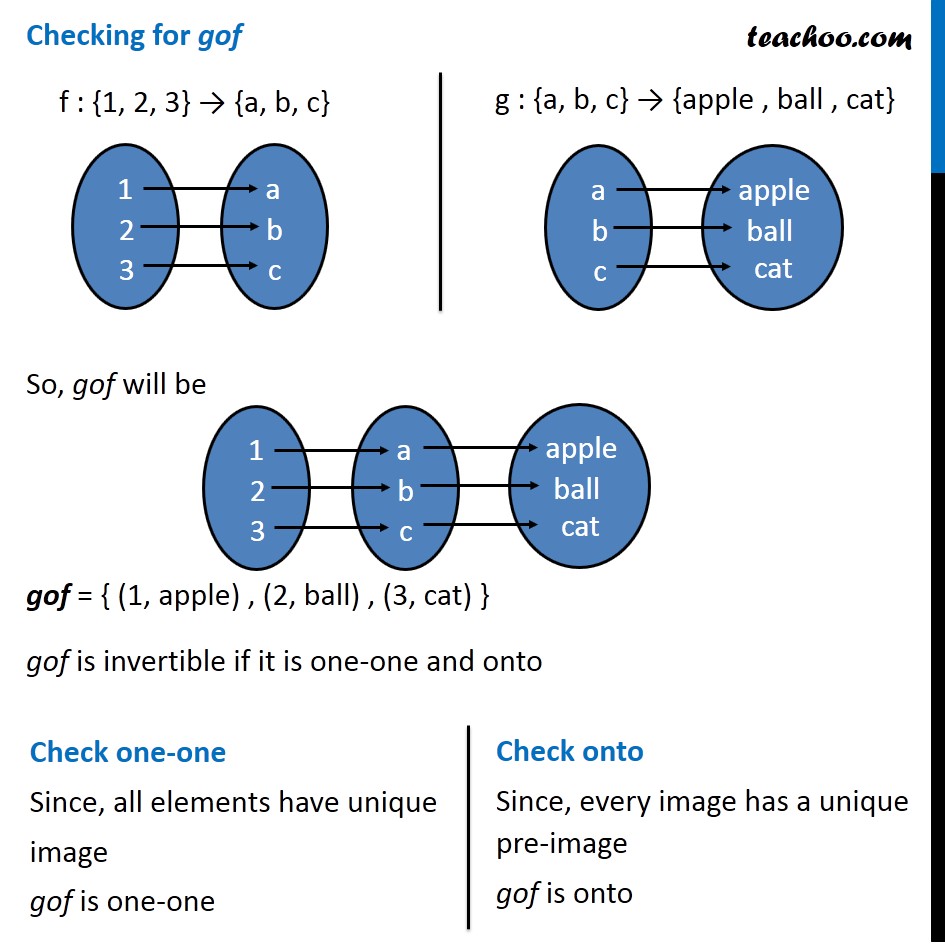
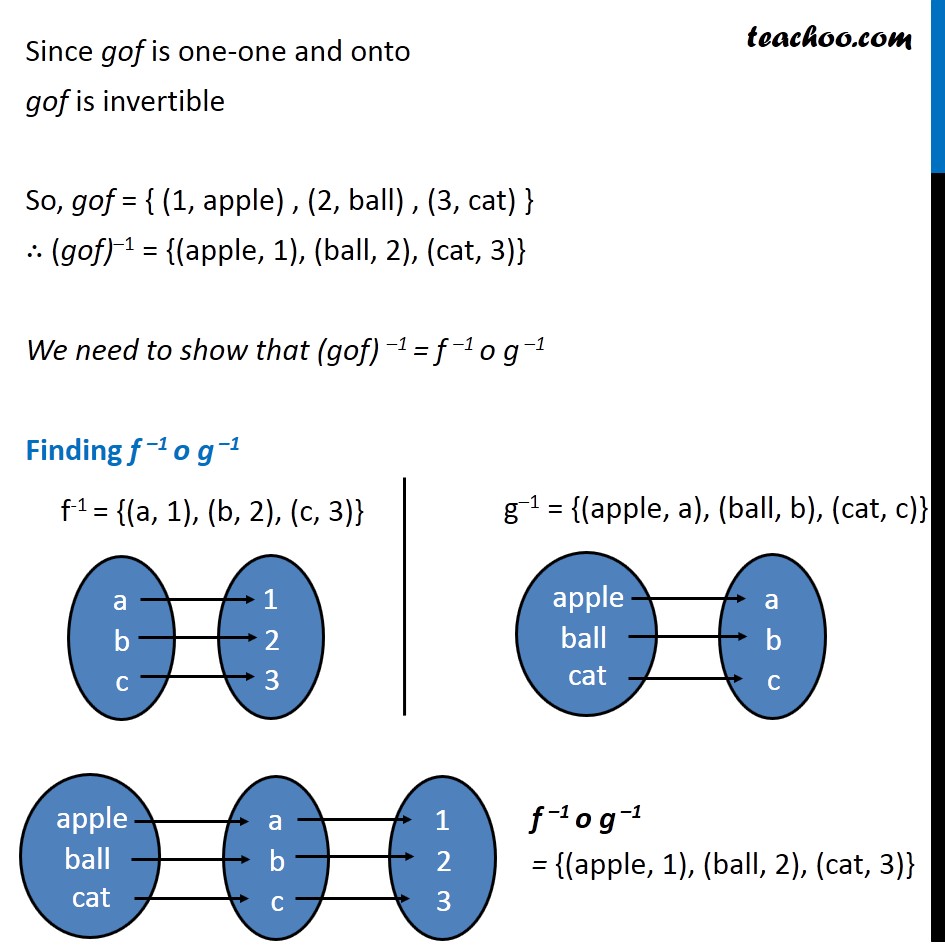
Question 10 Consider f : {1, 2, 3} → {a, b, c} and g : {a, b, c} → {apple, ball, cat} defined as f (1) = a, f (2) = b, f (3) = c, g(a) = apple, g(b) = ball and g(c) = cat. Show that f, g and gof are invertible. Find out f –1, g –1 and (gof) –1 and show that (gof) –1 = f –1 o g –1. Checking for f f : {1, 2, 3} → {a, b, c} f (1) = a, f (2) = b, f (3) = c, f is invertible if it is one-one and onto Check one-one Since, all elements have unique image f is one-one Check onto Since, every image has a unique pre-image, ∴ f is onto Since f is one-one and onto, f is invertible Now, f = {(1, a), (2, b) , (3, c)} So, f-1 = {(a, 1), (b, 2), (c, 3)} Checking for g g : {a, b, c} → {apple , ball , cat} g(a) = apple, g(b) = ball , g(c) = cat, g is invertible if it is one-one and onto Check one-one Since, all elements have unique image g is one-one Check onto Since, every image has a unique pre-image g is onto Since g is one-one and onto g is invertible So, g = {(a, apple) , (b, ball) , (c, cat)} ∴ g–1 = {(apple, a), (ball, b), (cat, c)} Checking for gof So, gof will be gof = { (1, apple) , (2, ball) , (3, cat) } gof is invertible if it is one-one and onto Check one-one Since, all elements have unique image gof is one-one Check onto Since, every image has a unique pre-image gof is onto Since gof is one-one and onto gof is invertible So, gof = { (1, apple) , (2, ball) , (3, cat) } ∴ (gof)–1 = {(apple, 1), (ball, 2), (cat, 3)} We need to show that (gof) –1 = f –1 o g –1 Finding f –1 o g –1 f-1 = {(a, 1), (b, 2), (c, 3)} g–1 = {(apple, a), (ball, b), (cat, c)} Hence, (gof)–1 = {(apple, 1), (ball, 2), (cat, 3)} f –1 o g –1= {(apple, 1), (ball, 2), (cat, 3)} Thus, (gof) –1 = f –1 o g –1 Hence proved