Check sibling questions

Ex 12.2, 11 (iv) - Chapter 12 Class 11 Limits and Derivatives

Last updated at May 29, 2023 by

Ex 13.2, 11 - Chapter 13 Class 11 Limits and Derivatives - Part 7

Ex 13.2, 11 - Chapter 13 Class 11 Limits and Derivatives - Part 8
Ex 13.2, 11 - Chapter 13 Class 11 Limits and Derivatives - Part 9

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

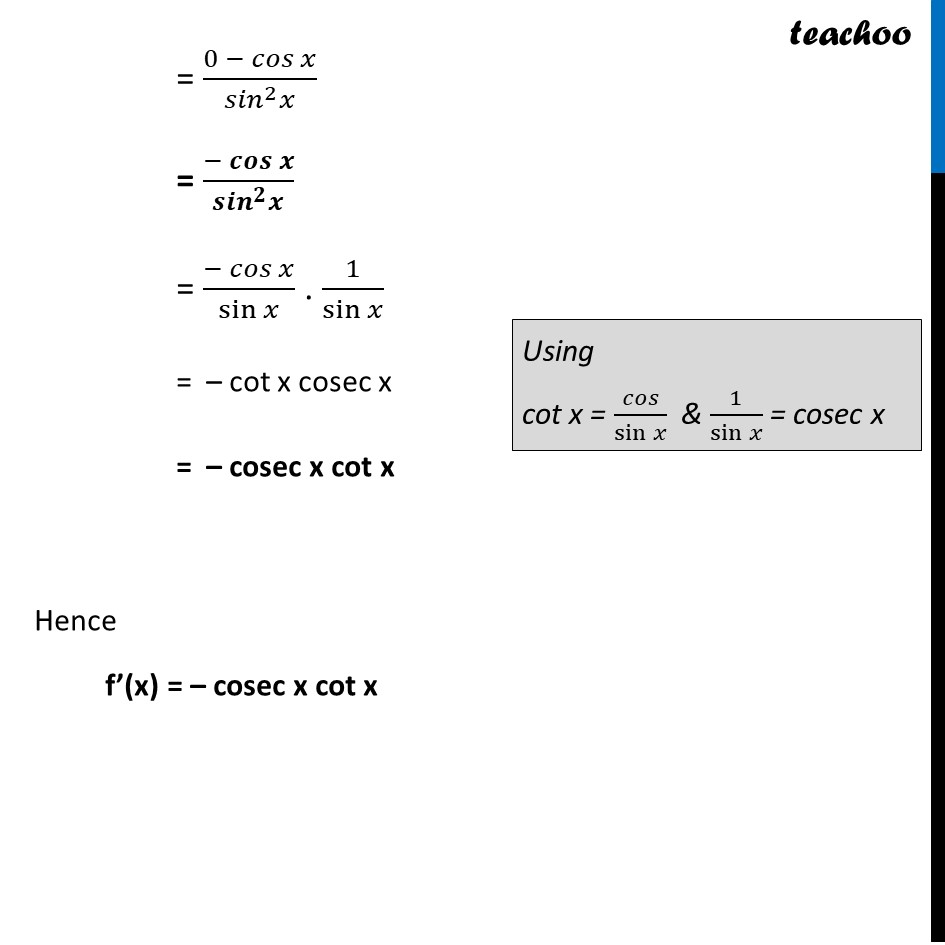
Ex 12.2, 11 Find the derivative of the following functions: (iv) cosec x Let f (x) = cosec x f(x) = 1/sin⁡𝑥 Let u = 1 & v = sin x ∴ f(x) = 𝑢/𝑣 So, f’(x) = (𝑢/𝑣)^′ Using quotient rule f’(x) = (𝑢^′ 𝑣 −〖 𝑣〗^′ 𝑢)/𝑣^2 Finding u’ & v’ u = 1 u’ = 0 & v = sin x v’ = cos x Now, f’(x) = (𝑢^′ 𝑣 −〖 𝑣〗^′ 𝑢)/𝑣^2 = (0 (sin⁡〖𝑥) −〖 cos〗⁡〖𝑥 (1)〗 〗)/(〖𝑠𝑖𝑛〗^2 𝑥) (Derivative of constant function = 0) (Derivative of sin x = cos x) = (0 − 𝑐𝑜𝑠 𝑥)/(〖𝑠𝑖𝑛〗^2 𝑥) = (− 𝑐𝑜𝑠 𝑥)/(〖𝑠𝑖𝑛〗^2 𝑥) = (− 𝑐𝑜𝑠 𝑥)/sin⁡𝑥 . 1/sin⁡𝑥 = – cot x cosec x = – cosec x cot x Hence f’(x) = – cosec x cot x Using cot x = 𝑐𝑜𝑠/sin⁡𝑥 & 1/sin⁡𝑥 = cosec x

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.