Question 27 (Or 1st) - CBSE Class 12 Sample Paper for 2019 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Transcript

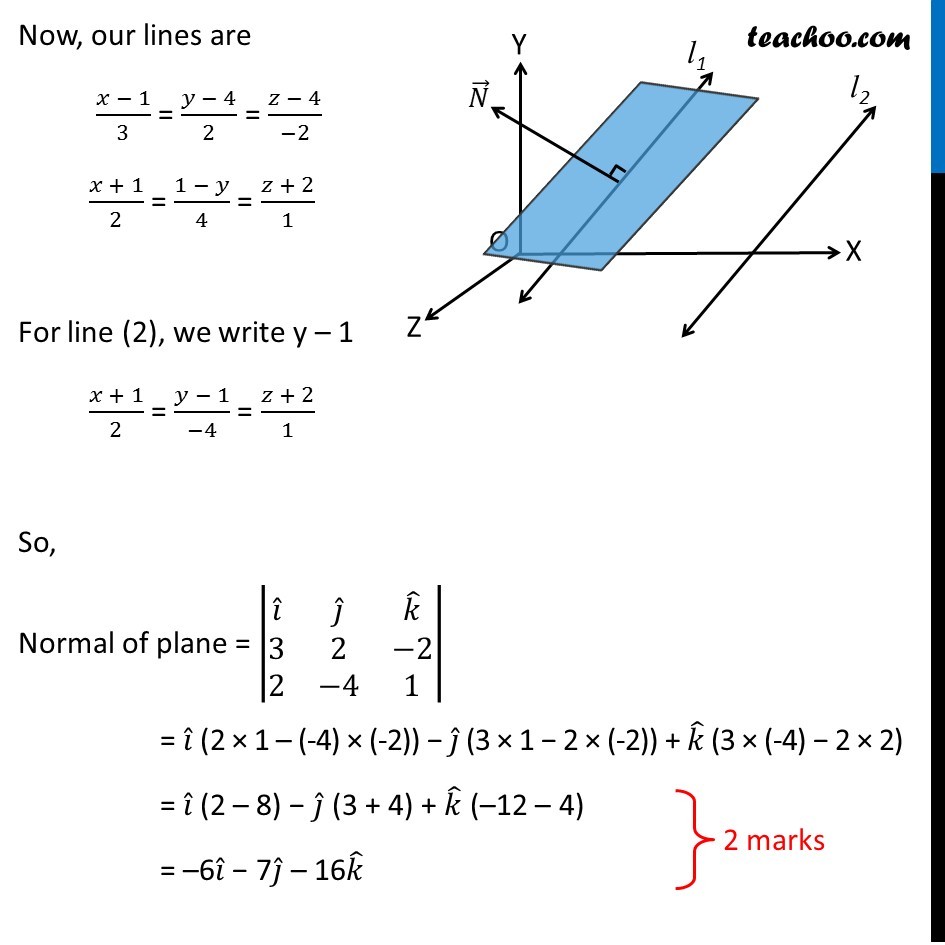
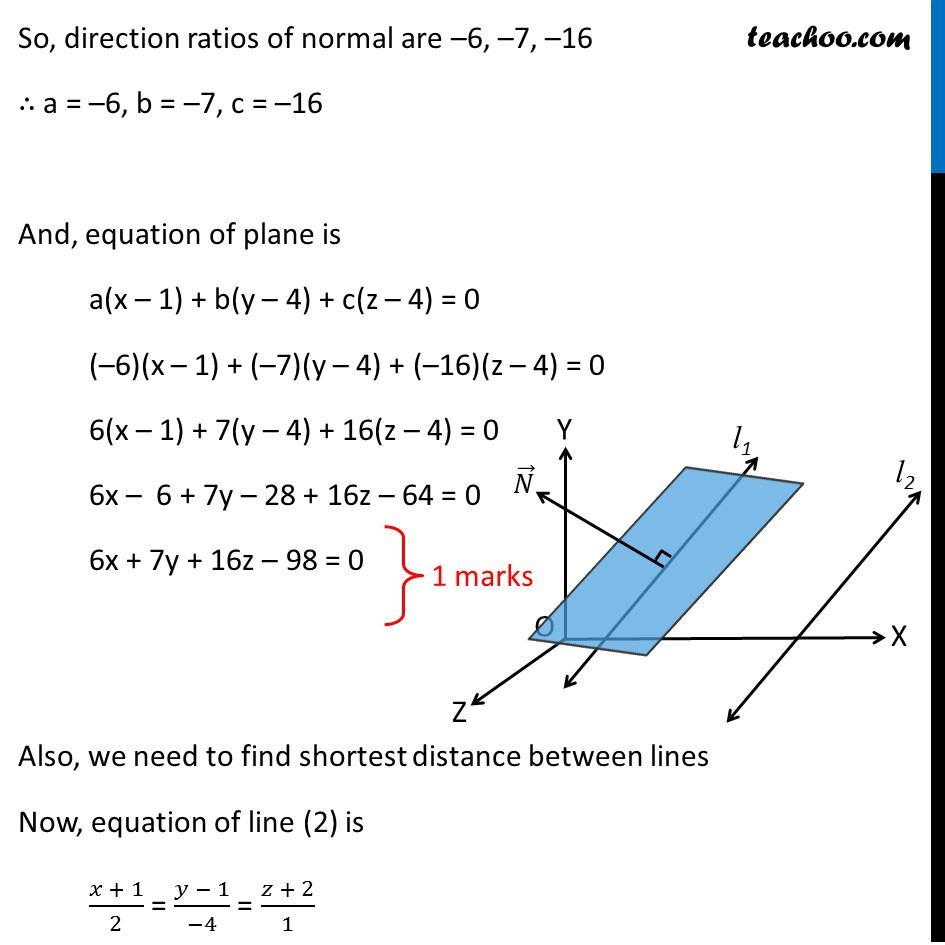
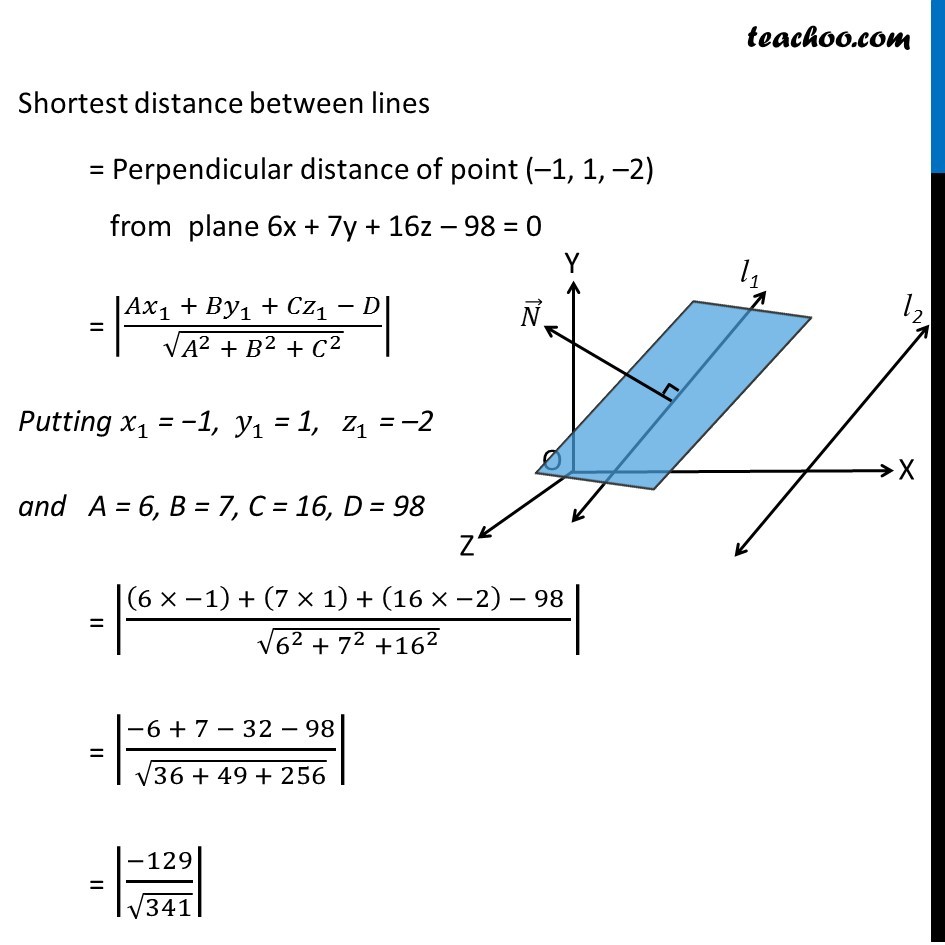
Question 27 (OR 1st question) Find the equation of the plane through the line (𝑥 − 1)/3 = (𝑦 − 4)/2 = (𝑧 − 4)/(−2) and parallel to the line (𝑥 + 1)/2 = (1 − 𝑦)/4 = (𝑧 + 2)/1 . Hence, find the shortest distance between the lines Given lines (𝑥 − 1)/3 = (𝑦 − 4)/2 = (𝑧 − 4)/(−2) (𝑥 + 1)/2 = (1 − 𝑦)/4 = (𝑧 + 2)/1 Since the plane passes through line (1) All points of line (1) will be in the plane Now, for line (1) (1, 4, 4) lies in line (1) So, plane passes through (1, 4, 4). Thus, the equation of plane is a(x – 1) + b(y – 4) + c(z – 4) = 0 Where a, b, c are the direction ratios of normal to the plane Now, given that plane is parallel to line (2) ∴ Plane is parallel to line (1) and (2) Thus, Normal of plane is perpendicular to both line (1) and (2) ∴ Normal will be cross product of parallel vectors of line (1) and (2) Now, our lines are (𝑥 − 1)/3 = (𝑦 − 4)/2 = (𝑧 − 4)/(−2) (𝑥 + 1)/2 = (1 − 𝑦)/4 = (𝑧 + 2)/1 For line (2), we write y – 1 (𝑥 + 1)/2 = (𝑦 − 1)/(−4) = (𝑧 + 2)/1 So, Normal of plane = |■8(𝑖 ̂&𝑗 ̂&𝑘 ̂@3&2&−2@2&−4&1)| = 𝑖 ̂ (2 × 1 – (-4) × (-2)) − 𝑗 ̂ (3 × 1 − 2 × (-2)) + 𝑘 ̂ (3 × (-4) − 2 × 2) = 𝑖 ̂ (2 – 8) − 𝑗 ̂ (3 + 4) + 𝑘 ̂ (–12 – 4) = –6𝑖 ̂ − 7𝑗 ̂ – 16𝑘 ̂ So, direction ratios of normal are –6, –7, –16 ∴ a = –6, b = –7, c = –16 And, equation of plane is a(x – 1) + b(y – 4) + c(z – 4) = 0 (–6)(x – 1) + (–7)(y – 4) + (–16)(z – 4) = 0 6(x – 1) + 7(y – 4) + 16(z – 4) = 0 6x – 6 + 7y – 28 + 16z – 64 = 0 6x + 7y + 16z – 98 = 0 Also, we need to find shortest distance between lines Now, equation of line (2) is (𝑥 + 1)/2 = (𝑦 − 1)/(−4) = (𝑧 + 2)/1 Shortest distance between lines = Perpendicular distance of point (–1, 1, –2) from plane 6x + 7y + 16z – 98 = 0 = |(𝐴𝑥_1 + 〖𝐵𝑦〗_1 +〖 𝐶𝑧〗_1 − 𝐷)/√(𝐴^2 + 𝐵^2 + 𝐶^2 )| Putting 𝑥_1 = −1, 𝑦_1 = 1, 𝑧_1 = –2 and A = 6, B = 7, C = 16, D = 98 = |((6 × −1) + (7 × 1) + (16 × −2) − 98 )/√(6^2 + 7^2 +16^2 )| = |(−6 + 7 − 32 − 98)/√(36 + 49 + 256)| = |(−129)/√341| = 129/√341 Thus, shortest distance 𝟏𝟐𝟗/√𝟑𝟒𝟏 units