Question 26 (OR 1 st question)
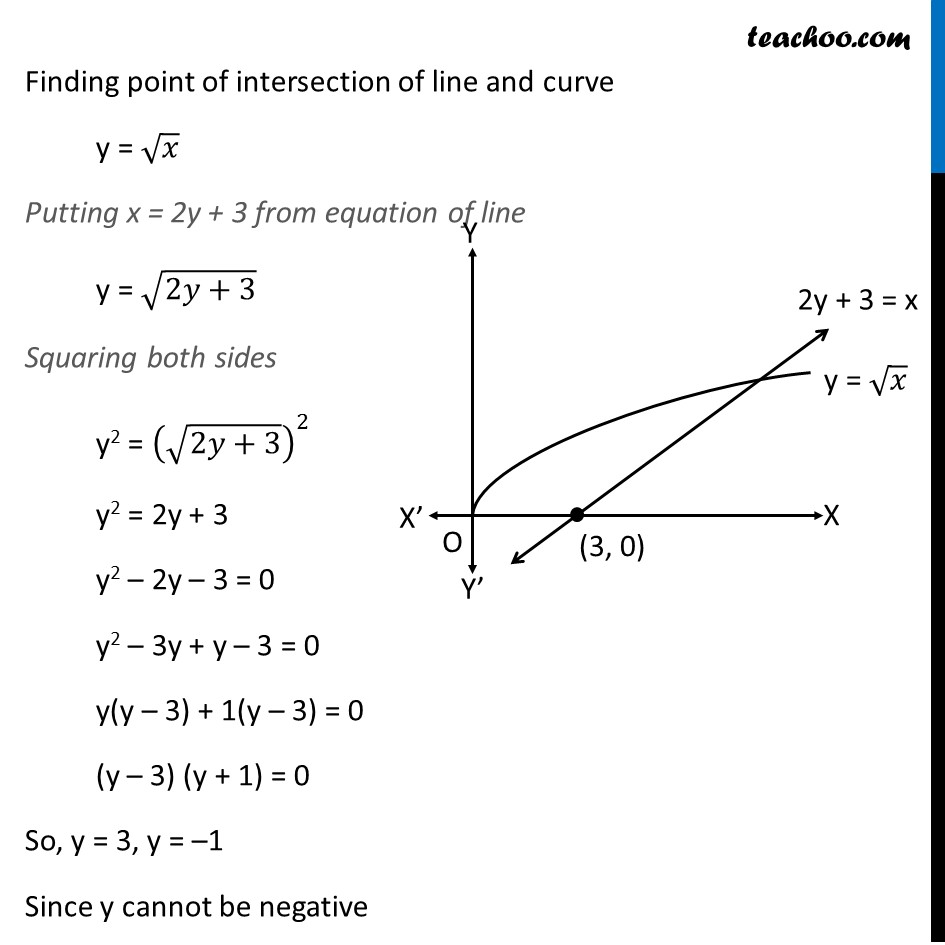
Find the area bounded by the curves y = √x, 2y + 3 = x and x axis


CBSE Class 12 Sample Paper for 2019 Boards
CBSE Class 12 Sample Paper for 2019 Boards
Last updated at Dec. 16, 2024 by Teachoo
Question 26 (OR 1 st question)
Find the area bounded by the curves y = √x, 2y + 3 = x and x axis







Transcript
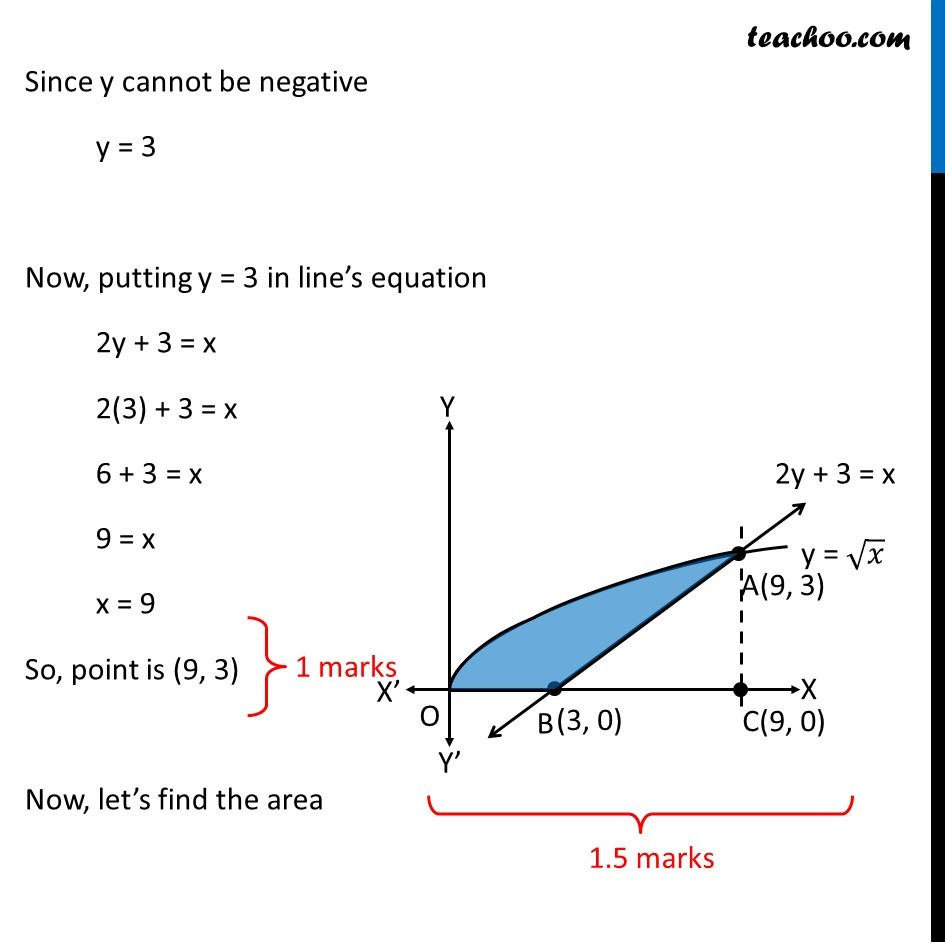
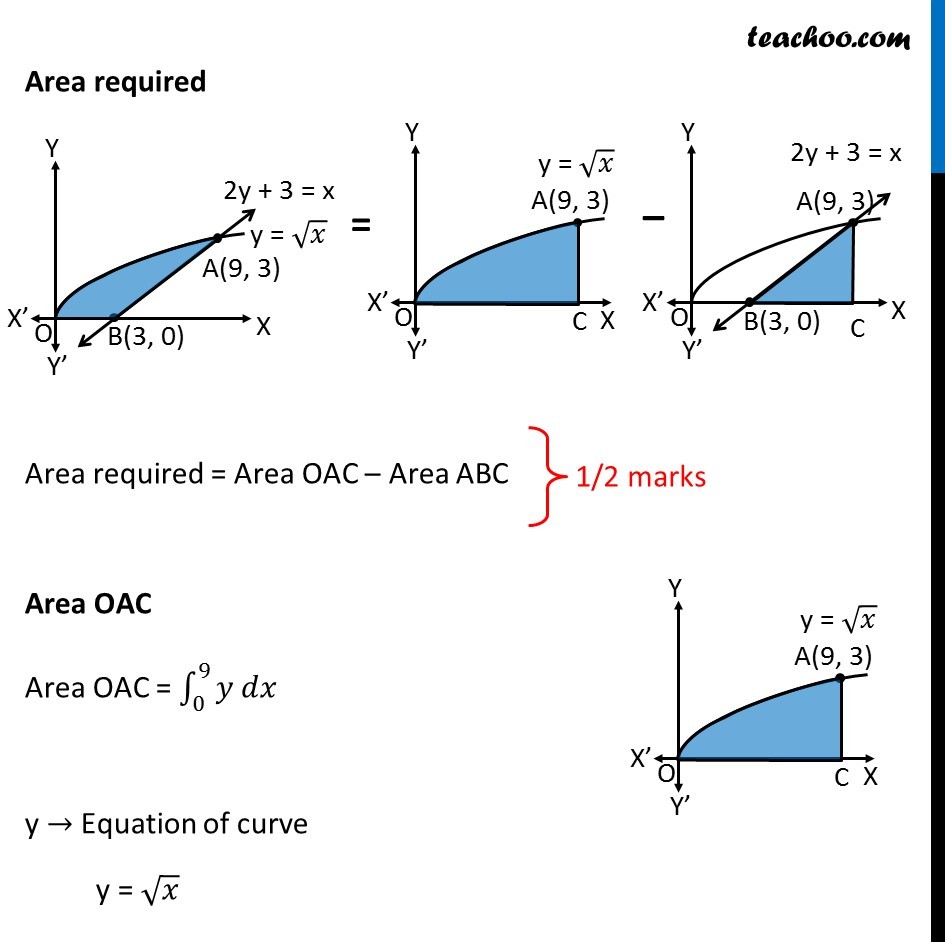
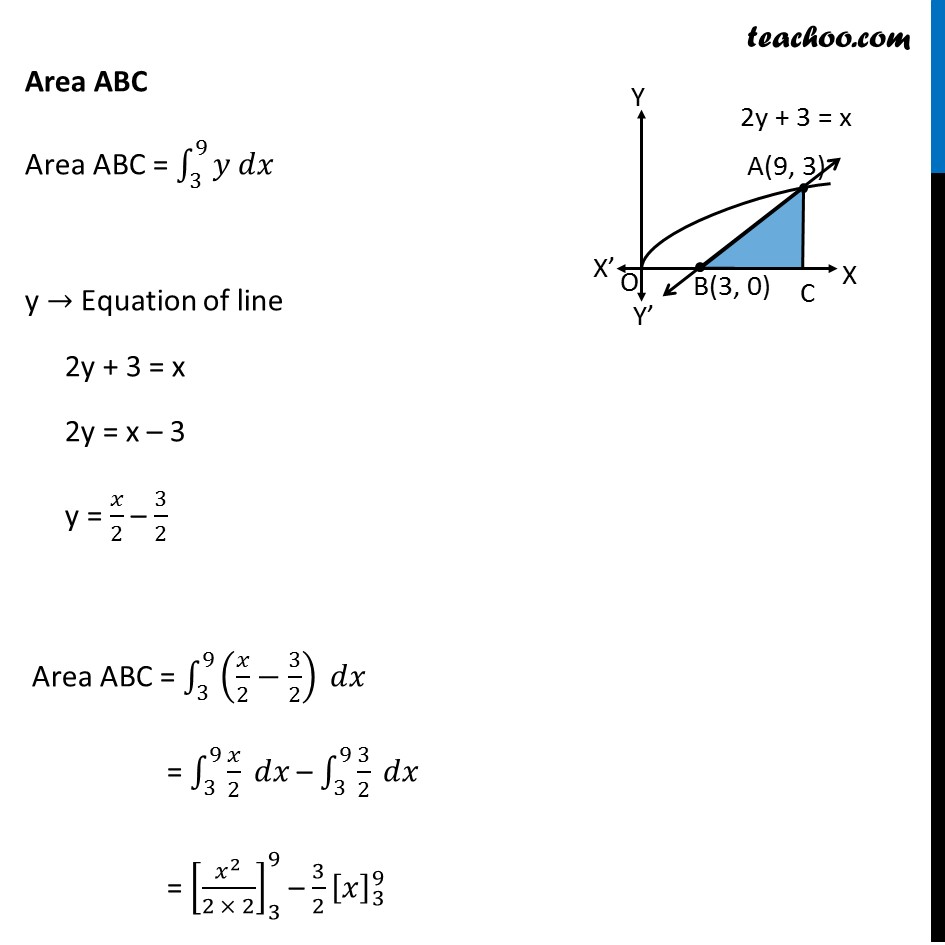
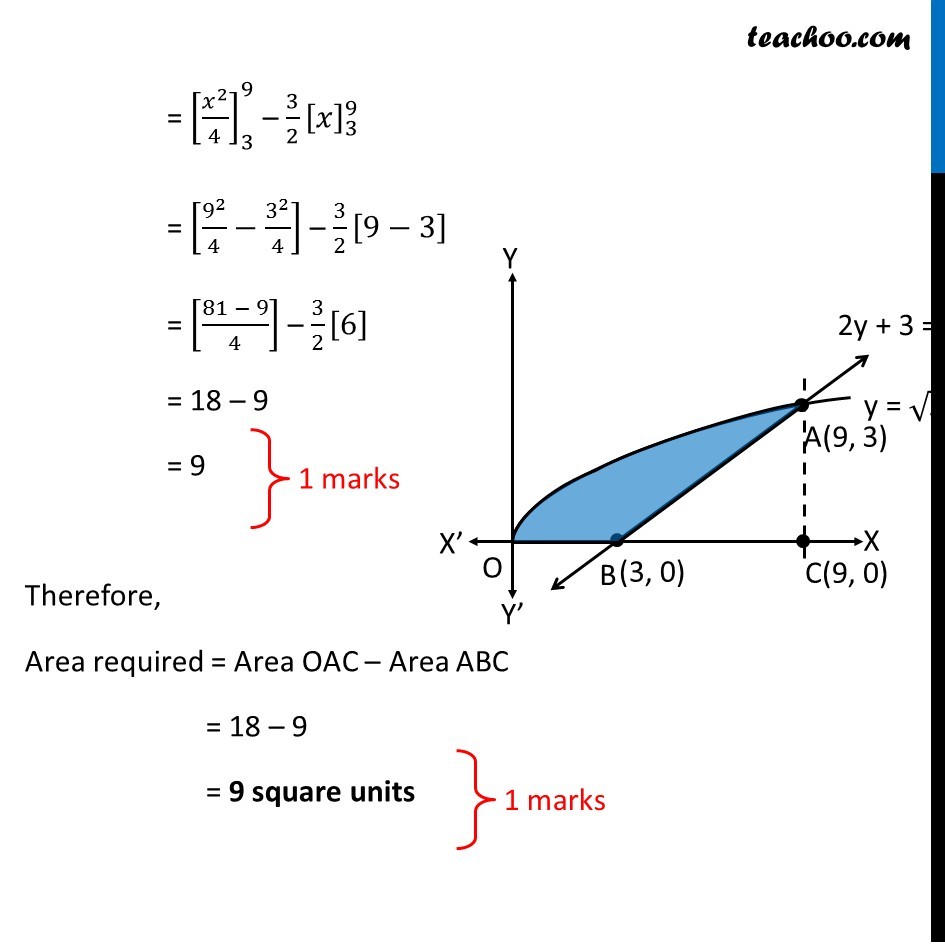
Question 26 (OR 1st question) Find the area bounded by the curves y = √𝑥, 2y + 3 = x and x axis Given equation of curves y = √𝑥 2y + 3 = x Here, y = √𝑥 y2 = x So, it is a parabola, with only positive values of y Drawing figure Drawing line 2y + 3 = x on the graph Finding point of intersection of line and curve y = √𝑥 Putting x = 2y + 3 from equation of line y = √(2𝑦+3) Squaring both sides y2 = (√(2𝑦+3))^2 y2 = 2y + 3 y2 – 2y – 3 = 0 y2 – 3y + y – 3 = 0 y(y – 3) + 1(y – 3) = 0 (y – 3) (y + 1) = 0 So, y = 3, y = –1 Since y cannot be negative y = 3 Since y cannot be negative y = 3 Now, putting y = 3 in line’s equation 2y + 3 = x 2(3) + 3 = x 6 + 3 = x 9 = x x = 9 So, point is (9, 3) Now, let’s find the area Area required Area required = Area OAC – Area ABC Area OAC Area OAC = ∫1_0^9▒〖𝑦 𝑑𝑥〗 y → Equation of curve y = √𝑥 Therefore, Area OAC = ∫1_0^9▒〖√𝑥 𝑑𝑥〗 = ∫1_0^9▒〖𝑥^(1/2) 𝑑𝑥〗 = [𝑥^(3/2)/(3/2)]_0^9 = 2/3 [9^(3/2)−0^(3/2) ] = 2/3 × 9^(3/2) = 2/3 × 3^((2 × 3/2) ) = 2/3 × 3^3 = 2 × 32 = 18 Area ABC Area ABC = ∫1_3^9▒〖𝑦 𝑑𝑥〗 y → Equation of line 2y + 3 = x 2y = x – 3 y = 𝑥/2 – 3/2 Area ABC = ∫1_3^9▒〖(𝑥/2−3/2) 𝑑𝑥〗 = ∫1_3^9▒〖𝑥/2 𝑑𝑥〗 – ∫1_3^9▒〖3/2 𝑑𝑥〗 = [𝑥^2/(2 × 2)]_3^9 – 3/2 [𝑥]_3^9 = [𝑥^2/4]_3^9 – 3/2 [𝑥]_3^9 = [9^2/4−3^2/4] – 3/2 [9−3] = [(81 − 9)/4] – 3/2 [6] = 18 – 9 = 9 Therefore, Area required = Area OAC – Area ABC = 18 – 9 = 9 square units