Misc 19 (MCQ) - Chapter 8 Class 12 Application of Integrals (Term 2)

Transcript

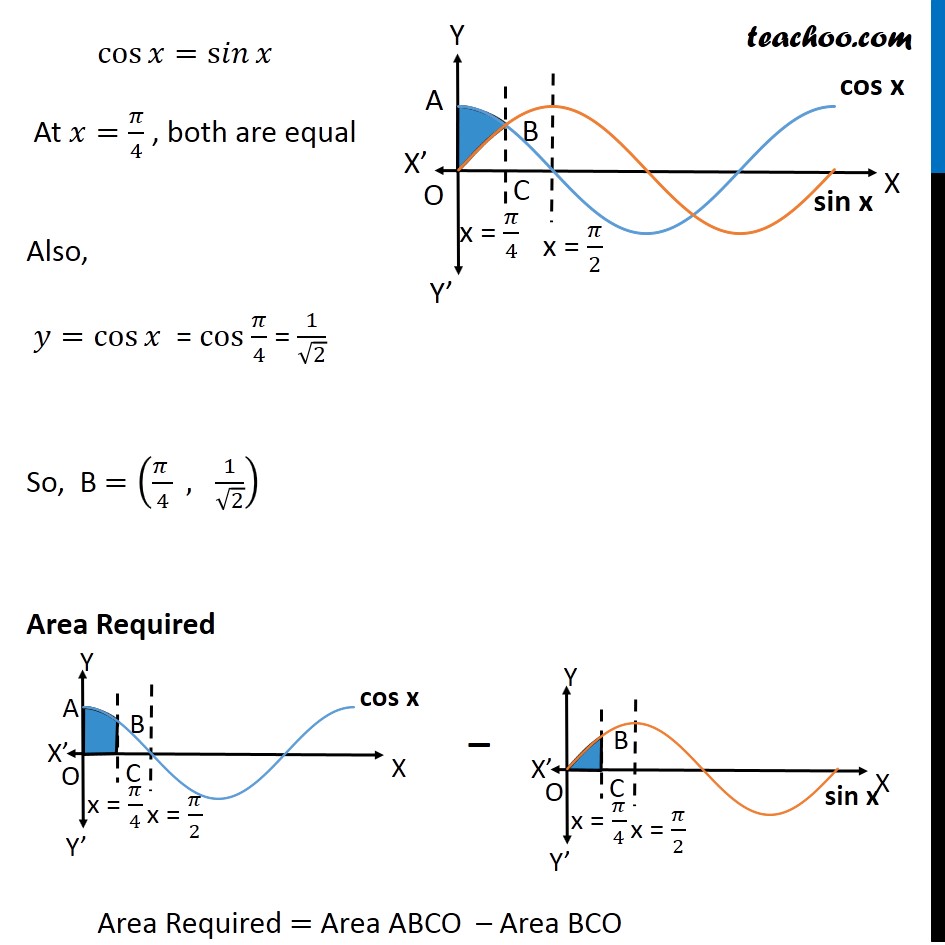
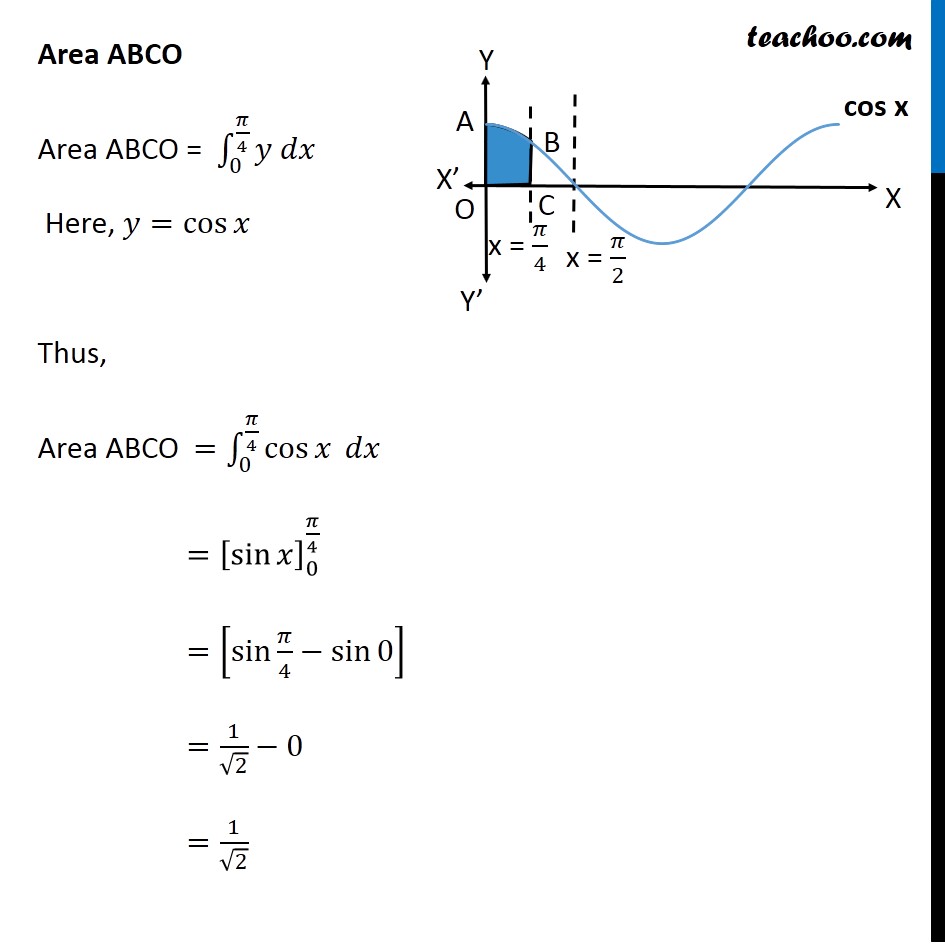
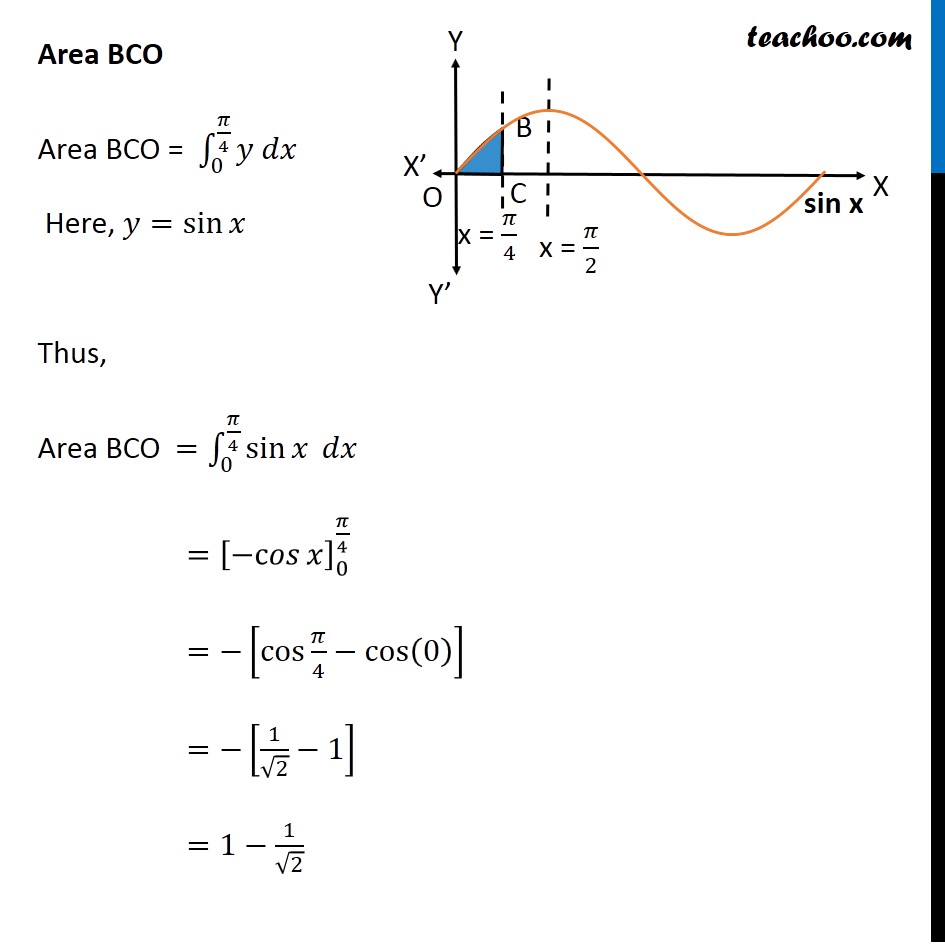
Misc 19 The area bounded by the 𝑦-axis, 𝑦=cos⁡𝑥 and 𝑦=sin⁡𝑥 when 0≤𝑥≤𝜋/2 is (A) 2 ( √("2 −1" )) (B) √("2 −1" ) (C) √("2 " )+1 (D) √("2 " ) Finding point of intersection B Solving 𝑦=cos⁡𝑥 and 𝑦=s𝑖𝑛⁡𝑥 cos⁡𝑥=s𝑖𝑛⁡𝑥 At 𝑥=𝜋/4 , both are equal Also, 𝑦=cos⁡𝑥 = cos 𝜋/4 = 1/√2 So, B =((𝜋 )/4 , 1/√2) Area Required Area Required = Area ABCO – Area BCO Area ABCO Area ABCO = ∫_0^(𝜋/4)▒〖𝑦 𝑑𝑥〗 Here, 𝑦=cos⁡𝑥 Thus, Area ABCO =∫_0^(𝜋/4)▒〖cos⁡𝑥 𝑑𝑥〗 =[sin⁡𝑥 ]_0^(𝜋/4) =[sin⁡〖𝜋/4−sin⁡0 〗 ] =1/√2−0 =1/√2 Area BCO Area BCO = ∫_0^(𝜋/4)▒〖𝑦 𝑑𝑥〗 Here, 𝑦=sin⁡𝑥 Thus, Area BCO =∫_0^(𝜋/4)▒〖sin⁡𝑥 𝑑𝑥〗 =[〖−c𝑜𝑠〗⁡𝑥 ]_0^(𝜋/4) =−[cos⁡〖𝜋/4−cos⁡(0) 〗 ] =−[1/√2−1] =1−1/√2 Therefore Area Required = Area ABCO – Area BCO =1/√2−[1−1/√2] =1/√2+1/√2−1 =2/√2−1 =√𝟐−𝟏 ∴ Option B is Correct