Misc 18 - Chapter 8 Class 12 Application of Integrals

Transcript

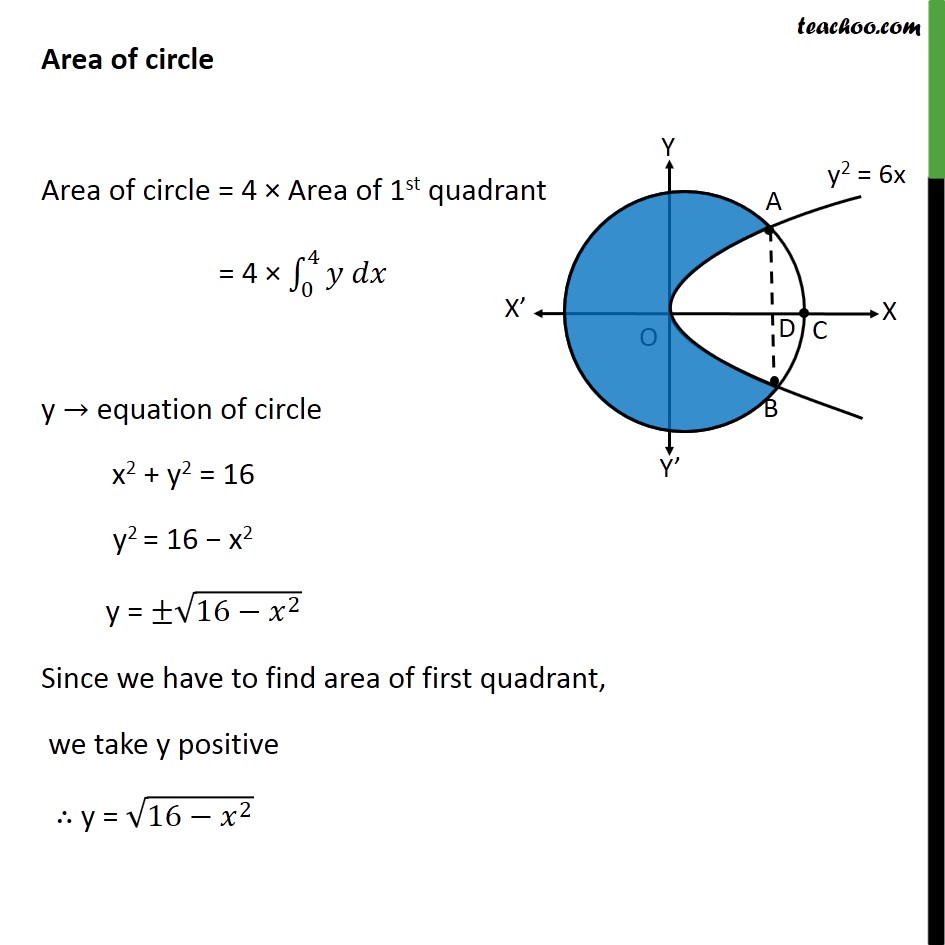
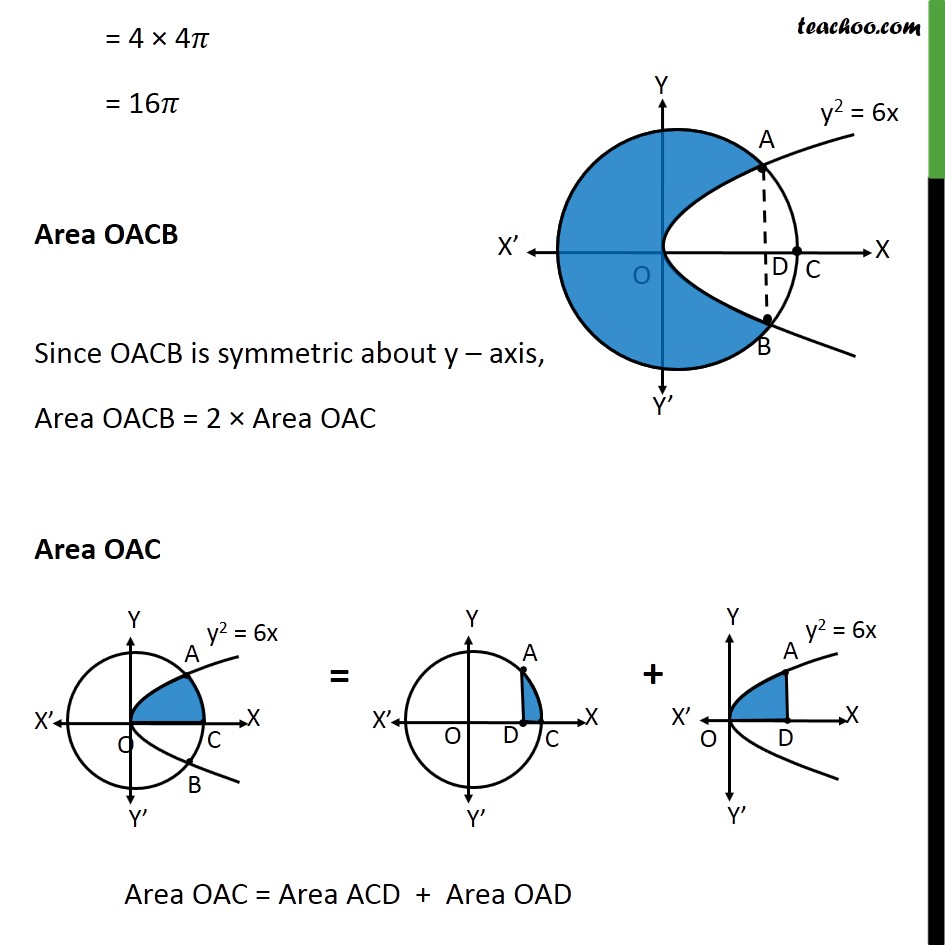
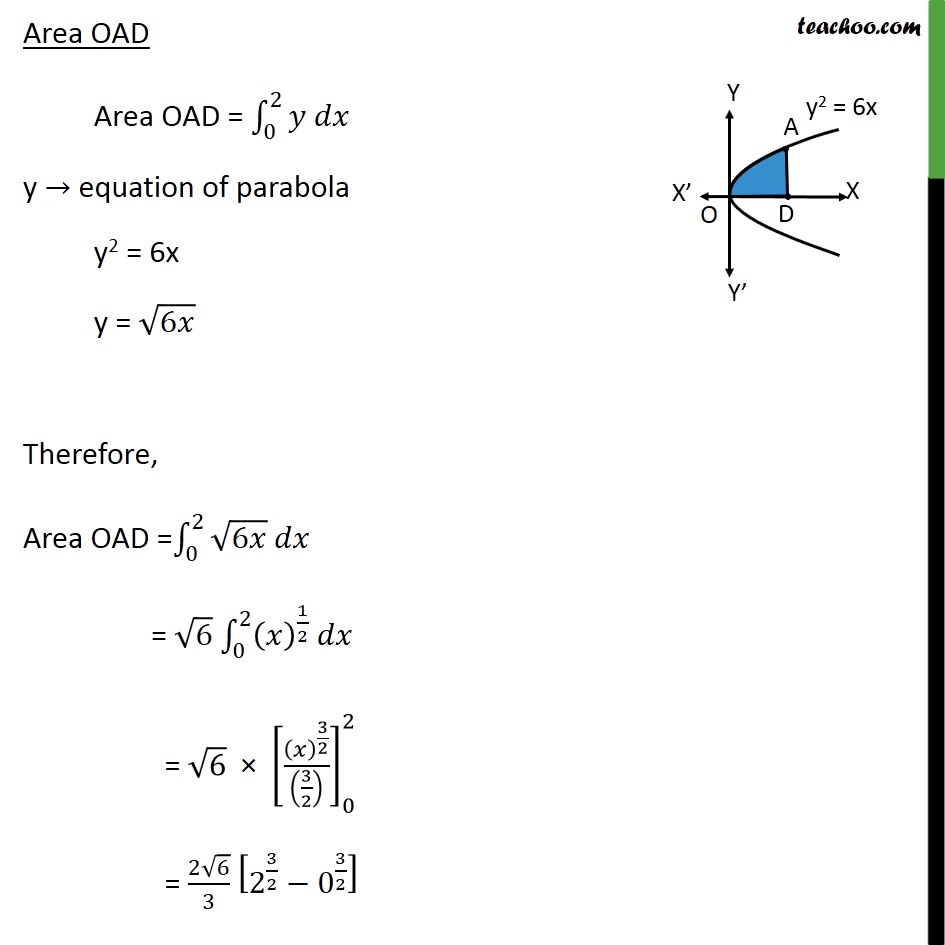
Misc 18 The area of the circle 𝑥2+𝑦2 = 16 exterior to the parabola 𝑦2=6𝑥 is (A) 4﷮3﷯ (4𝜋− ﷮3﷯ ) (B) 4﷮3﷯ (4𝜋+ ﷮3﷯) (C) 4﷮3﷯ (8𝜋− ﷮3﷯) (D) 4﷮3﷯ (8𝜋+ ﷮3﷯) Step 1: Draw the Figure 𝑥2+𝑦2 = 16 𝑥2+𝑦2= 4﷮2﷯ It is a circle with center 0 , 0﷯ & radius 4 And y2 = 6x is a parabola Step 2: Finding point of intersection A & B Solving 𝑦﷮2﷯=6𝑥 …(1) & 𝑥2+ 𝑦2=16 …(2) Putting (1) in (2) 𝑥2+ 𝑦2=16 𝑥2+6𝑥=16 𝑥2+6𝑥−16=0 𝑥2+8𝑥−2𝑥−16=0 𝑥(𝑥+8) −2(𝑥+8)=0 𝑥−2﷯ 𝑥+8﷯=0 So, 𝑥=2 & 𝑥=−8 Area of circle Area of circle = 4 × Area of 1st quadrant = 4 × 0﷮4﷮𝑦 𝑑𝑥﷯ y → equation of circle x2 + y2 = 16 y2 = 16 − x2 y = ± ﷮16− 𝑥﷮2﷯﷯ Since we have to find area of first quadrant, we take y positive ∴ y = ﷮16− 𝑥﷮2﷯﷯ Therefore Area of circle = 4 × 0﷮4﷮ ﷮16− 𝑥﷮2﷯﷯﷯𝑑𝑥 = 4 × 0﷮4﷮ ﷮ 4﷮2﷯− 𝑥﷮2﷯﷯﷯𝑑𝑥 = 4 × 𝑥﷮2﷯ ﷮ 4﷮2﷯− 𝑥﷮2﷯﷯+ 4﷮2﷯﷮2﷯ sin﷮−1﷯﷮ 𝑥﷮4﷯﷯﷯﷮0﷮4﷯ = 4 × 𝑥﷮2﷯ ﷮16− 𝑥﷮2﷯﷯+8 sin﷮−1﷯﷮ 𝑥﷮4﷯﷯﷯﷮0﷮4﷯ = 4 × 4﷮2﷯ ﷮16− 4﷮2﷯﷯+8 sin﷮−1﷯﷮ 4﷮4﷯﷯﷯− 0﷮2﷯ ﷮16− 0﷮2﷯﷯+8 sin﷮−1﷯﷮ 0﷮4﷯﷯﷯﷯﷯ = 4 × 0+8 sin﷮−1﷯﷮1−0−8 sin﷮−1﷯﷮0﷯﷯﷯ = 4 × 0+8× 𝜋﷮2﷯−0−0﷯ = 4 × 4𝜋 = 16𝜋 Area OACB Since OACB is symmetric about y – axis, Area OACB = 2 × Area OAC Area OAC Area ACD Area ACD = 2﷮4﷮𝑦 𝑑𝑥﷯ y → equation of circle x2 + y2 = 16 y2 = 16 − x2 y = ± ﷮16 − x2 ﷯ Since ACD is 1st quadrant y = ﷮16− 𝑥﷮2﷯﷯ Therefore, Area ACD = 2﷮4﷮ ﷮16− 𝑥﷮2﷯﷯ 𝑑𝑥﷯ = 2﷮4﷮ ﷮ 4﷮2﷯− 𝑥﷮2﷯﷯ ﷯ = 2﷮4﷮ ﷮ 4﷮2﷯− 𝑥﷮2﷯﷯ ﷯ = 𝑥﷮2﷯ ﷮ 4﷮2﷯− 𝑥﷮2﷯﷯+ 4﷮2﷯﷮4﷯ sin﷮−1﷯﷮ 𝑥﷮4﷯﷯﷯﷮2﷮4﷯ = 𝑥﷮2﷯ ﷮16− 𝑥﷮2﷯﷯+8 sin﷮−1﷯﷮ 𝑥﷮4﷯﷯﷯﷮2﷮4﷯ = 4﷮2﷯ ﷮16− 4﷮2﷯﷯+8 sin﷮−1﷯﷮ 4﷮4﷯﷯﷯ − 2﷮2﷯ ﷮16− 2﷮2﷯﷯+8 sin﷮−1﷯﷮ 2﷮4﷯﷯﷯ = 8 × 𝜋﷮2﷯ − 2 ﷮3﷯ − 8 × 𝜋﷮6﷯ = 4𝜋 − 4𝜋﷮3﷯ − 2 ﷮3﷯ = 8𝜋﷮3﷯ − 2 ﷮3﷯ Area OAD Area OAD = 0﷮2﷮𝑦 𝑑𝑥﷯ y → equation of parabola y2 = 6x y = ﷮6𝑥﷯ Therefore, Area OAD = 0﷮2﷮ ﷮6𝑥﷯ 𝑑𝑥﷯ = ﷮6﷯ 0﷮2﷮ 𝑥﷯﷮ 1﷮2﷯﷯ 𝑑𝑥﷯ = ﷮6﷯ × 𝑥﷯﷮ 3﷮2﷯﷯﷮ 3﷮2﷯﷯﷯﷯﷮0﷮2﷯ = 2 ﷮6﷯﷮3﷯ 2﷮ 3﷮2﷯﷯− 0﷮ 3﷮2﷯﷯﷯ = 2 ﷮6﷯﷮3﷯ × 2 ﷮2﷯ = 4 ﷮2﷯× ﷮3﷯× ﷮2﷯﷮3﷯ = 8 ﷮3﷯﷮3﷯ Area OAC = Area ACD + Area OAD = 8𝜋﷮3﷯−2 ﷮3﷯+ 8﷮3﷯ ﷮3﷯ = 8𝜋﷮3﷯+ 2﷮3﷯ ﷮3﷯ Thus, Area OACB = 2 × Area OAC = 2 × 8𝜋﷮3﷯+ 2 ﷮3﷯﷮3﷯﷯ = 16𝜋﷮3﷯+ 4 ﷮3﷯﷮3﷯ Therefore, Required Area = Area of circle − Area OACB = 16𝜋 − 4 ﷮3﷯﷮3﷯+ 16﷮3﷯𝜋﷯ = 32𝜋﷮3﷯− 4 ﷮3﷯﷮3﷯ = 4﷮3﷯(8𝜋 − ﷮3﷯) square units. So, C is the correct answer