Ex 8.1, 4 - Chapter 8 Class 12 Application of Integrals (Term 2)

Transcript

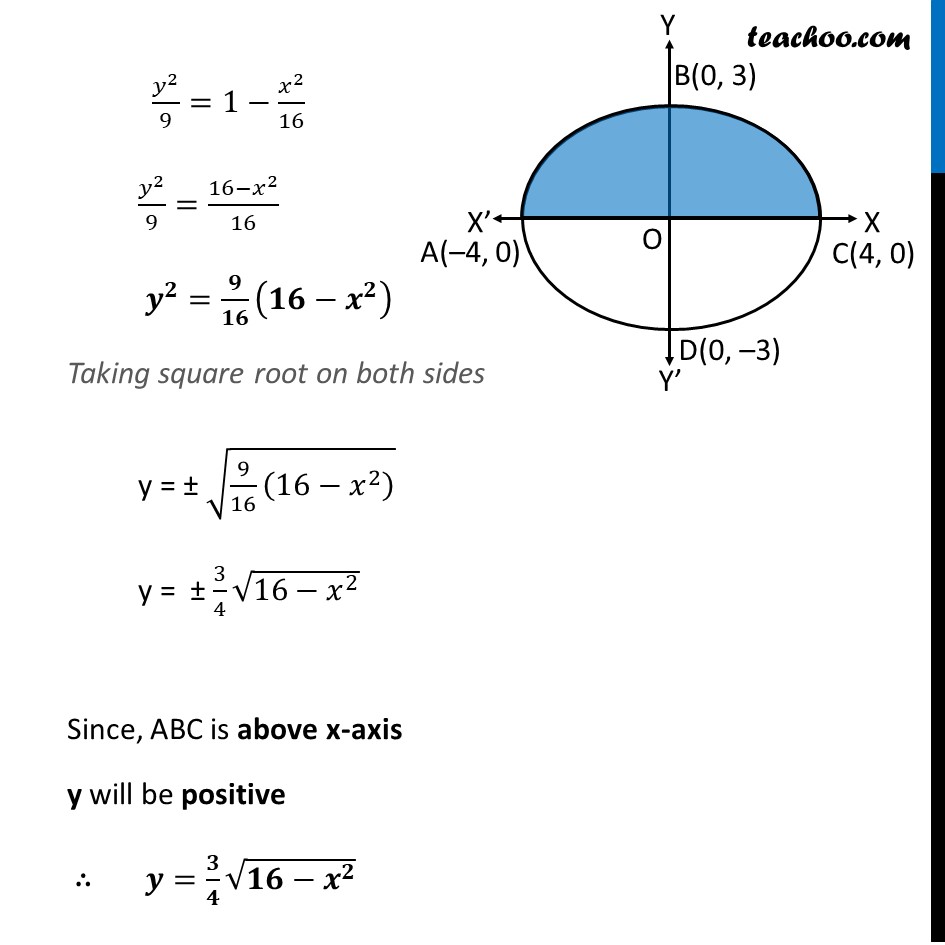
Ex 8.1, 4 Find the area of the region bounded by the ellipse 𝑥﷮2﷯﷮16﷯+ 𝑦﷮2﷯﷮9﷯=1 Equation Of Given Ellipse is :- 𝑥﷮2﷯﷮16﷯+ 𝑦﷮2﷯﷮9﷯=1 𝑥﷮2﷯﷮ 4﷯﷮2﷯﷯+ 𝑦﷮2﷯﷮ 3﷯﷮2﷯﷯=1 Area of ellipse = Area of ABCD = 2 × [Area Of ABC] = 2 × −4﷮4﷮𝑦.﷯𝑑𝑥 Finding y We know that 𝑥﷮2﷯﷮16﷯+ 𝑦﷮2﷯﷮9﷯=1 𝑦﷮2﷯﷮9﷯=1− 𝑥﷮2﷯﷮16﷯ 𝑦﷮2﷯﷮9﷯= 16− 𝑥﷮2﷯﷮16﷯ 𝑦﷮2﷯= 9﷮16﷯ 16− 𝑥﷮2﷯﷯ Taking square root on both sides y = ± ﷮ 9﷮16﷯ 16− 𝑥﷮2﷯﷯﷯ y = ± 3﷮4﷯ ﷮16− 𝑥﷮2﷯﷯ Since , ABC is above x-axis y will be positive ∴ 𝑦= 3﷮4﷯ ﷮16− 𝑥﷮2﷯﷯ Now, Area of ellipse = 2 × −4﷮4﷮𝑦.﷯𝑑𝑥 = 2 × −4﷮4﷮ 3﷮4﷯ ﷮16− 𝑥﷮2﷯﷯﷯𝑑𝑥 = 2 × 3﷮4﷯ −4﷮4﷮ ﷮16− 𝑥﷮2﷯﷯﷯𝑑𝑥 = 3﷮2﷯ −4﷮4﷮ ﷮ 4﷯﷮2﷯− 𝑥﷮2﷯﷯﷯𝑑𝑥 = 3﷮2﷯ 𝑥﷮2﷯ ﷮ 4﷯﷮2﷯− 𝑥﷮2﷯﷯+ 4﷯﷮2﷯﷮2﷯ sin﷮−1﷯﷮ 𝑥﷮4﷯﷯﷯﷮−4﷮4﷯ = 3﷮2﷯ 4﷮2﷯ ﷮ 4﷯﷮2﷯− 4﷯﷮2﷯﷯− −4﷯﷮2﷯ ﷮ 4﷯﷮2﷯− −4﷯﷮2﷯﷯+ 16﷮2﷯ sin﷮−1﷯﷮ 4﷮4﷯﷯− 16﷮2﷯﷯ sin﷮−1﷯ −4﷮4﷯﷯﷯ = 3﷮2﷯ 2 0﷯+2 0﷯+8 sin﷮−1﷯(1)﷮− 8 sin﷮−1﷯﷮ −1﷯﷯﷯﷯ = 3﷮2﷯ 0+8 sin﷮−1﷯﷮ 1﷯−8 𝒔𝒊𝒏﷮−𝟏﷯﷮ −𝟏﷯﷯﷯﷯ = 3﷮2﷯ 8 sin﷮−1﷯﷮ 1﷯−8(− 𝒔𝒊𝒏﷮−𝟏﷯﷮ 𝟏﷯﷯)﷯﷯ = 3﷮2﷯ 8 sin﷮−1﷯﷮ 1﷯+8 sin﷮−1﷯﷮ 1﷯﷯﷯﷯ = 3﷮2﷯ ×16 sin﷮−1﷯﷮ 1﷯﷯ = 3 × 8 × 𝜋﷮2﷯ = 12π ∴ Area of Ellipse = 12π Square units