Check sibling questions

Question 7 - Ex 8.1 - Chapter 8 Class 12 Application of Integrals

Last updated at May 29, 2023 by

Ex 8.1, 9 - Find area bounded by parabola y = x2 and y = |x| - Area between curve and line

Ex 8.1, 9 - Chapter 8 Class 12 Application of Integrals - Part 2
Ex 8.1, 9 - Chapter 8 Class 12 Application of Integrals - Part 3 Ex 8.1, 9 - Chapter 8 Class 12 Application of Integrals - Part 4

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

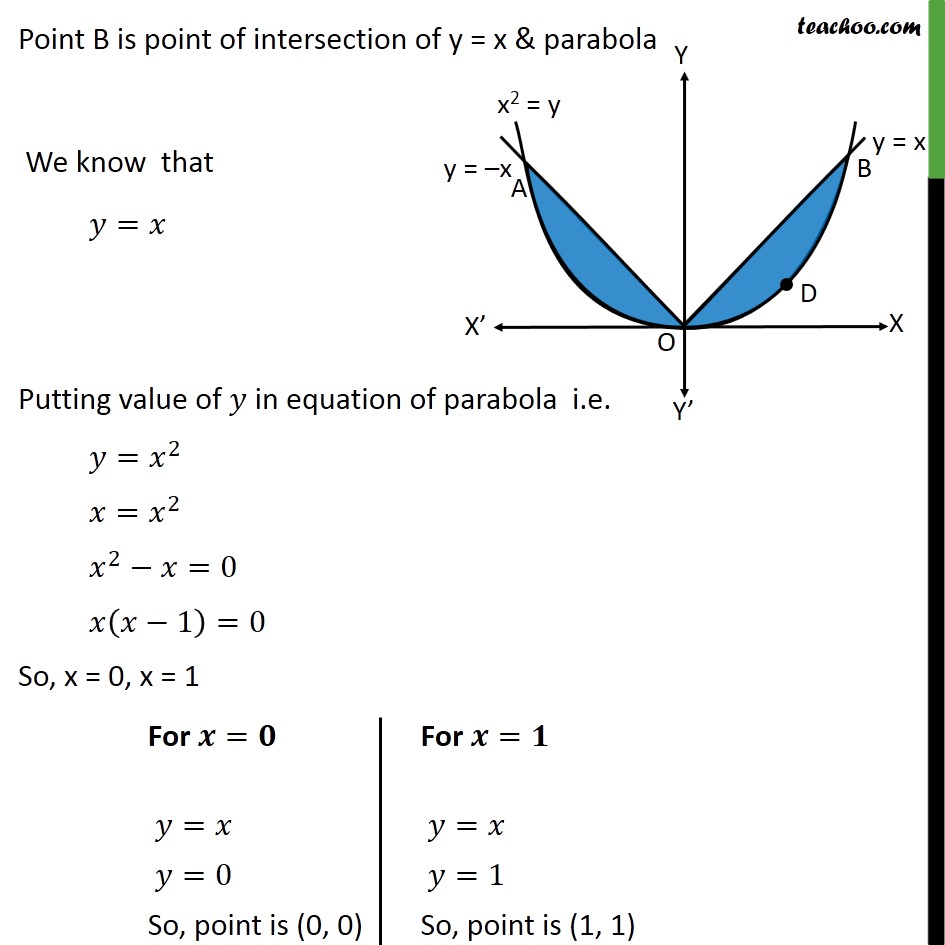
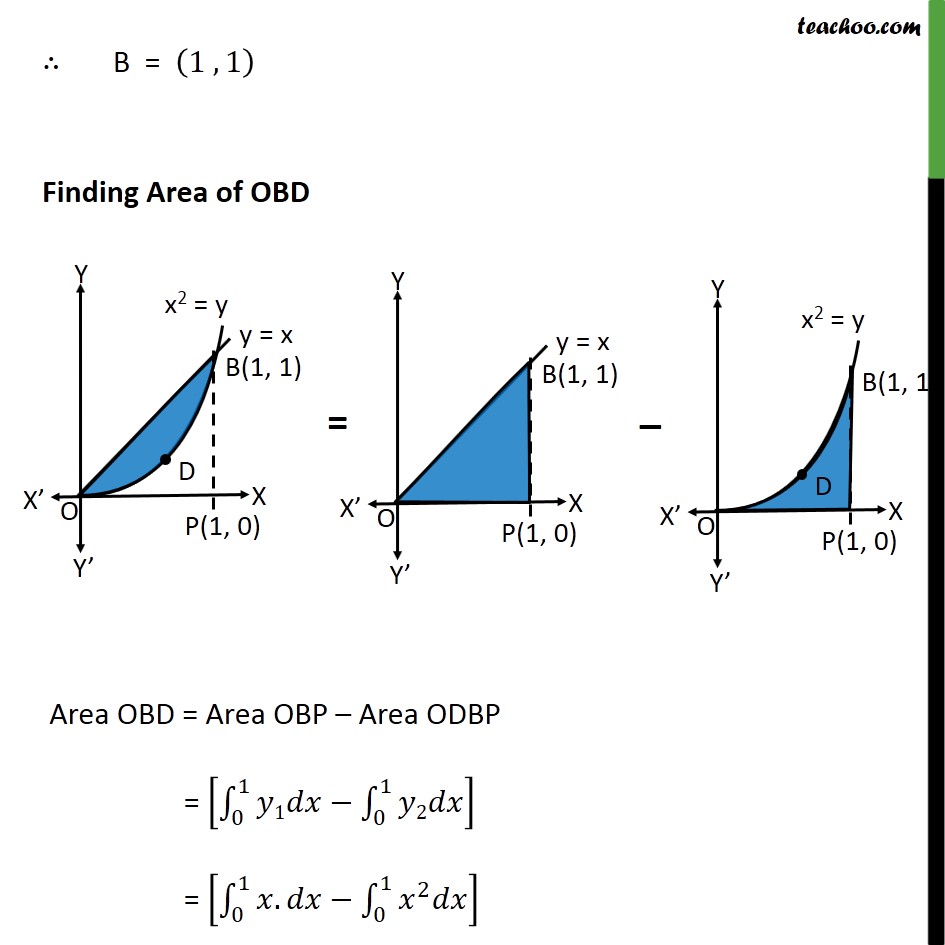
Question 7 Find the area of the region bounded by the parabola = 2 and = We know = & , <0 & , 0 Let OA represent the line = & OB represent the line = Since parabola is symmetric about its axis, x2 = y is symmetric about y axis Area of shaded region = 2 (Area of OBD) First, we find Point B, Point B is point of intersection of y = x & parabola We know that = Putting value of in equation of parabola i.e. = 2 = 2 2 =0 1 =0 So, x = 0, x = 1 B = 1 , 1 Finding Area of OBD Area OBD = Area OBP Area ODBP = 0 1 1 0 1 2 = 0 1 . 0 1 2 Area of shaded region = 2 (Area of OBD) = 2 0 1 . 0 1 2 = 2 2 2 0 1 3 3 0 1 = 2 1 0 2 1 0 3 = 2 1 2 1 3 = 2 3 2 6 = 1 3 Required Area = square units

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.