


Miscellaneous
Misc 1 (ii) Important
Misc 2 Important
Misc 3 Important
Misc 4 (MCQ)
Misc 5 (MCQ) Important
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Important Deleted for CBSE Board 2024 Exams
Question 4 Deleted for CBSE Board 2024 Exams
Question 5 Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams
Question 8 Important Deleted for CBSE Board 2024 Exams
Question 9 Important Deleted for CBSE Board 2024 Exams You are here
Question 10 Deleted for CBSE Board 2024 Exams
Question 11 Important Deleted for CBSE Board 2024 Exams
Question 12 Deleted for CBSE Board 2024 Exams
Question 13 (MCQ) Deleted for CBSE Board 2024 Exams
Question 14 (MCQ) Important Deleted for CBSE Board 2024 Exams
Miscellaneous
Last updated at April 16, 2024 by Teachoo






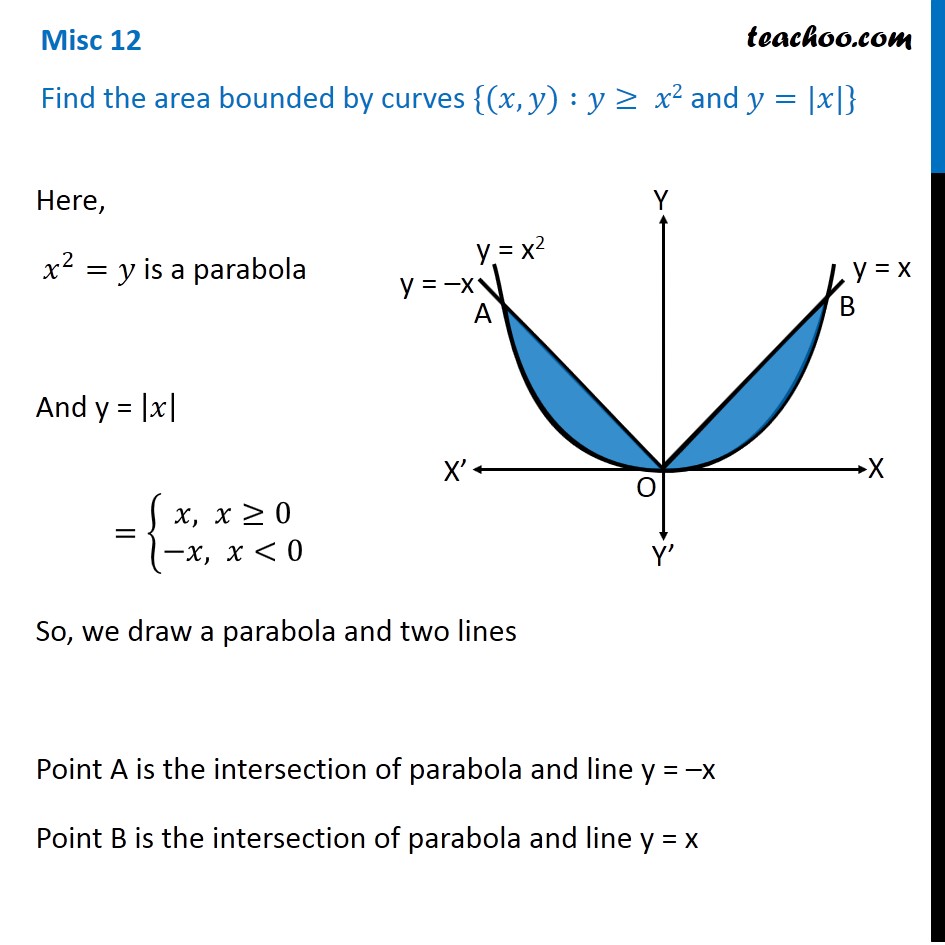
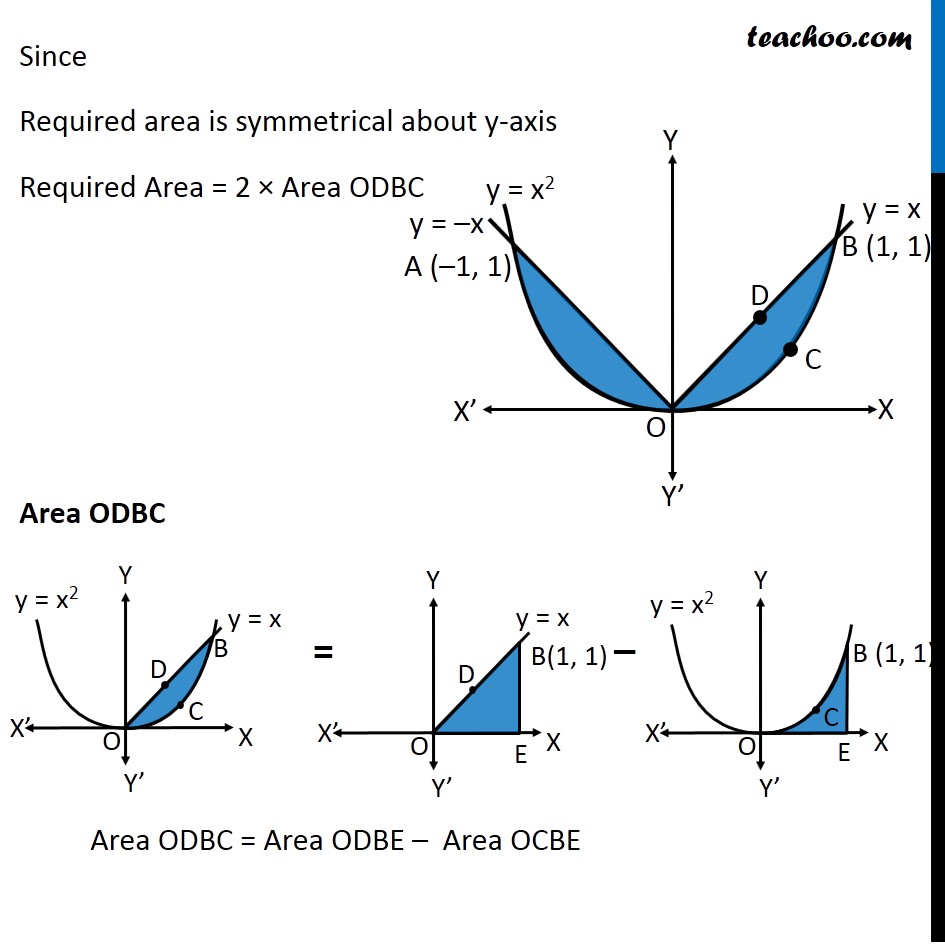
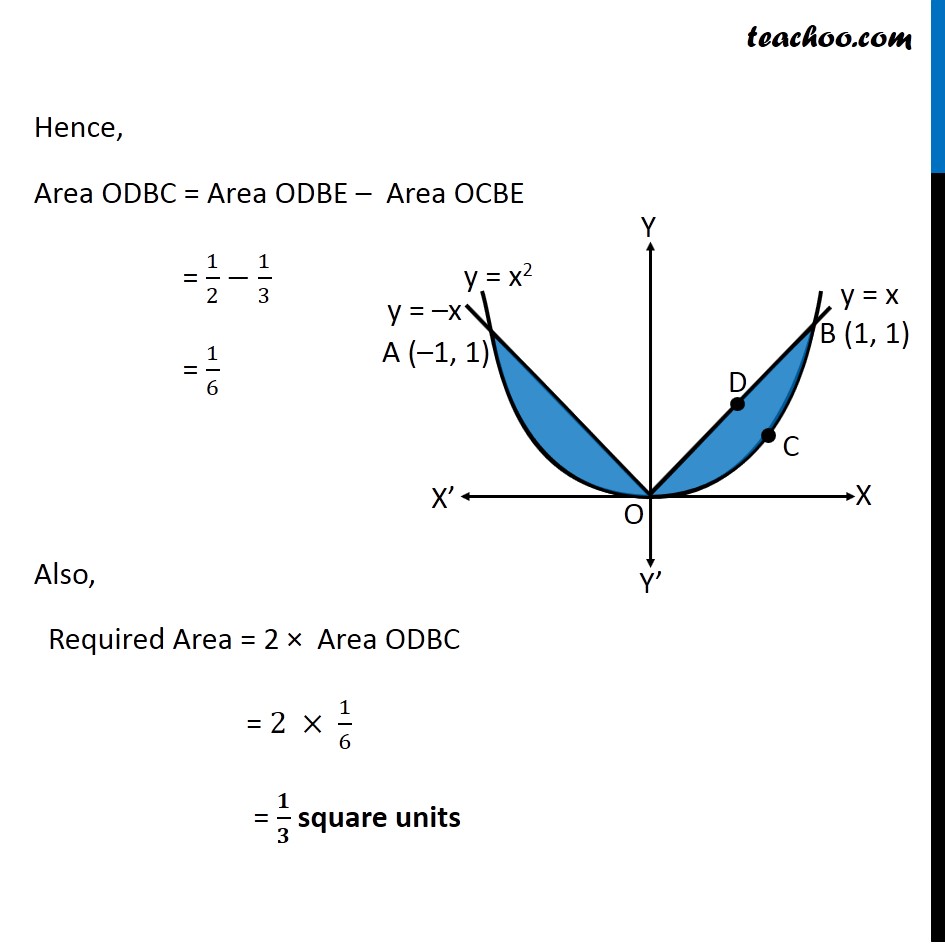
Question 9 Find the area bounded by curves {(𝑥, 𝑦) :𝑦≥ 𝑥2 and 𝑦=|𝑥|} Here, 𝑥^2=𝑦 is a parabola And y = |𝑥| ={█(𝑥, 𝑥≥0@&−𝑥, 𝑥<0)┤ So, we draw a parabola and two lines Point A is the intersection of parabola and line y = –x Point B is the intersection of parabola and line y = x Finding points A & B Point A Point A is intersection of y = x2 & y = –x Solving x2 = –x x2 + x = 0 x(x + 1) = 0 So, x = –1 & x = 0 For x = –1 y = –x = –(–1) = 1 So, point A (–1, 1) Point B Point B is intersection of y = x2 & y = x Solving x2 = x x2 – x = 0 x(x – 1) = 0 So, x = 1 & x = 0 For x = 1 y = x = 1 So, point B (1, 1) Since Required area is symmetrical about y-axis Required Area = 2 × Area ODBC Area ODBC Area ODBC = Area ODBE – Area OCBE Area ODBE Area ODBE = ∫_0^1▒〖𝑦 𝑑𝑥〗 y → Equation of line y = x Area ODBE =∫_0^1▒〖𝑥 𝑑𝑥〗 =[𝑥^2/2]_0^1 =1^2/( 2)−0^2/2 =1/2 Area OCBE Area OCBE = ∫_0^1▒〖𝑦 𝑑𝑥〗 y → Equation of parabola y = x2 Therefore, Area OCBE =∫_0^1▒〖𝑥^2 𝑑𝑥〗 =[𝑥^3/3]_0^1 =1^3/3−0^3/3 =1/3 Hence, Area ODBC = Area ODBE – Area OCBE = 1/2−1/3 = 1/6 Also, Required Area = 2 × Area ODBC = 2 × 1/6 = 𝟏/𝟑 square units