Example 28 - Chapter 4 Class 12 Determinants

Transcript

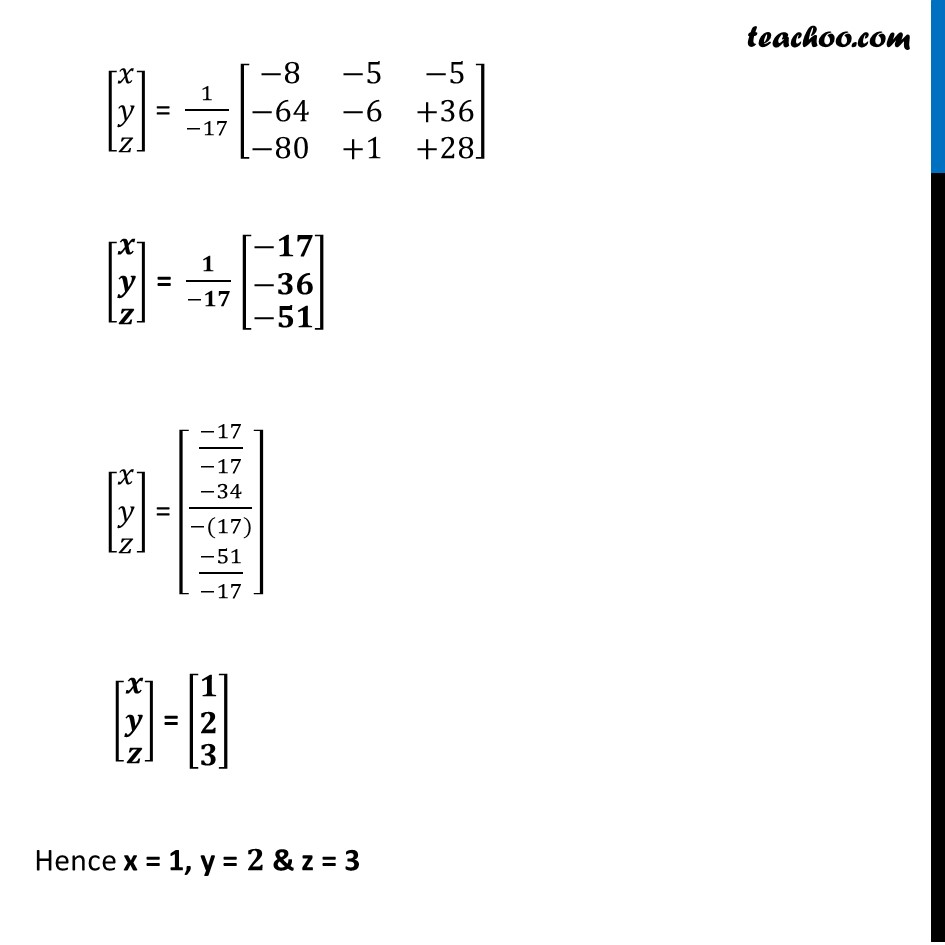
Example 28 Solve the following system of equations by matrix method. 3x – 2y + 3z = 8 2x + y – z = 1 4x – 3y + 2z = 4 The system of equation is 3x – 2y + 3z = 8 2x + y – z = 1 4x – 3y + 2z = 4 Writing equation as AX = B [■8(3&−2&3@2&1&−1@4&−3&2)][■8(𝑥@𝑦@𝑧)] = [■8(8@1@4)] Hence A = [■8(3&−2&3@2&1&−1@4&−3&2)], 𝑥= [■8(𝑥@𝑦@𝑧)] & B = [■8(8@1@4)] Calculating |A| |A| = |■8(3&−2&3@2&1&−1@4&−3&2)| = 3 |■8(1&−1@−3&2)| – 1( – 2) |■8(2&−1@4&2)| + 3 |■8(2&1@4&−3)| = 3 (2 – 3) – 2 (4 + 4) + 3 (–6 – 4) = 3 (–1) + 2(8) + 3 (–10) = –3 + 16 – 30 = –17 Since, |A| ≠ 0 ∴ System of equation is consistent & has a unique solution Now, AX = B X = A-1 B Calculating A-1 A-1 = 1/(|A|) adj (A) adj (A) = [■8(A_11&A_12&A_13@A_21&A_22&A_23@A_31&A_32&A_33 )]^′ = [■8(A_11&A_21&A_13@A_12&A_22&A_23@A_13&A_32&A_33 )] A = [■8(3&−2&3@2&1&−1@4&−3&2)] M11 = |■8(1&−1@−3&2)| = 2 – 3 = –1 M12 = |■8(2&−1@4&2)| = 4 + 4 = 8 M13 = |■8(2&1@4&−3)| = –6 – 4 = –10 M21 = |■8(−2&3@−3&2)| = –4 + 9 = 5 M22 = |■8(3&3@4&2)| = 6 – 12 = – 6 M23 = |■8(3&−2@4&−3)| = –9 + 8 = –1 M31 = |■8(−2&3@1&−1)| = 1 – 2 = –1 M32 = |■8(3&3@2&−1)| = –3 – 6 = –9 M33 = |■8(3&−2@2&1)| = 3 + 4 = 7 Now, A11 = (–1)1+1 . M11 = (–1)2 . (–1) = –1 A12 = (–1)1+2 . M12 = (–1)3 . 8 = –8 A13 = (–1)1+3 . M13 = (–1)4 . ( –10) = –10 A21 = (–1)2+1 . M21 = (–1)3 . (5) = –5 A22 = (–1)2+2 . M22 = (–1)4 . (–6) = –6 A23 = (–1)2+3 . ( – 1) = (–1)5 . (–1) = 1 A31 = (–1)3+1 . M31 = (–1)4 . (–1) = –1 A32 = (–1)3+2 . M32 = (–1)5 . (–9) = 9 A33 = (–1)3+3 . M33 = (–1)6 . 7 = 7 Thus, adj (A) =[■8(−1&−5&−1@−8&−6&9@−10&1&7)] Now, A-1 = 1/(|A|) adj A Putting values = 1/(−17) [■8(−1&−5&−1@−8&−6&9@−10&1&7)] Also, X = A-1 B Putting values [█(■8(𝑥@𝑦)@𝑧)] = 1/(−17) [■8(−1&−5&−1@−8&−6&9@−10&1&7)][█(■8(8@1)@4)] [█(■8(𝑥@𝑦)@𝑧)] = 1/(−17) [■8(−1(8)+(−5)(1)+(−1)4@−8(8)+(−6)(1)+9(4)@−10(8)+1(1)+7(4) )] [█(■8(𝑥@𝑦)@𝑧)] = 1/(−17) [■8(−8&−5&−5@−64&−6&+36@−80&+1&+28)] [█(■8(𝑥@𝑦)@𝑧)] = 1/(−17) [█(■8(−17@−36)@−51)] [█(■8(𝑥@𝑦)@𝑧)] = [█(■8((−17)/(−17)@(−34)/(−(17)))@(−51)/(−17))] [█(■8(𝑥@𝑦)@𝑧)] = [█(■8(1@2)@3)] Hence x = 1, y = 𝟐 & z = 3