Ex 9.3, 16 - Chapter 9 Class 11 Straight Lines

Transcript

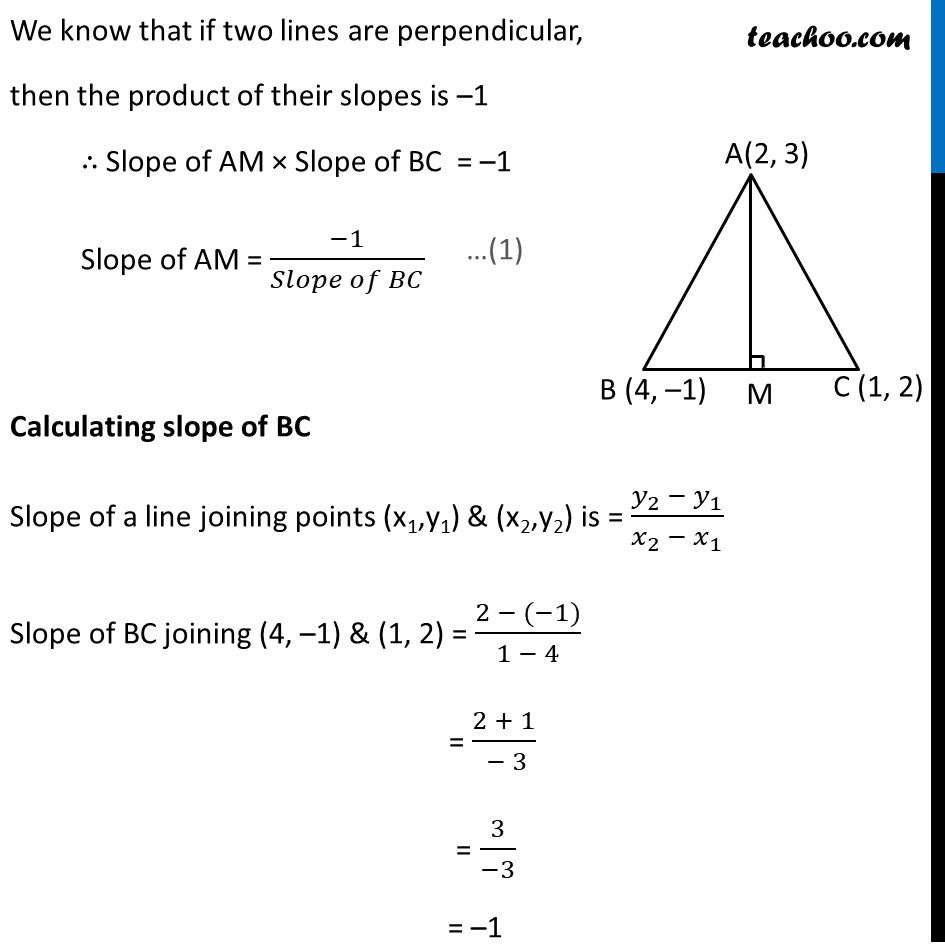
Ex 9.3, 16 In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A. Let ABC be the triangle with vertex A(2, 3), B(4, –1) & C(1, 2) & AM be the altitude of triangle ABC We need to calculate length & equation of altitude AM Now, Altitude AM is perpendicular to BC We know that if two lines are perpendicular, then the product of their slopes is –1 ∴ Slope of AM × Slope of BC = –1 Slope of AM = (−1)/(𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐵𝐶) Calculating slope of BC Slope of a line joining points (x1,y1) & (x2,y2) is = (𝑦_2 − 𝑦_1)/(𝑥_2 − 𝑥_1 ) Slope of BC joining (4, –1) & (1, 2) = (2 − (−1))/(1 − 4) = (2 + 1)/( − 3) = 3/(−3) = –1 From (1) Slope of AM = (−1)/(slope of BC) = (−1)/(−1) = 1 Now, finding equation of altitude AM Altitude AM passes through the point A(2, 3) & has slope 1 The equation of line passing through a point (x1, y1) with slope m is (y – y1) = m (x – x1) Putting values for AM: x1 = 2, y1 = 3, & m = 1 (y – 3) = 1(x – 2) x – y + 1 = 0 1 = y – x y – x = 1 Therefore, equation of the altitude AM is y – x = 1. Also, we have to find length of altitude AM Length of AM = Perpendicular distance from point A to line BC To find perpendicular distance, we need to find equation of line BC Finding equation of line BC Slope of line BC = –1 and it passes through the point B(4,–1) The equation of line passing through a point (x1, y1) with slope m is (y – y1) = m (x – x1) Putting values for BC: x1 = 4, y1 = –1 , m = –1 (y – (-1)) = –1(x – 4) (y + 1) = –1 (x – 4) y + 1 = – x + 4 y + x = 4 – 1 y + x = 3 x + y – 3 = 0 Hence, equation of line BC is x + y – 3 = 0 The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by d = |𝐴𝑥_1 + 𝐵𝑦_1 + 𝐶|/√(𝐴^2 + 𝐵^2 ) The above equation is of the form Ax + By + C = 0 Where A = 1 , B = 1 , C = – 3 Also, perpendicular distance from point (2, 3) Hence, x1 = 2, y1 = 3 d = |𝐴𝑥_1 + 𝐵𝑦_1 + 𝐶|/√(𝐴^2 + 𝐵^2 ) Putting values = |1(2) + 1(3) + (−3)|/√((1)2 + (1)2) = |2 + 3 − 3|/√(1 + 1) = |2|/√2 = 2/√2 = 2/√2 × √2/√2 = (2√2)/2 = √2 ∴ Length of altitude AM = √𝟐