Question 25 - CBSE Class 10 Sample Paper for 2026 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Transcript

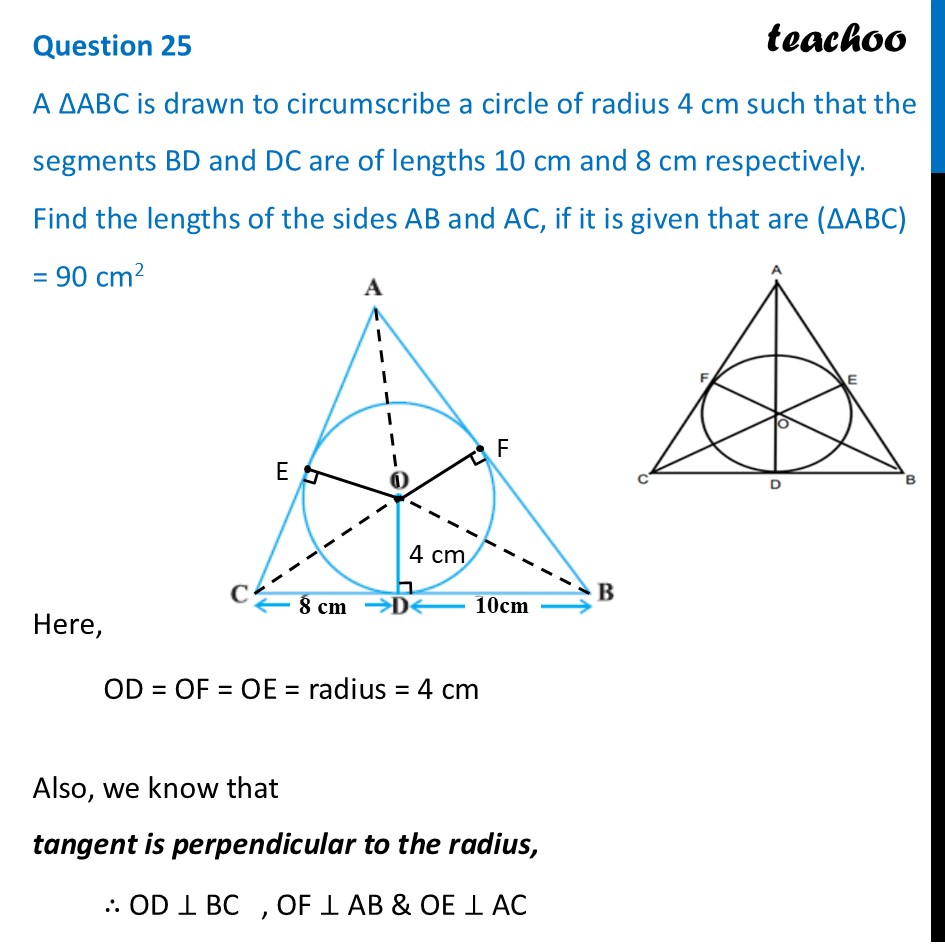
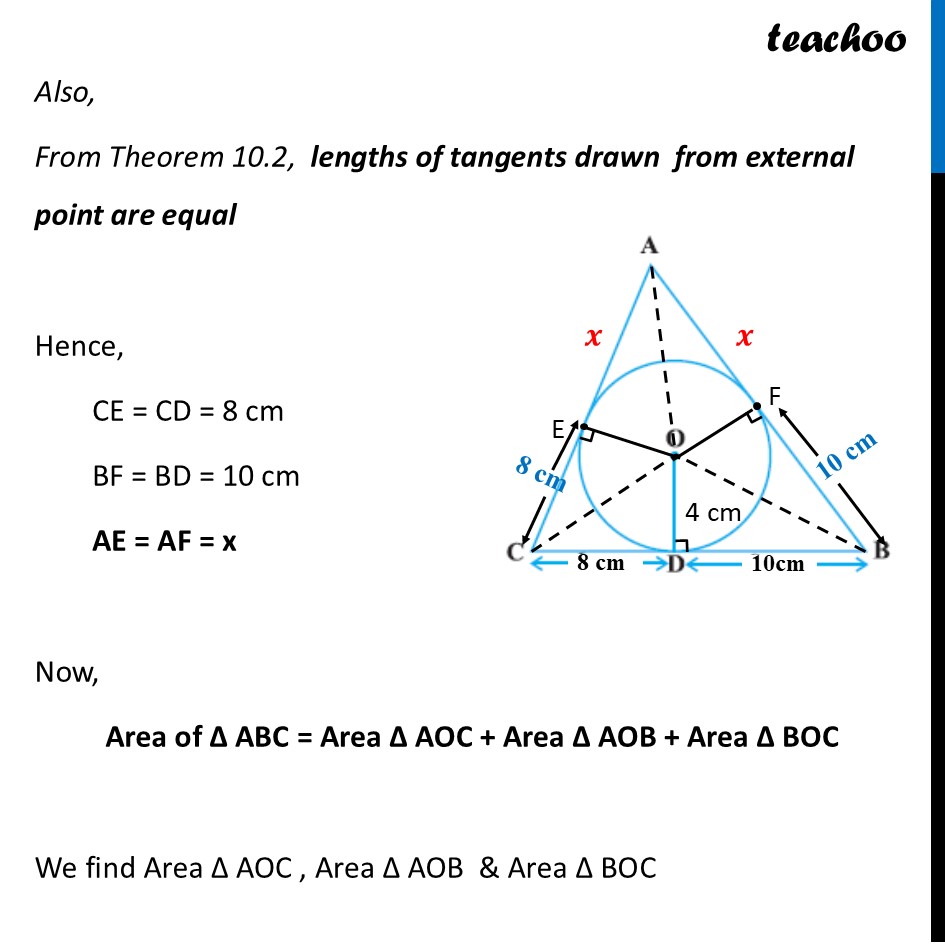
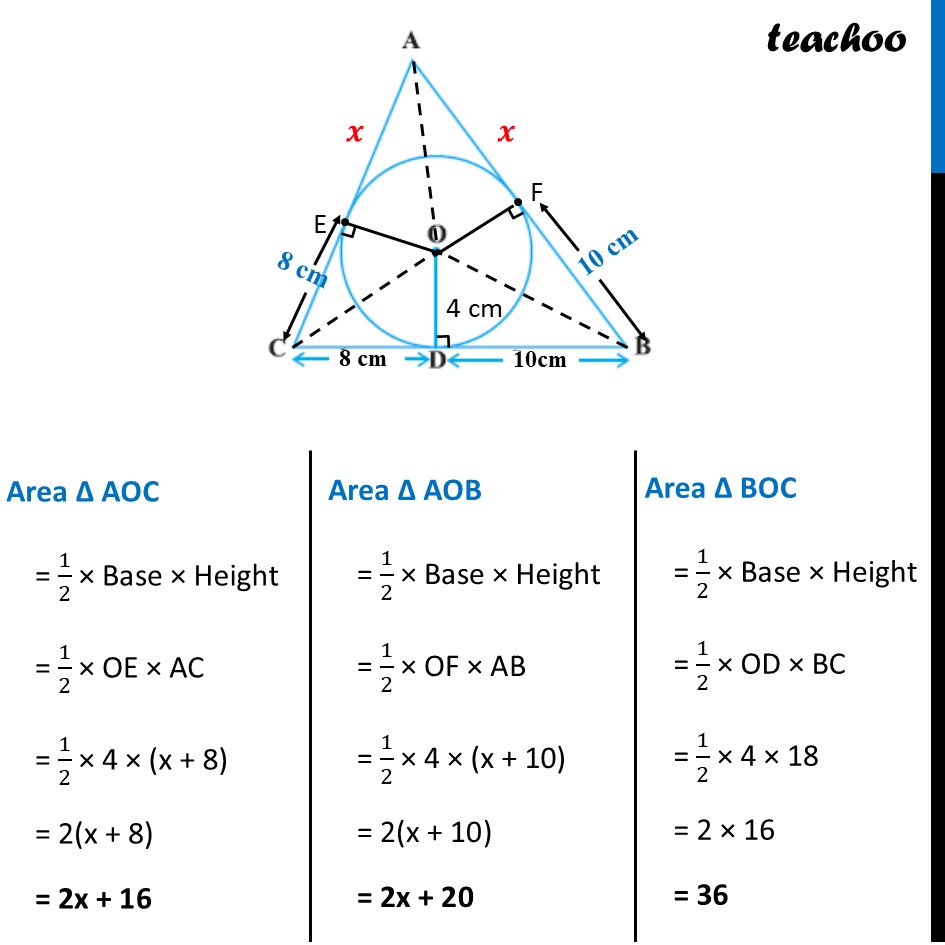
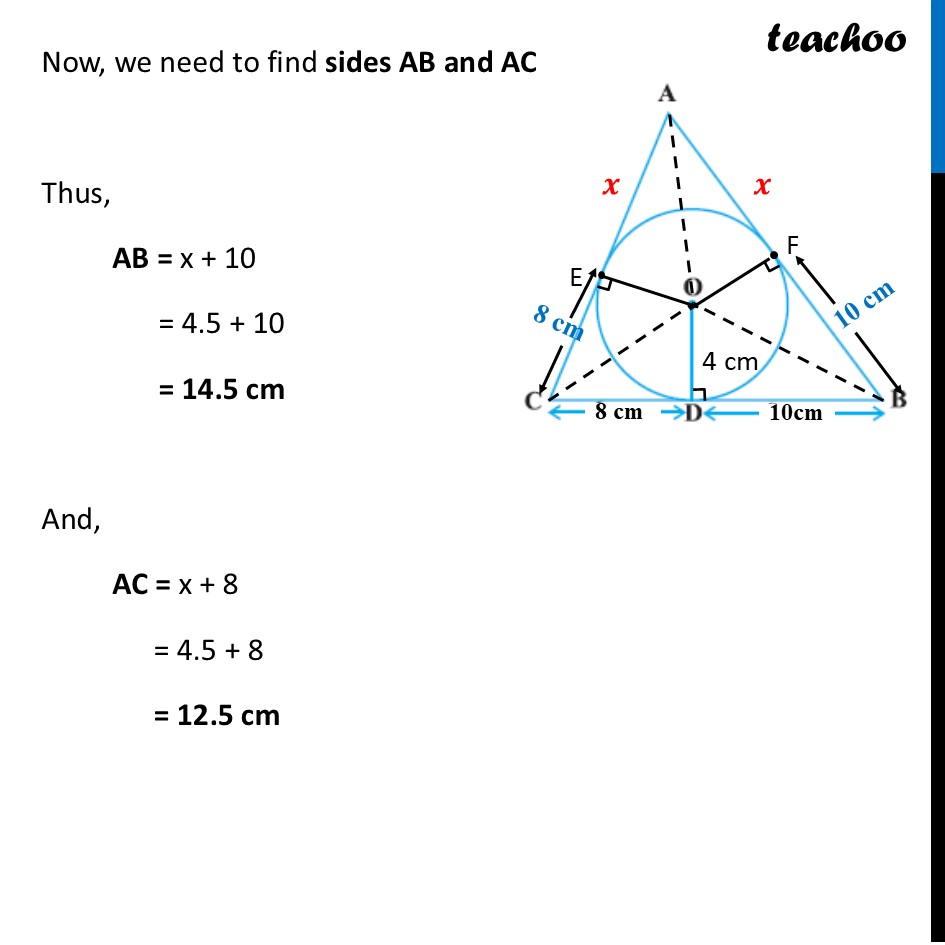
Question 25 A ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 10 cm and 8 cm respectively. Find the lengths of the sides AB and AC, if it is given that are (∆ABC) = 90 cm2Here, OD = OF = OE = radius = 4 cm Also, we know that tangent is perpendicular to the radius, ∴ OD ⊥ BC , OF ⊥ AB & OE ⊥ AC Also, From Theorem 10.2, lengths of tangents drawn from external point are equal Hence, CE = CD = 8 cm BF = BD = 10 cm AE = AF = x Now, Area of Δ ABC = Area Δ AOC + Area Δ AOB + Area Δ BOC We find Area Δ AOC , Area Δ AOB & Area Δ BOC Area Δ AOC = 1/2 × Base × Height = 1/2 × OE × AC = 1/2 × 4 × (x + 8) = 2(x + 8) = 2x + 16 Area Δ AOB = 1/2 × Base × Height = 1/2 × OF × AB = 1/2 × 4 × (x + 10) = 2(x + 10) = 2x + 20 Area Δ BOC = 1/2 × Base × Height = 1/2 × OD × BC = 1/2 × 4 × 18 = 2 × 16 = 36 Now, Area of Δ ABC = Area Δ AOC + Area Δ AOB + Area Δ BOC Putting values 90 = (2x + 16) + (2x + 20) + 36 90 = 2x + 2x + 16 + 20 + 36 90 = 4x + 72 90 – 72 = 4x 18 = 4x 4x = 18 x = 18/2 x = 9/2 x = 4.5 cm √(48𝑥2+672𝑥) = 4x + 56 Squaring both sides (√(48𝑥2+672𝑥))2 = (4x + 56)2 48x2 + 672x = (4x)2 + 562 + 2 × 4x × 56 48x2 + 672x = 16x2 + 3136 + 448x 48x2 – 16x2 + 672x – 448x – 3136 = 0 32x2 + 224x – 3136 = 0 32(x2 + 7x – 98)= 0 x2 + 7x – 98 = 0 x2 + 14x – 7x – 98 = 0 Now, we need to find sides AB and AC Thus, AB = x + 10 = 4.5 + 10 = 14.5 cm And, AC = x + 8 = 4.5 + 8 = 12.5 cm