Ex 10.2, 12 - Chapter 10 Class 10 Circles

Transcript

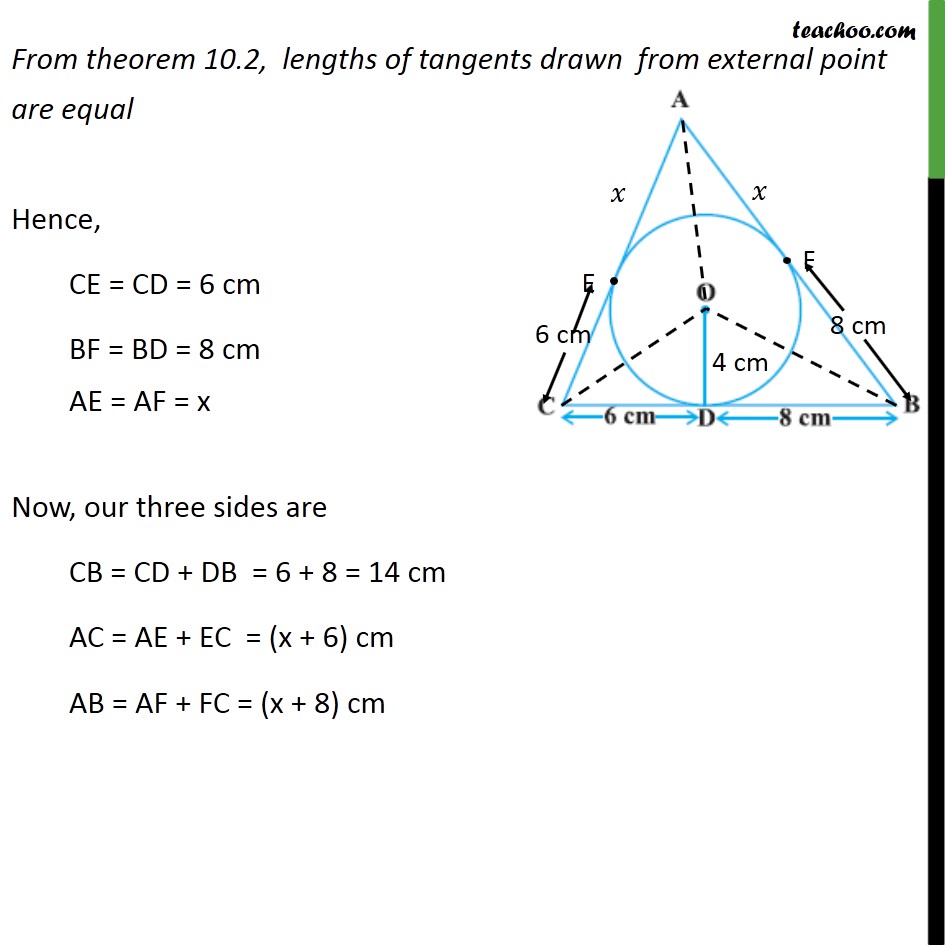
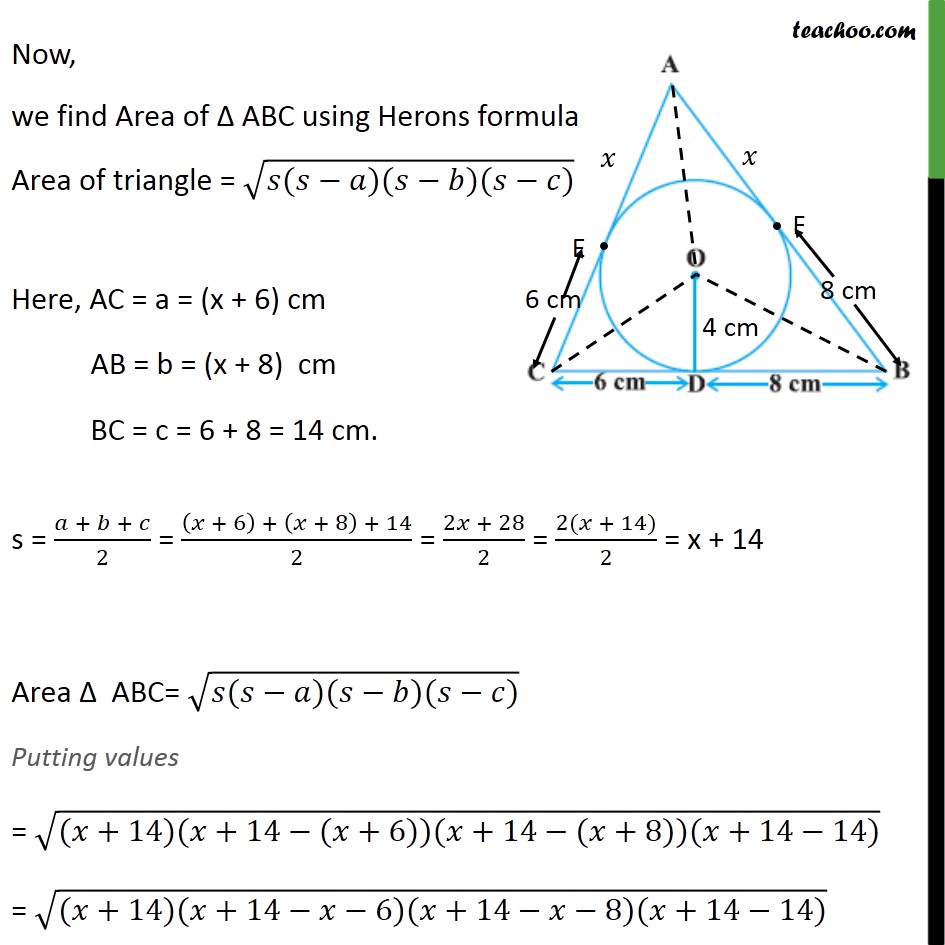
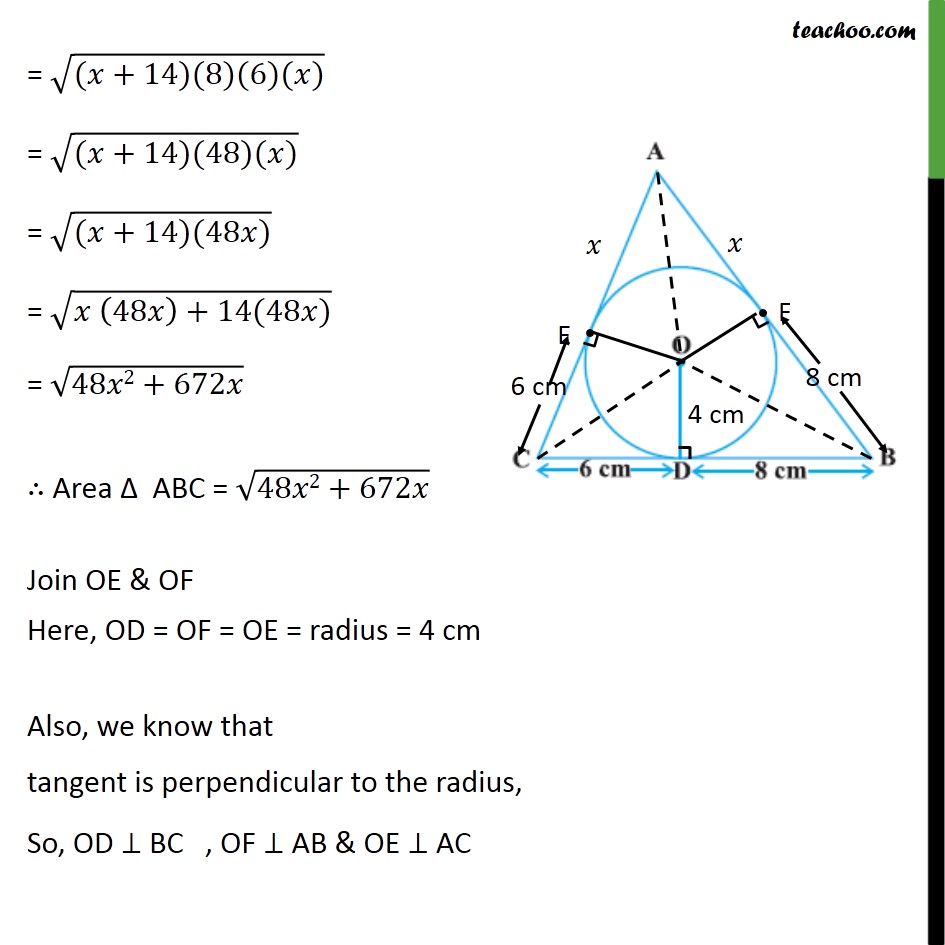
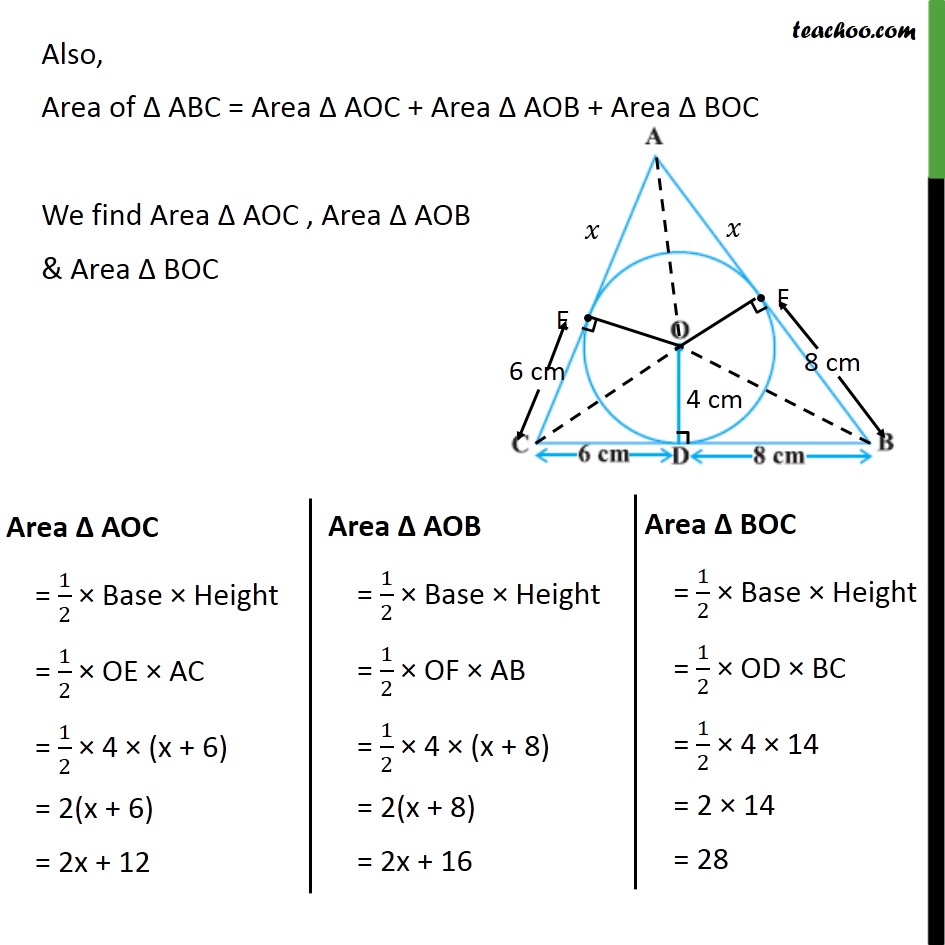
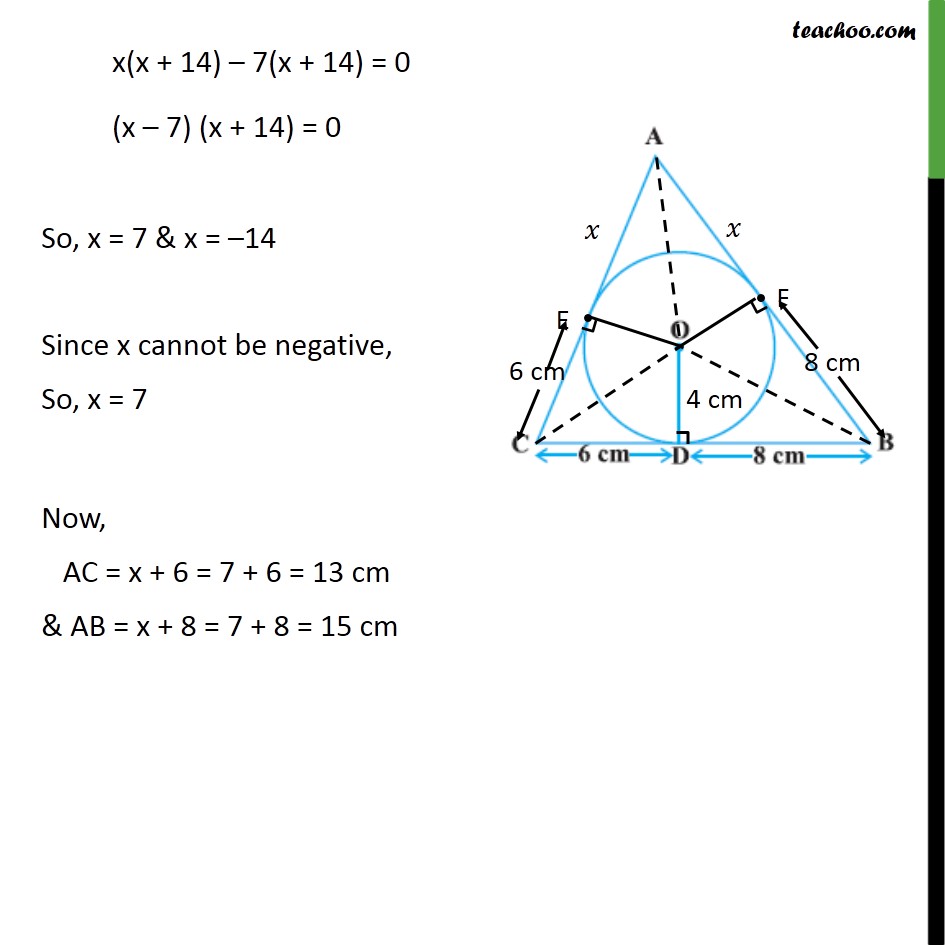
Ex 10.2,12 A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC. Given: A circle with centre O with OD = radius = 4 cm Let ABC circumscribe the circle Also, BD = 8 cm & CD = 6 cm To find: AB & AC Construction: Join OA, OC& OB Let AC, AB intersect circle at E & F respectively Solution: From theorem 10.2, lengths of tangents drawn from external point are equal Hence, CE = CD = 6 cm BF = BD = 8 cm AE = AF = x Now, our three sides are CD = CD + DB = 6 + 8 = 14 cm AC = AE + EC = (x + 6) cm AB = AF + FC = (x + 8) cm Now, we find Area of ABC using Herons formula Area of triangle = ( ( )( )( )) Here, AC = a = (x + 6) cm AB = b = (x + 8) cm BC = c = 6 + 8 = 14 cm. s = ( + + )/2 = (( + 6) + ( + 8) + 14)/2 = (2 + 28)/2 = (2( + 14))/2 = x + 14 Area ABC= ( ( )( )( )) Putting values = (( +14)( +14 ( +6))( +14 ( +8))( +14 14)) = (( +14)( +14 6)( +14 8)( +14 14)) = (( +14)(8)(6)( )) = (( +14)(48)( )) = (( +14)(48 )) = ( (48 )+14(48 )) = (48 2+672 ) Area ABC = (48 2+672 ) Join OE & OF Here, OD = OF = OE = radius = 4 cm Also, we know that tangent is perpendicular to the radius, So, OD BC , OF AB & OE AC Also, Area of ABC = Area AOC + Area AOB + Area BOC We find Area AOC , Area AOB & Area BOC Now, Area of ABC = Area AOC + Area AOB + Area BOC Putting values (48 2+672 ) = (2x + 12) + (2x + 16) + 28 (48 2+672 ) = 4x + 56 Squaring both sides ( (48 2+672 ))2 = (4x + 56)2 48x2 + 672x = (4x)2 + 562 + 2 4x 56 48x2 + 672x = 16x2 + 3136 + 448x 48x2 16x2 + 672x 448x 3136 = 0 32x2 + 224x 3136 = 0 32(x2 + 7x 98)= 0 x2 + 7x 98 = 0 x2 + 14x 7x 98 = 0 x(x + 14) 7(x + 14) = 0 (x 7) (x + 14) = 0 So, x = 7 & x = 14 Since x cannot be negative, So, x = 7 Now, AC = x + 6 = 7 + 6 = 13 cm & AB = x + 8 = 7 + 8 = 15 cm