Ex 10.2, 7 - Chapter 10 Class 10 Circles

Transcript

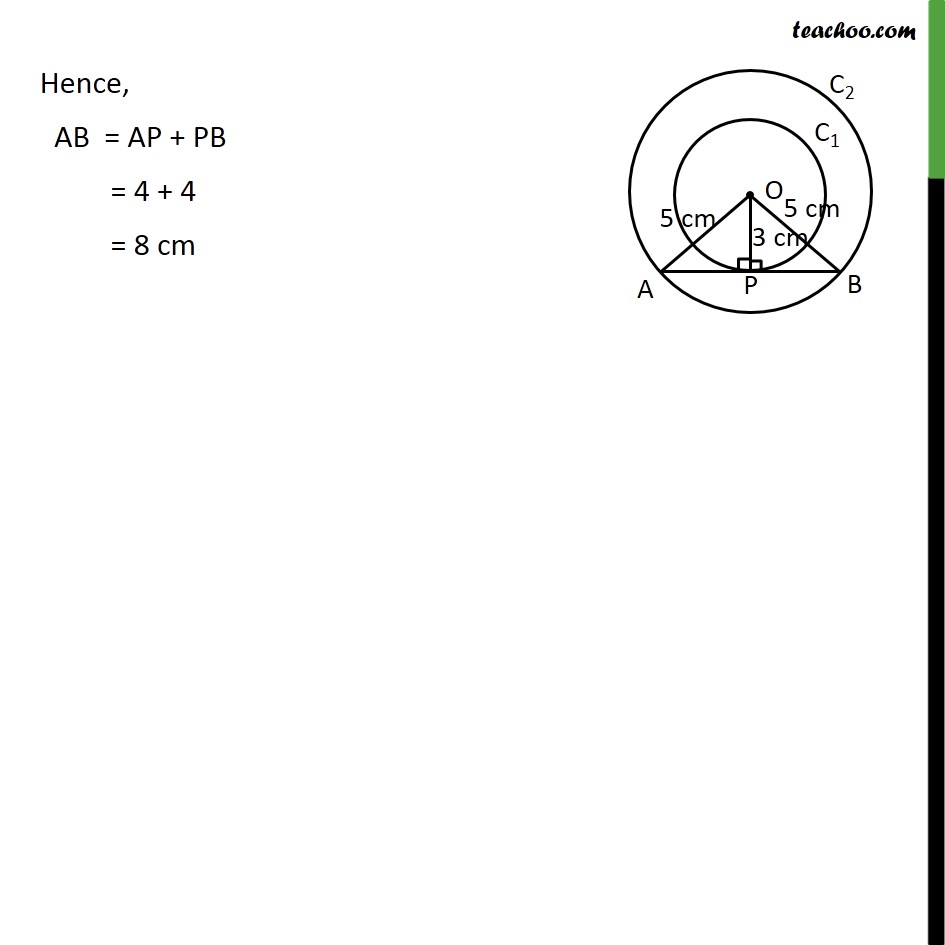
Ex 10.2,7 Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle. Given: Let two concentric circles be C1 & C2 with center O AB be chord of the larger circle C2 which touches the smaller circle C1 at point P To find: Length of AB Solution: Connecting OP, OA and OB OP = Radius of smaller circle = 3 cm OA = OB = Radius of larger circle = 5 cm Since AB is tangent to circle C1 OP ⊥ AB ∴ ∠ OPA = ∠ OPB = 90° Using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 Hence, AB = AP + PB = 4 + 4 = 8 cm