
Last updated at Dec. 13, 2024 by Teachoo


Transcript
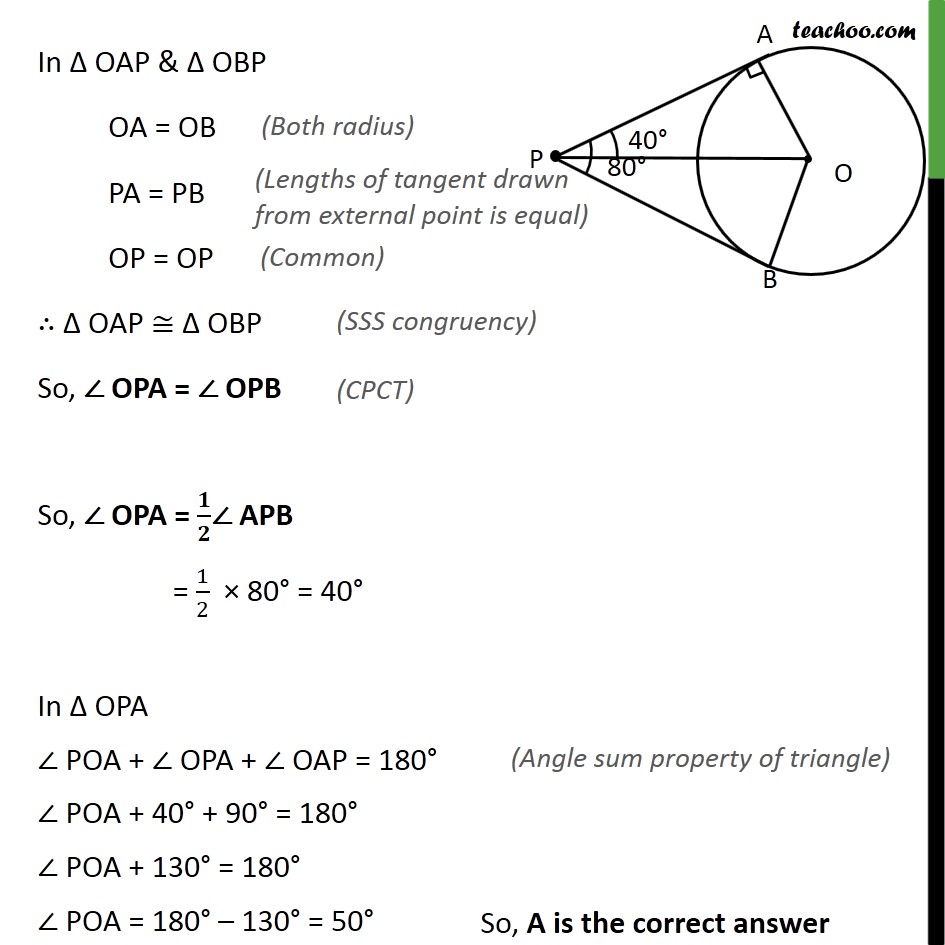
Ex 10.2,3 Choose the correct option and give justification. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80 , then POA is equal to (A) 50 (B) 60 (C) 70 (D) 80 Given: PA and PB are tangents to circle & APB = 80 To find: POA Construction: Join OA,OB & OP Proof: Since PA is tangent, OA PA OAP = 90 In OAP & OBP OA = OB PA = PB OP = OP OAP OBP So, OPA = OPB So, OPA = / APB = 1/2 80 = 40 In OPA POA + OPA + OAP = 180 POA + 40 + 90 = 180 POA + 130 = 180 POA = 180 130 = 50 So, A is the correct answer