Theorem 10.1
Last updated at Nov. 27, 2017 by Teachoo
Transcript
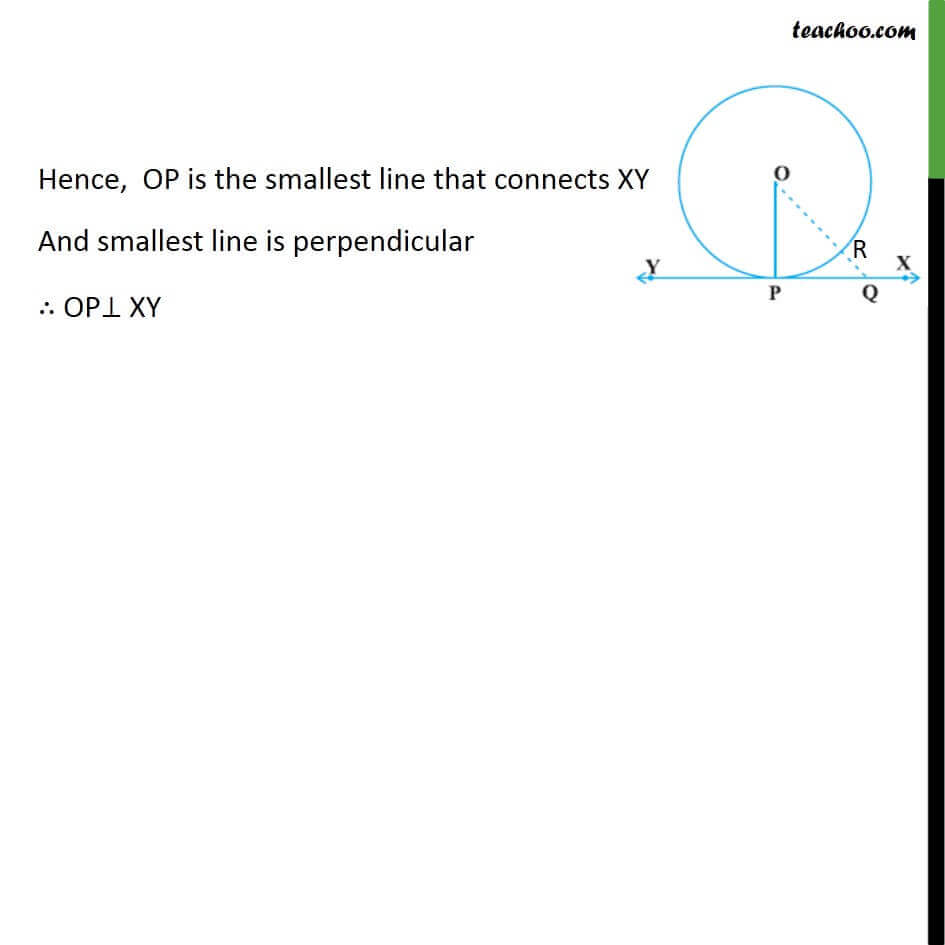
Theorem 10.1 The tangent at any point of a circle is perpendicular to the radius through the point of contact. Given: A circle with center O. With tangent XY at point of contact P. To prove: OP ⊥ XY Proof: Let Q be point on XY Connect OQ Suppose it touches the circle at R Hence, OQ >𝑂𝑅 OQ >𝑂𝑃 Same will be the case with all other points on circle Hence, OP is the smallest line that connects XY Hence, OP is the smallest line that connects XY And smallest line is perpendicular ∴ OP⊥ XY
About the Author
Davneet Singh
Davneet Singh is a graduate from Indian Institute of Technology, Kanpur. He has been teaching from the past 8 years. He provides courses for Maths and Science at Teachoo. You can check his NCERT Solutions from Class 6 to 12.
-
Please reply with a detailed solution.
Please reply with a detailed solution.
prove that lone segment joining the points of contact of two parallel tangents passes through the centre
Or =oq why
Why you have contruct a line in therom 10.1
The saved posts are not opening,,,,,What can I do????
hello sir,
please give detailed explanation to "alternate segment theorem" becoz it is not in the text book, and expl.....n given to this theorem by various sources are not accurate and more over they are not trusted,please take immediate action for this. hope u will do favour for students.
