Ex 10.2, 11 - Chapter 10 Class 10 Circles

Last updated at April 16, 2024 by

Ex 10.2, 11 - Prove that parallelogram circumscribing a circle - Theorem 10.2: Equal tangents from external point (proof type)

Ex 10.2, 11 - Chapter 10 Class 10 Circles - Part 2
Ex 10.2, 11 - Chapter 10 Class 10 Circles - Part 3

Go Ad-free

Transcript

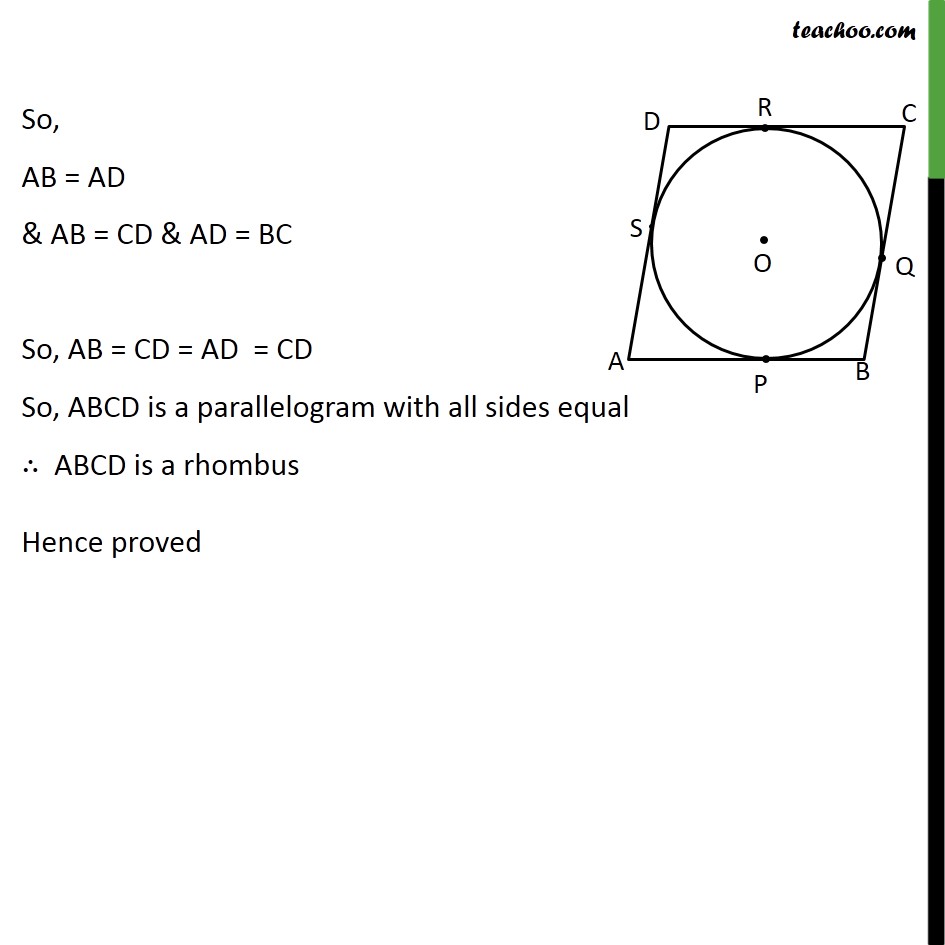
Ex 10.2,11 Prove that the parallelogram circumscribing a circle is a rhombus. Given: A circle with centre O. A parallelogram ABCD touching the circle at points P,Q,R and S To prove: ABCD is a rhombus Proof: A rhombus is a parallelogram with all sides equal, So, we have to prove all sides equal In parallelogram ABCD, AB = CD & AD = BC From theorem 10.2, lengths of tangents drawn from external point are equal Hence, AP = AS BP = BQ CR = CQ DR = DS Adding (2) + (3) + (4) + (5) AP + BP + CR + DR = AS + BQ + CQ + DS (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ) AB + CD = AD + BC AB + AB = AD + AD 2AB = 2AD AB = AD So, AB = AD & AB = CD & AD = BC So, AB = CD = AD = CD So, ABCD is a parallelogram with all sides equal ABCD is a rhombus Hence proved

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo