[SQP] If AP and DQ are medians of triangles ABC and DEF respectively

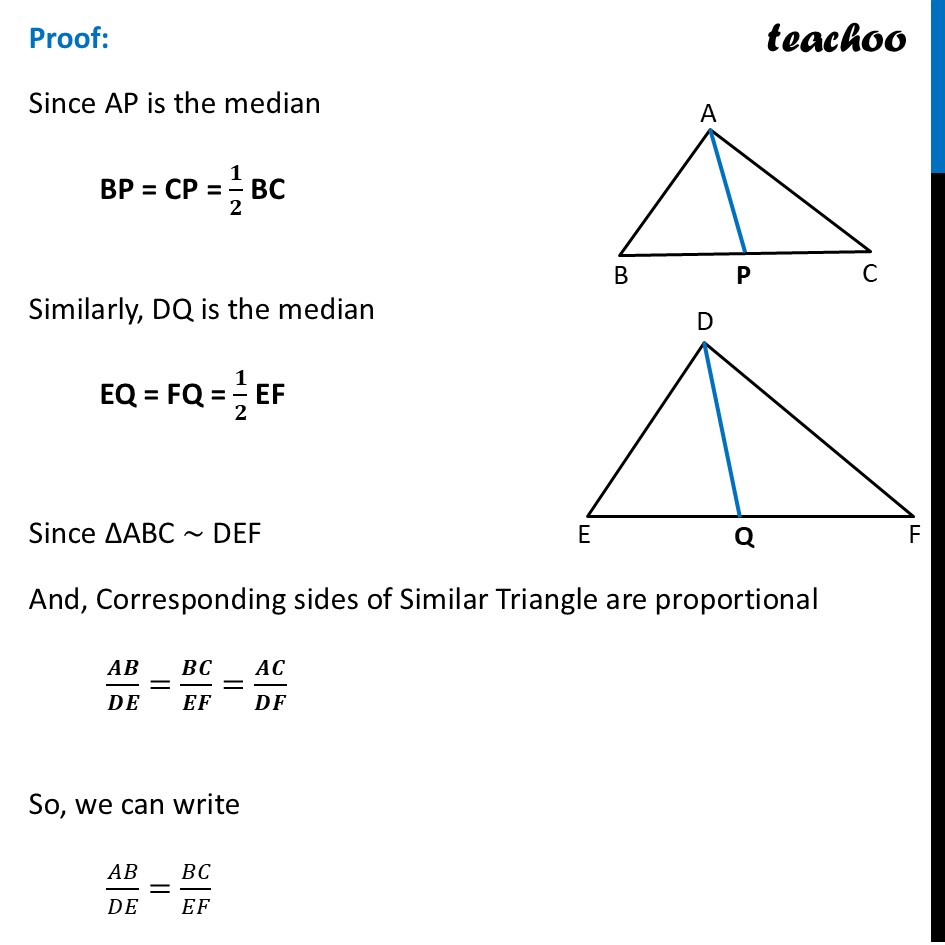
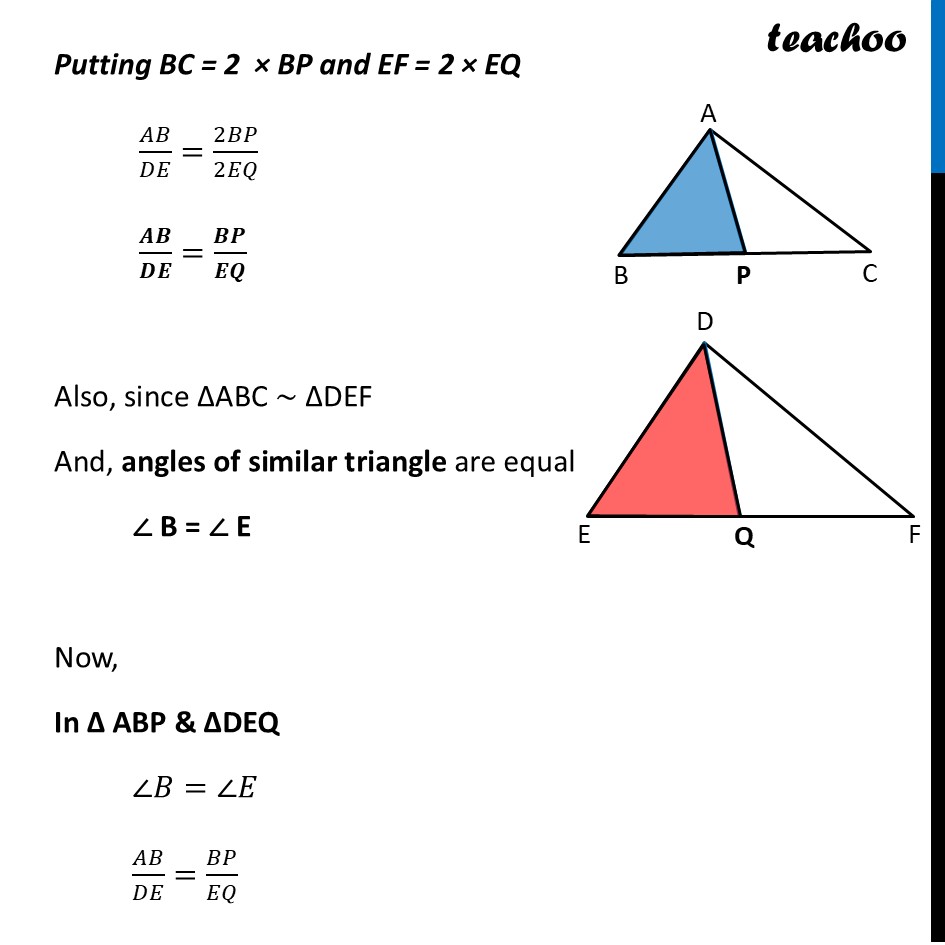
Question 23 If AP and DQ are medians of triangles ABC and DEF respectively, where △ABC∼△DEF, then prove that 𝐴𝐵/𝐷𝐸=𝐴𝑃/𝐷𝑄 Given: ΔABC and ΔDEF AP is the median of Δ ABC & DQ is the median of Δ DEF & ΔABC ∼ Δ DEF To Prove:- 𝐴𝐵/𝐷𝐸=𝐴𝑃/𝐷𝑄 Proof: Since AP is the median BP = CP = 𝟏/𝟐 BC Similarly, DQ is the median EQ = FQ = 𝟏/𝟐 EF Since ΔABC ∼ DEF And, Corresponding sides of Similar Triangle are proportional 𝑨𝑩/𝑫𝑬=𝑩𝑪/𝑬𝑭=𝑨𝑪/𝑷𝑹 So, we can write 𝐴𝐵/𝐷𝐸=𝐵𝐶/𝐸𝐹 Putting BC = 2 × BP and EF = 2 × EQ 𝐴𝐵/𝐷𝐸=2𝐵𝑃/2𝐸𝑄 𝑨𝑩/𝑫𝑬=𝑩𝑷/𝑬𝑸 Also, since ΔABC ∼ ΔDEF And, angles of similar triangle are equal ∠ B = ∠ E Now, In Δ ABP & ΔDEQ ∠𝐵=∠𝑄 𝐴𝐵/𝐷𝐸=𝐵𝑃/𝐸𝑄 Hence by SAS similarly ΔABP ∼ ΔDEQ Since corresponding sides of similar triangles are proportional ∴ 𝑨𝑩/𝑷𝑸=𝑨𝑫/𝑷𝑴 Hence proved

Question 23 - CBSE Class 10 Sample Paper for 2026 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Davneet Singh

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular