CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard
You are here
CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard
Last updated at February 12, 2025 by Teachoo
This question is similar to Chapter 6 Class 10 Triangles - Ratio of Area of Similar Triangles
Please check the Question here
Transcript
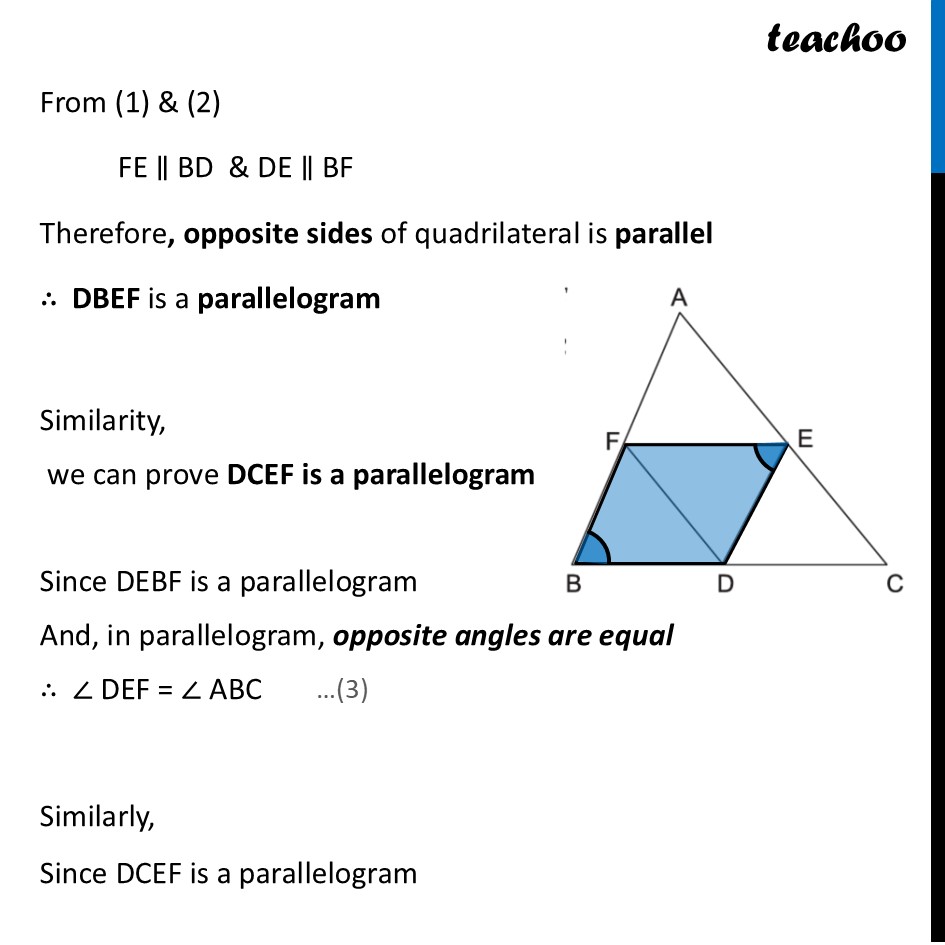
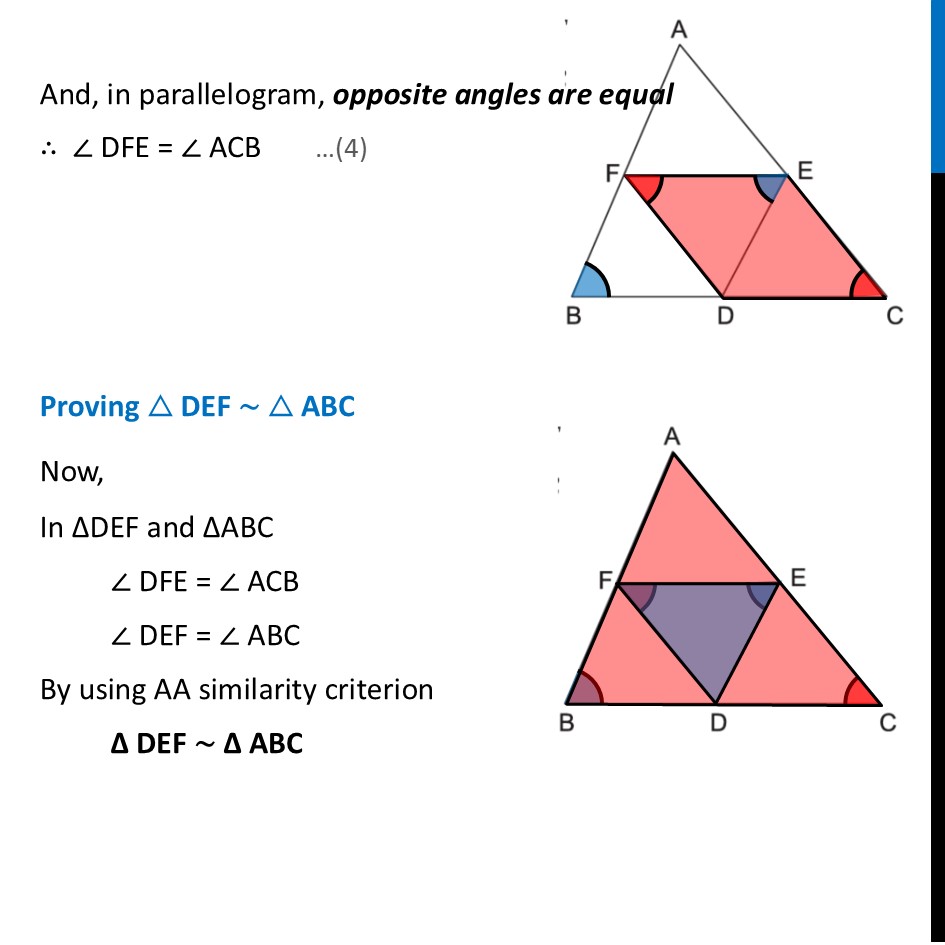
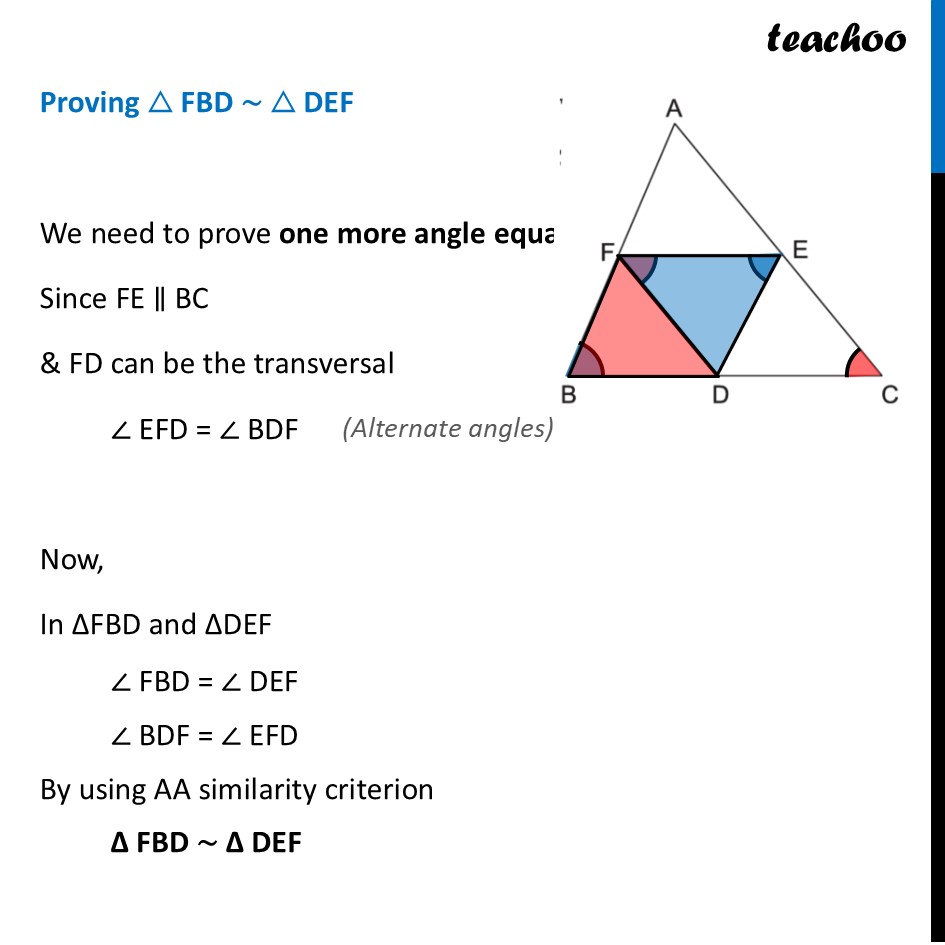
Question 26 (A) In 𝛥ABC, D, E and F are midpoints of BC,CA and AB respectively. Prove that △ 𝐹𝐵𝐷 ∼ △ DEF and △ DEF ∼ △ ABC We know that line joining mid-points of two sides of a triangle is parallel to the 3rd side In ΔABC , F and E are mid-points of AB and AC resp., ∴ FE ∥ BC So, FE ∥ BD also Similarly, D and E are mid-points of BC and AC resp. ∴ DE ∥ AB So, DE ∥ BF also From (1) & (2) FE ∥ BD & DE ∥ BF Therefore, opposite sides of quadrilateral is parallel ∴ DBEF is a parallelogram Similarity, we can prove DCEF is a parallelogram Since DEBF is a parallelogram And, in parallelogram, opposite angles are equal ∴ ∠ DEF = ∠ ABC Similarly, Since DCEF is a parallelogram And, in parallelogram, opposite angles are equal ∴ ∠ DFE = ∠ ACB Proving △ DEF ∼ △ ABC Now, In ΔDEF and ΔABC ∠ DFE = ∠ ACB ∠ DEF = ∠ ABC By using AA similarity criterion Δ DEF ∼ Δ ABC Proving △ FBD ∼ △ DEF We need to prove one more angle equal Since FE ∥ BC & FD can be the transversal ∠ EFD = ∠ BDF Now, In ΔFBD and ΔDEF ∠ FBD = ∠ DEF ∠ BDF = ∠ EFD By using AA similarity criterion Δ FBD ∼ Δ DEF
