Question 5 - Ratio of Area of Similar Triangles - Chapter 6 Class 10 Triangles

Transcript

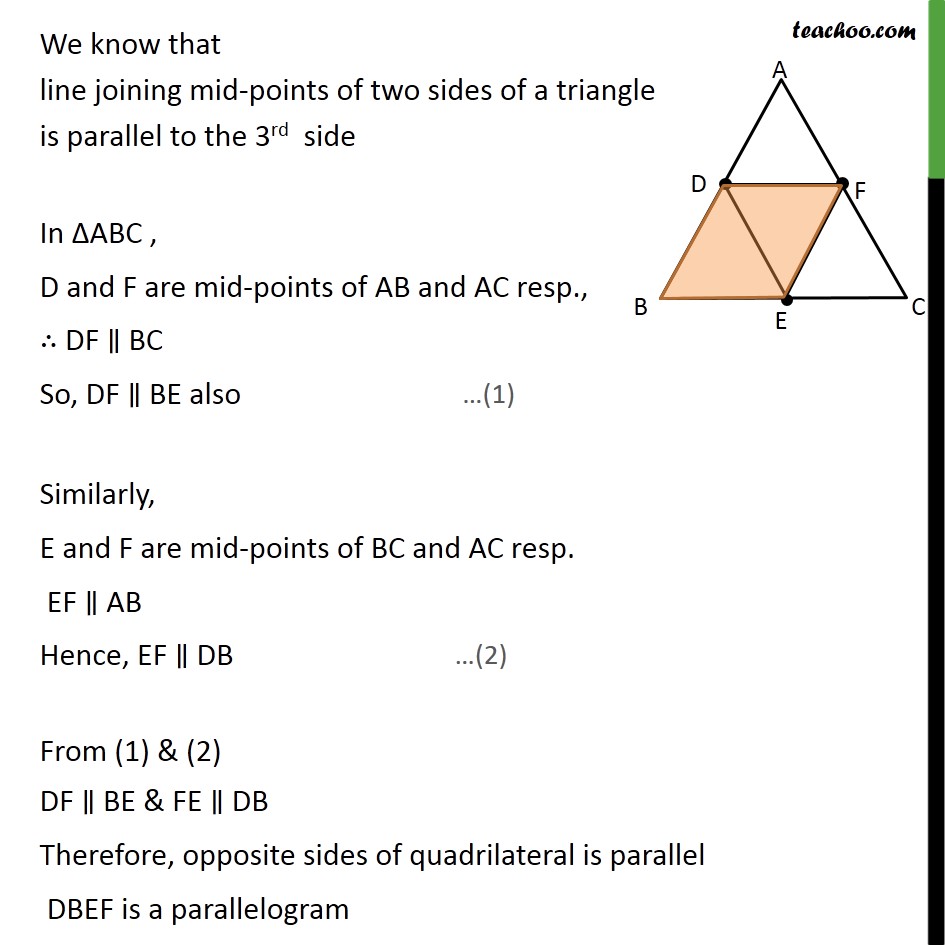
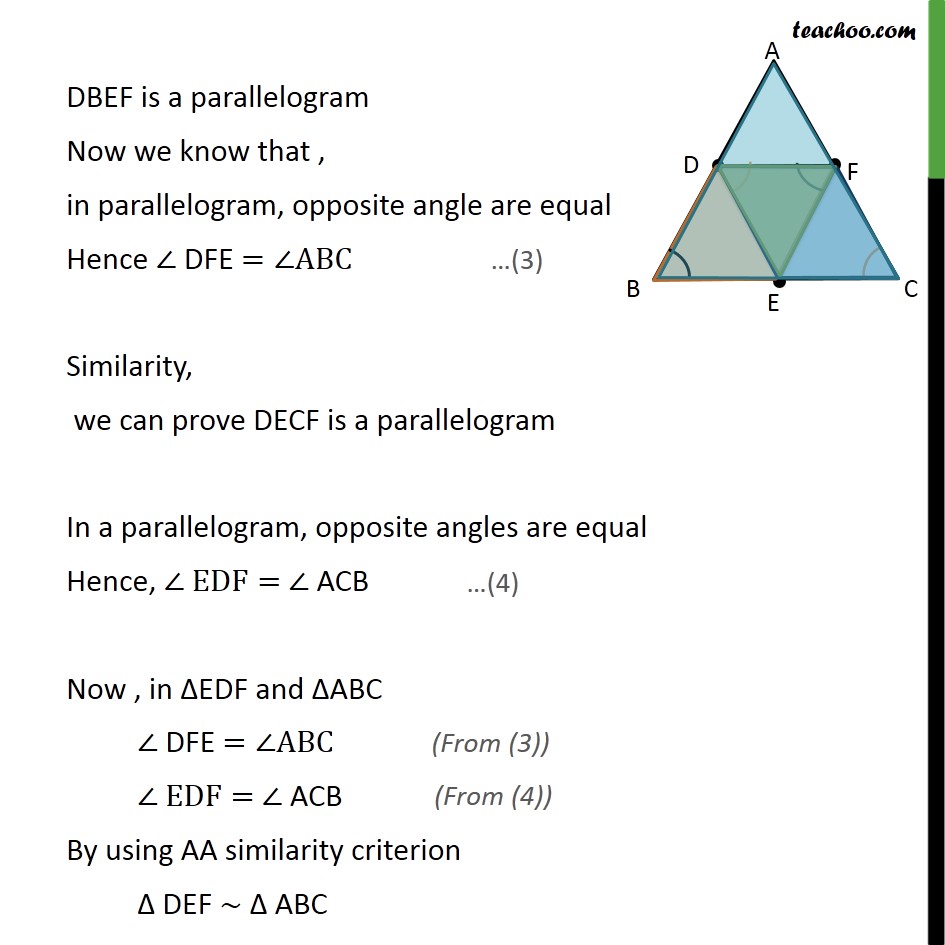
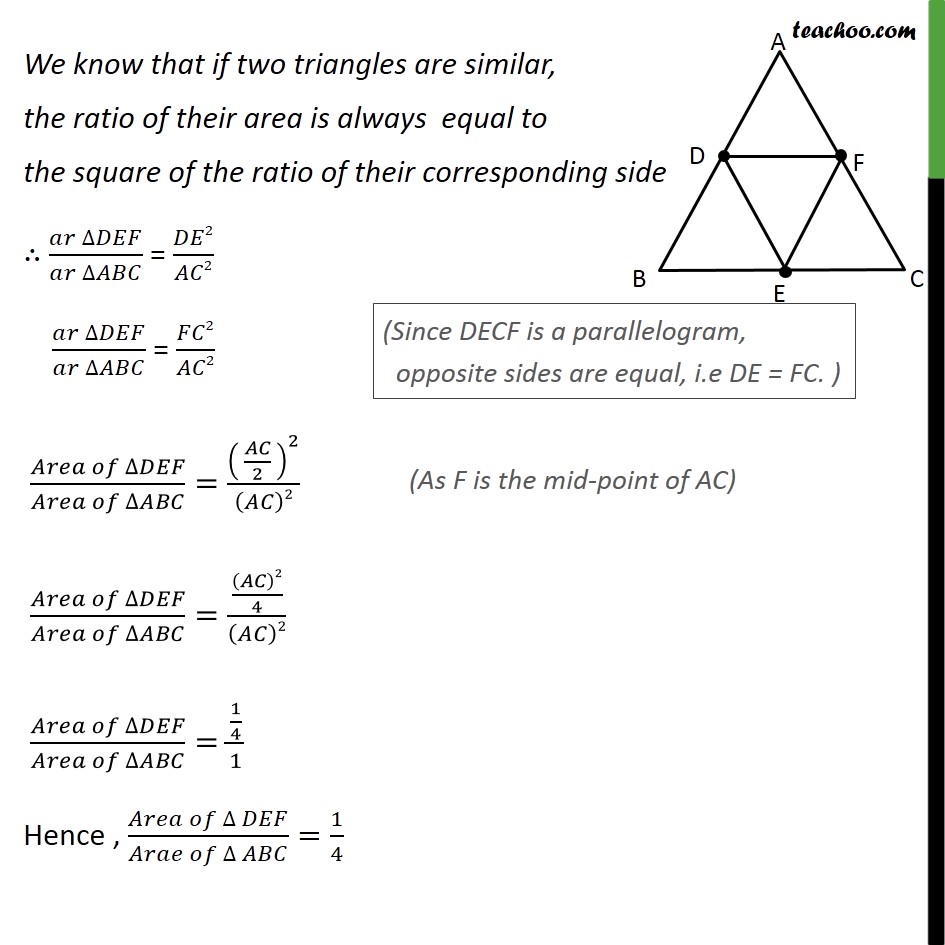
Question 5 D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC. Given: Δ ABC & D,E,F mid-points of AB,BC & CA respectively To find: (𝑎𝑟 ∆𝐷𝐸𝐹)/(𝑎𝑟 ∆𝐴𝐵𝐶) Note: Since we need to find ratio of area of ΔDEF and ΔABC. We first need to prove these triangles are similar Solution: We know that line joining mid-points of two sides of a triangle is parallel to the 3rd side In ΔABC , D and F are mid-points of AB and AC resp., ∴ DF ∥ BC So, DF ∥ BE also Similarly, E and F are mid-points of BC and AC resp. EF ∥ AB Hence, EF ∥ DB From (1) & (2) DF ∥ BE & FE ∥ DB Therefore, opposite sides of quadrilateral is parallel DBEF is a parallelogram DBEF is a parallelogram Now we know that , in parallelogram, opposite angle are equal Hence ∠ DFE =∠ABC Similarity, we can prove DECF is a parallelogram In a parallelogram, opposite angles are equal Hence, ∠ EDF= ∠ ACB Now , in ΔEDF and ΔABC ∠ DFE =∠ABC ∠ EDF= ∠ ACB By using AA similarity criterion Δ DEF ∼ Δ ABC We know that if two triangles are similar, the ratio of their area is always equal to the square of the ratio of their corresponding side ∴ (𝑎𝑟 ∆𝐷𝐸𝐹)/(𝑎𝑟 ∆𝐴𝐵𝐶) = 𝐷𝐸2/𝐴𝐶2 (𝑎𝑟 ∆𝐷𝐸𝐹)/(𝑎𝑟 ∆𝐴𝐵𝐶) = 𝐹𝐶2/𝐴𝐶2 (𝐴𝑟𝑒𝑎 𝑜𝑓 ∆𝐷𝐸𝐹)/(𝐴𝑟𝑒𝑎 𝑜𝑓 ∆𝐴𝐵𝐶)=( 𝐴𝐶/2 )^2/(𝐴𝐶)2 (𝐴𝑟𝑒𝑎 𝑜𝑓 ∆𝐷𝐸𝐹)/(𝐴𝑟𝑒𝑎 𝑜𝑓 ∆𝐴𝐵𝐶)=((𝐴𝐶)2/4)/(𝐴𝐶)2 (𝐴𝑟𝑒𝑎 𝑜𝑓 ∆𝐷𝐸𝐹)/(𝐴𝑟𝑒𝑎 𝑜𝑓 ∆𝐴𝐵𝐶)=(1/4)/1 Hence , (𝐴𝑟𝑒𝑎 𝑜𝑓 ∆ 𝐷𝐸𝐹)/(𝐴𝑟𝑎𝑒 𝑜𝑓 ∆ 𝐴𝐵𝐶)=1/4