Question 4 - Ratio of Area of Similar Triangles - Chapter 6 Class 10 Triangles

Transcript

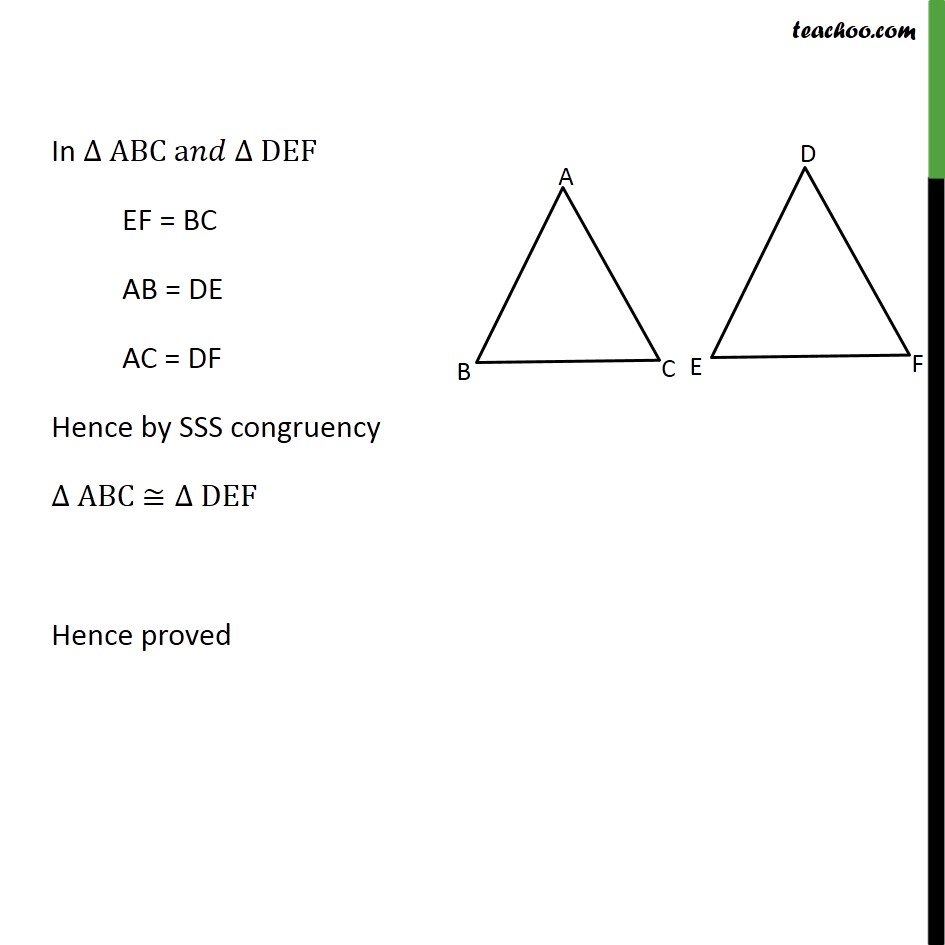
Question 4 If the areas of two similar triangles are equal, prove that they are congruent. Given: Let triangles be Δ ABC & Δ DEF Both triangles are similar, i.e.,∆ ABC ~∆ DEF and Areas are equal, i.e., ar Δ ABC = ar Δ DEF To prove: Both triangles are congruent, i.e.∆ ABC ≅∆ DEF Proof: Given ∆ ABC ~∆ DEF We know that if two triangle are similar , Ratio of areas is equal to square of ratio of its corresponding sides (𝑎𝑟 ∆ 𝐴𝐵𝐶)/(𝑎𝑟 ∆ 𝐷𝐸𝐹)=(𝐵𝐶/𝐸𝐹 )^2=( 𝐴𝐵/𝐷𝐸 )^2=( 𝐴𝐶/𝐷𝐹 )^2 (𝑎𝑟 ∆ 𝐷𝐸𝐹)/(𝑎𝑟 ∆ 𝐷𝐸𝐹)=(𝐵𝐶/𝐸𝐹 )^2=( 𝐴𝐵/𝐷𝐸 )^2=( 𝐴𝐶/𝐷𝐹 )^2 1 =(𝐵𝐶/𝐸𝐹 )^2=( 𝐴𝐵/𝐷𝐸 )^2=( 𝐴𝐶/𝐷𝐹 )^2 Taking In ∆ ABC a𝑛𝑑 ∆ DEF EF = BC AB = DE AC = DF Hence by SSS congruency ∆ ABC ≅∆ DEF Hence proved