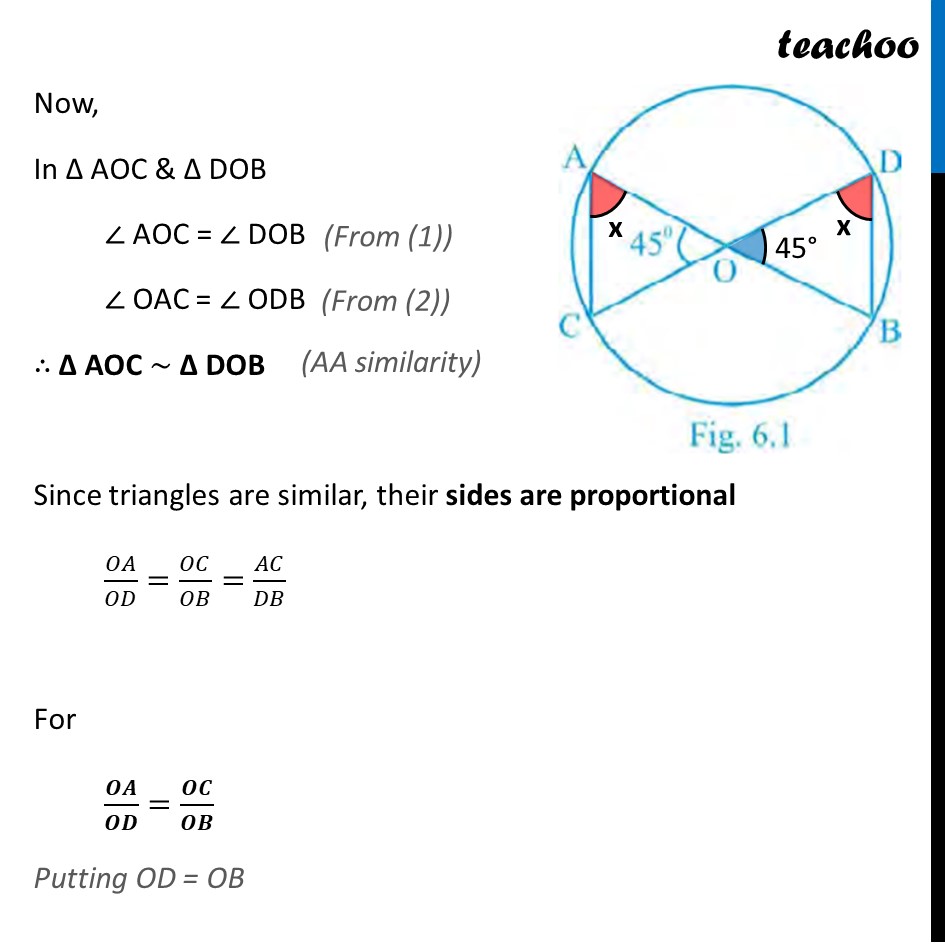
If in Fig 6.1, O is the point of intersection of two chords AB
and CD such that OB = OD, then triangles OAC and ODB are
(A)equilateral but not similar
(B) isosceles but not similar
(C) equilateral and similar
(D) isosceles and similar

Last updated at Dec. 16, 2024 by Teachoo



Transcript
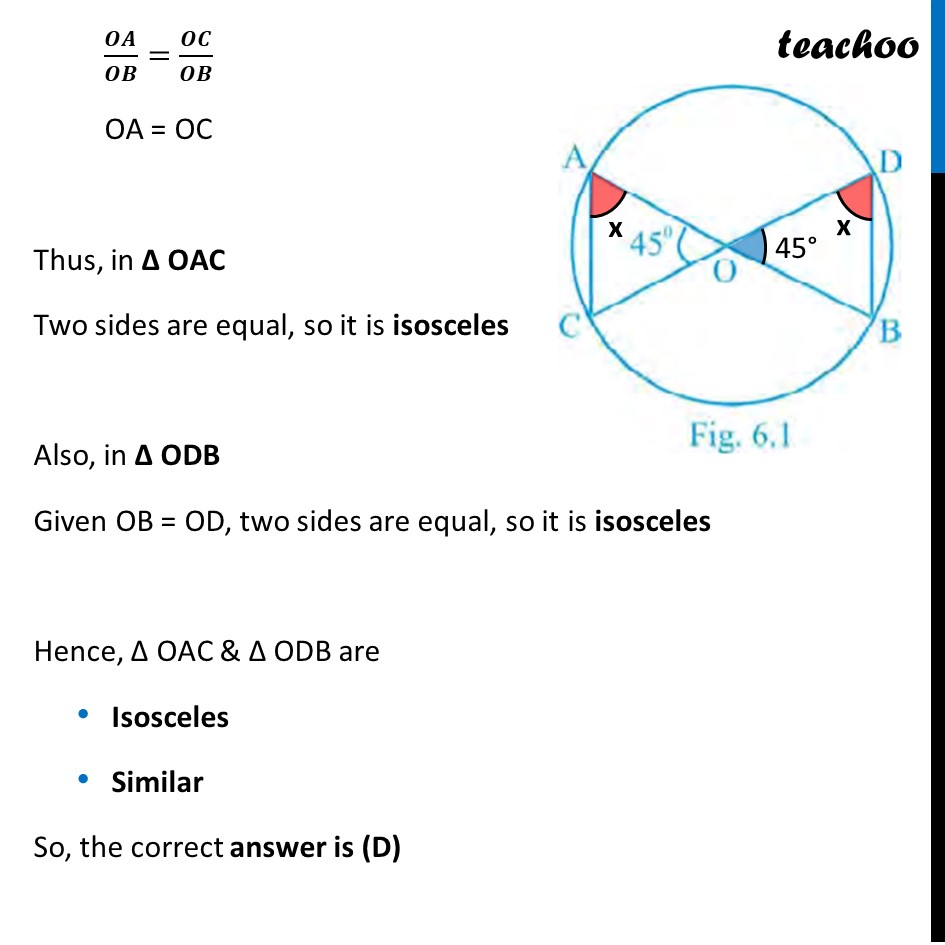
Question 1 If in Fig 6.1, O is the point of intersection of two chords AB and CD such that OB = OD, then triangles OAC and ODB are equilateral but not similar (B) isosceles but not similar (C) equilateral and similar (D) isosceles and similar Here, ∠ AOC = ∠ DOB Also, ∠ ODB = OAC (Vertically opposite angles) (Angle in the same segment are equal) Now, In Δ AOC & Δ DOB ∠ AOC = ∠ DOB ∠ OAC = ∠ ODB ∴ Δ AOC ~ Δ DOB Since triangles are similar, their sides are proportional 𝑂𝐴/𝑂𝐷=𝑂𝐶/𝑂𝐵=𝐴𝐶/𝐷𝐵 For 𝑶𝑨/𝑶𝑫=𝑶𝑪/𝑶𝑩 Putting OD = OB (From (1)) (From (2)) (AA similarity) 𝑶𝑨/𝑶𝑩=𝑶𝑪/𝑶𝑩 OA = OC Thus, in Δ OAC Two sides are equal, so it is isosceles Also, in Δ ODB Given OB = OD, two sides are equal, so it is isosceles Hence, Δ OAC & Δ ODB are Isosceles Similar So, the correct answer is (D)