Check sibling questions

Question 14 - NCERT Exemplar - MCQ - Chapter 6 Class 10 Triangles

Last updated at May 29, 2023 by

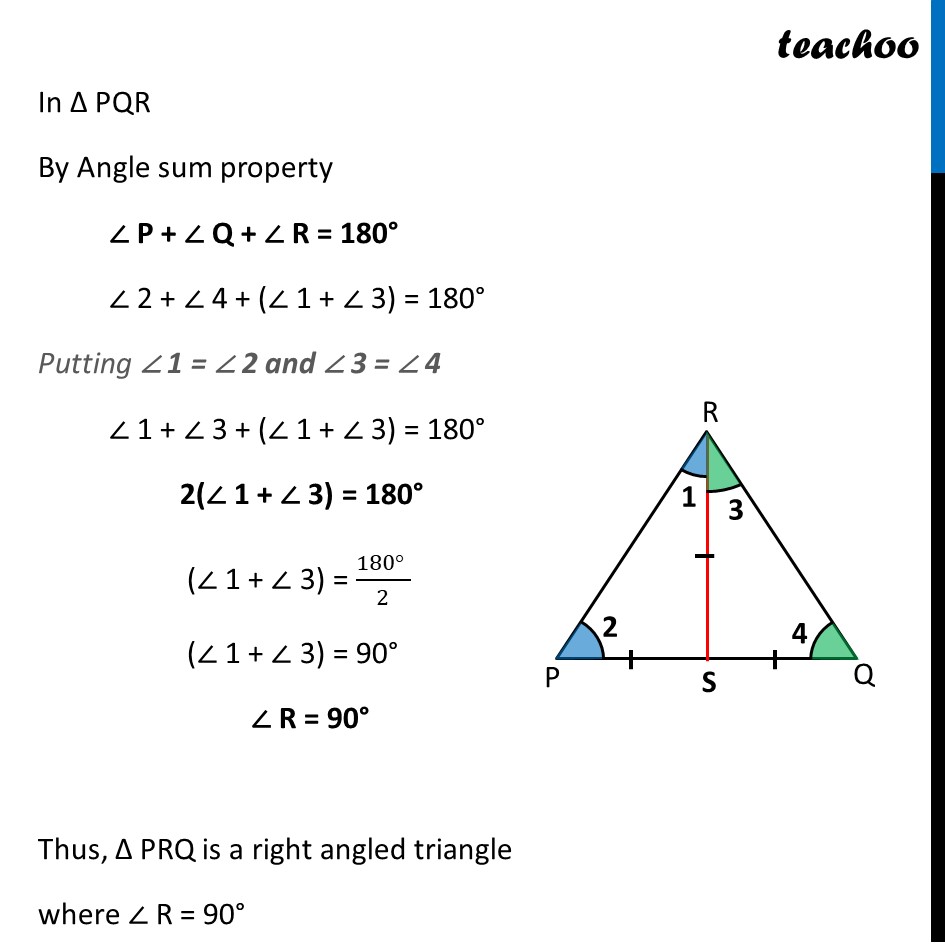
If S is a point on side PQ of a ∆  PQR such that PS = QS = RS, then

(A)PR . QR = RS 2  

(B) QS 2 + RS 2 = QR 2

(C) PR 2 + QR 2 = PQ 2  

(D) PS 2 + RS 2 = PR 2

Slide30.JPG

Slide31.JPG
Slide32.JPG

 

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

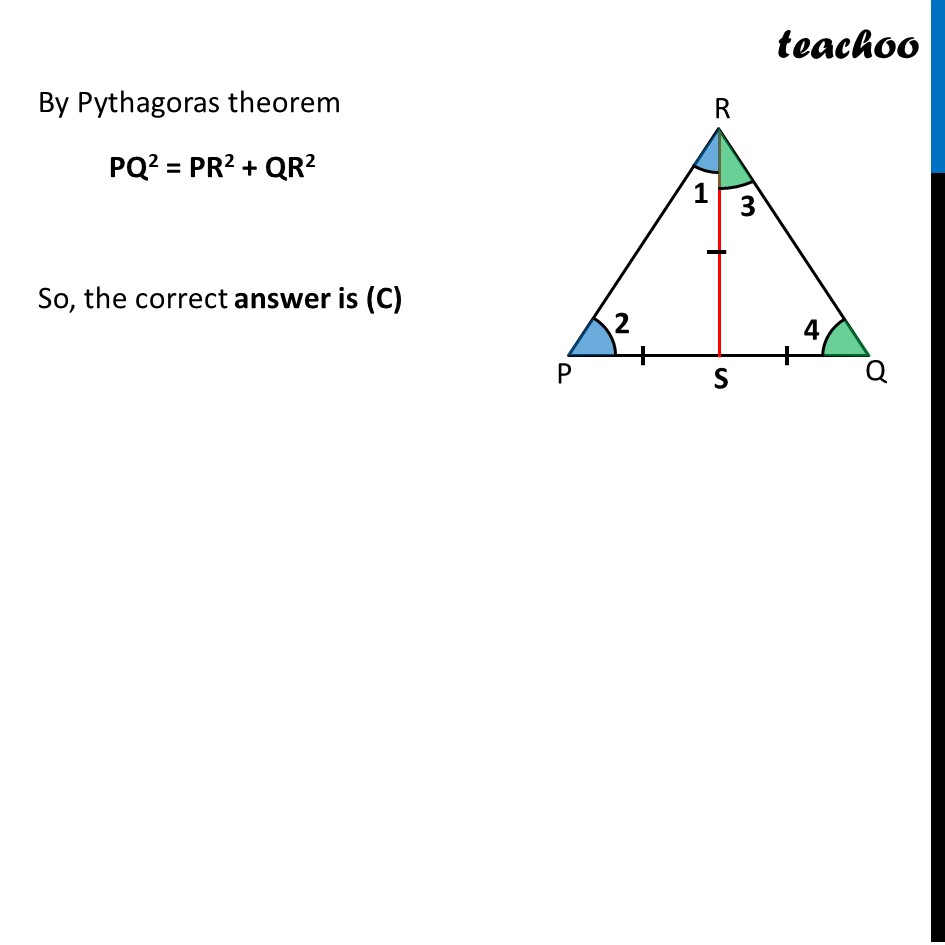
Question 14 If S is a point on side PQ of a ∆ PQR such that PS = QS = RS, then PR . QR = RS2 (B) QS2 + RS2 = QR2 (C) PR2 + QR2 = PQ2 (D) PS2 + RS2 = PR2 Given PS = QS = RS Now, We know that Angles opposite equal sides are equal In Δ PSR ∠ 1 = ∠ 2 In Δ QSR ∠ 3 = ∠ 4 In Δ PQR By Angle sum property ∠ P + ∠ Q + ∠ R = 180° ∠ 2 + ∠ 4 + (∠ 1 + ∠ 3) = 180° Putting ∠ 1 = ∠ 2 and ∠ 3 = ∠ 4 ∠ 1 + ∠ 3 + (∠ 1 + ∠ 3) = 180° 2(∠ 1 + ∠ 3) = 180° (∠ 1 + ∠ 3) = (180° )/2 (∠ 1 + ∠ 3) = 90° ∠ R = 90° Thus, Δ PRQ is a right angled triangle where ∠ R = 90° By Pythagoras theorem PQ2 = PR2 + QR2 So, the correct answer is (C)

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.