Question 7 - NCERT Exemplar - MCQ - Chapter 6 Class 10 Triangles

Last updated at August 14, 2026 by

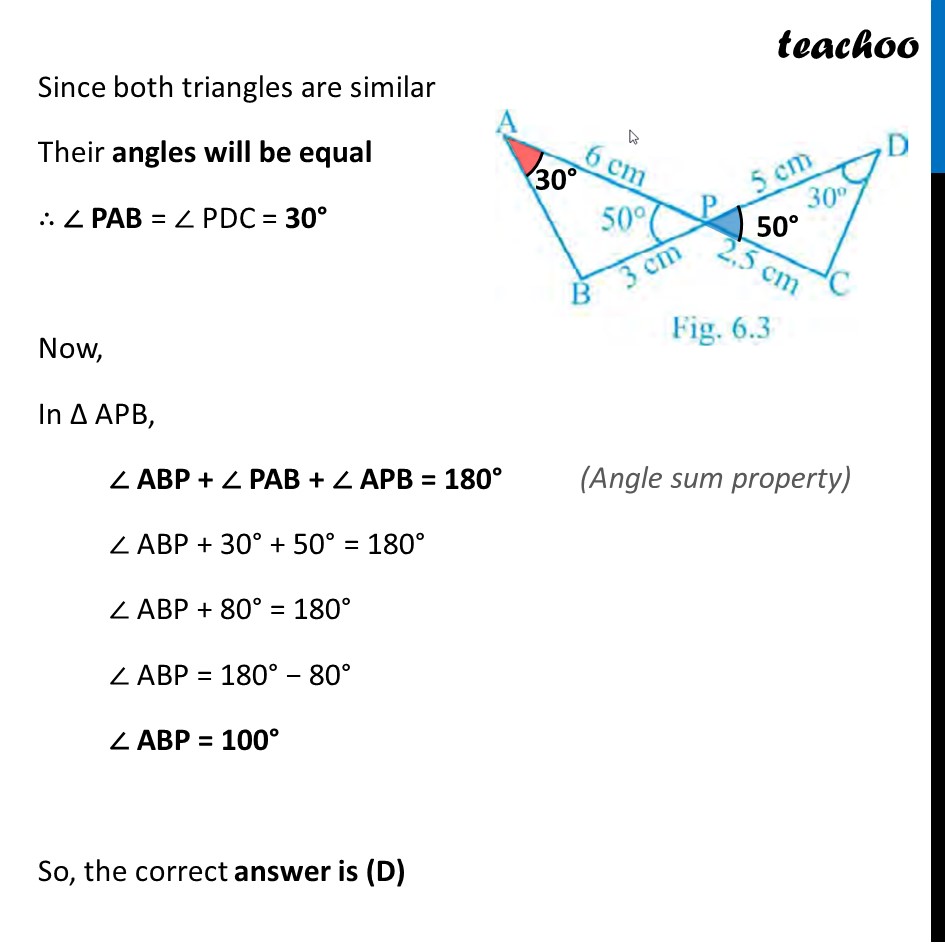
In Fig.6.3, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠ APB = 50° and ∠ CDP = 30°. Then, ∠ PBA is equal to

(A) 50°  (B) 30°   (C) 60°   (D) 100°

NCERT Exemplar [MCQ] - In Fig.6.3, two line segments AC and BD interse - NCERT Exemplar - MCQ

part 2 - Question 7 - NCERT Exemplar - MCQ - Serial order wise - Chapter 6 Class 10 Triangles

Take a fresh quiz. Then take another.
Every attempt is a new AI-adaptive Teachoo quiz with 3 questions, selected from your answers, mistakes, and progress.
Remove Ads
Teachoo · Class 10 Explore Class 10

Transcript

Question 7 In Fig.6.3, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠ APB = 50° and ∠ CDP = 30°. Then, ∠ PBA is equal to (A) 50° (B) 30° (C) 60° (D) 100° In Δ APB and Δ DPC 𝐴𝑃/𝐵𝑃=𝐷𝑃/𝐶𝑃 ∠ APB = ∠ DPC ∴ Δ APB ~ Δ DPC (Both ratios are same) (Vertically opposite angles) (SAS Similarity) Since both triangles are similar Their angles will be equal ∴ ∠ PAB = ∠ PDC = 30° Now, In Δ APB, ∠ ABP + ∠ PAB + ∠ APB = 180° ∠ ABP + 30° + 50° = 180° ∠ ABP + 80° = 180° ∠ ABP = 180° − 80° ∠ ABP = 100° So, the correct answer is (D) (Angle sum property)

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh is an IIT Kanpur graduate and has been teaching for 16+ years. At Teachoo, he breaks down Maths, Science and Computer Science into simple steps so students understand concepts deeply and score with confidence.

Many students prefer Teachoo Black for a smooth, ad-free learning experience.