Question 6 - Ratio of Area of Similar Triangles - Chapter 6 Class 10 Triangles

Last updated at Dec. 13, 2024 by

Ex 6.4, 6 - Prove that ratio of areas of two similar triangles - Area of similar triangles

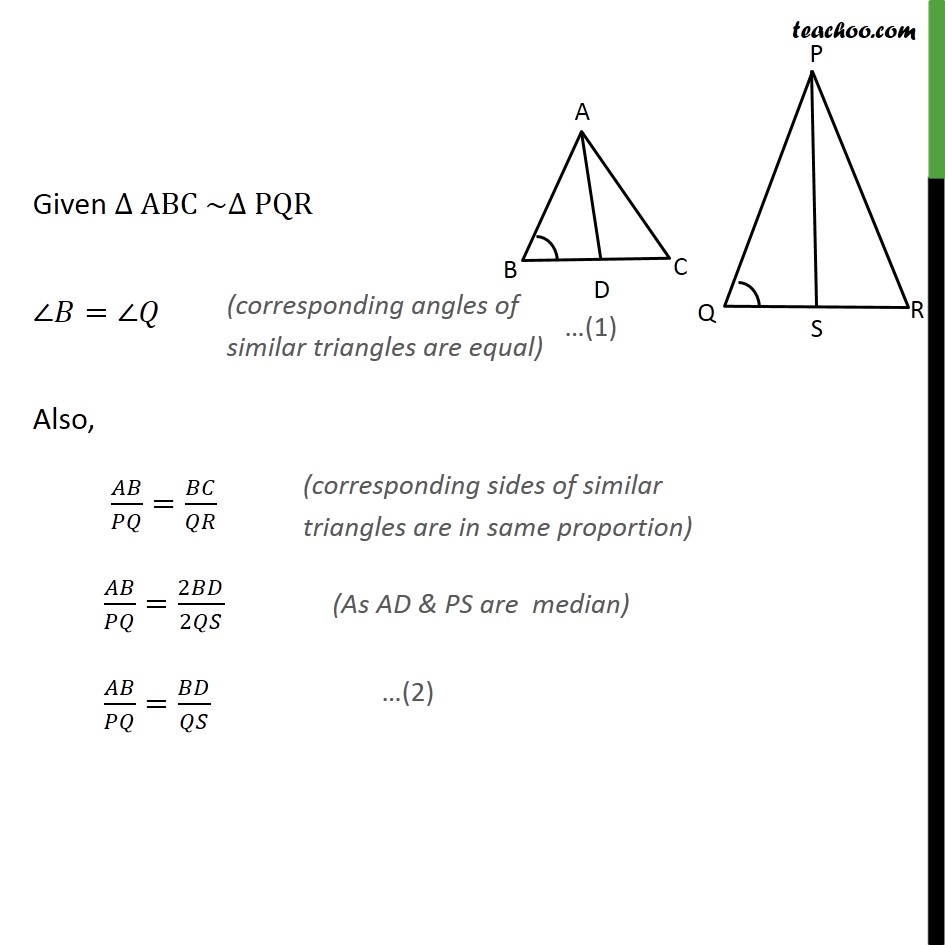
Ex 6.4, 6 - Chapter 6 Class 10 Triangles - Part 2
Ex 6.4, 6 - Chapter 6 Class 10 Triangles - Part 3

Go Ad-free

Transcript

Question 6 Exercise 6.4 Chapter 6 Class 10 CBSE NCERT Maths Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians. Given: Let ABC ~ PQR Here AD is median Hence BD = CD = 1/2 BC Similarly, PS is median Hence QS = RS = 1/2 QR To prove: ( )/( )=( / )^2 Proof: Given ABC ~ PQR = Also, / = / / =2 /2 / = / In & = / = / ~ Hence / = / Now, since ABC PQR We know that if two triangles are similar, the ratio of their area is always equal to the square of the ratio of their corresponding side ( )/( ) = ( / )^2 ( )/( ) = ( / )^2 Hence proved

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo