Ex 6.4, 7 - Chapter 6 Class 10 Triangles (Term 1)

Transcript

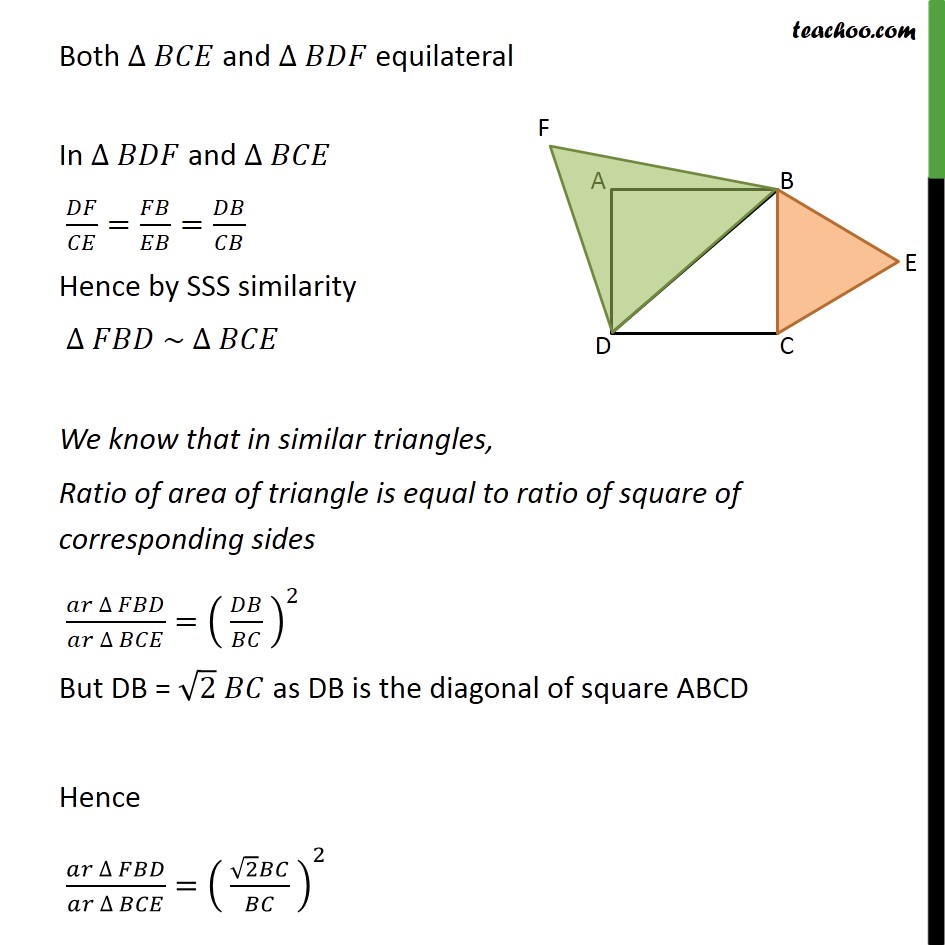
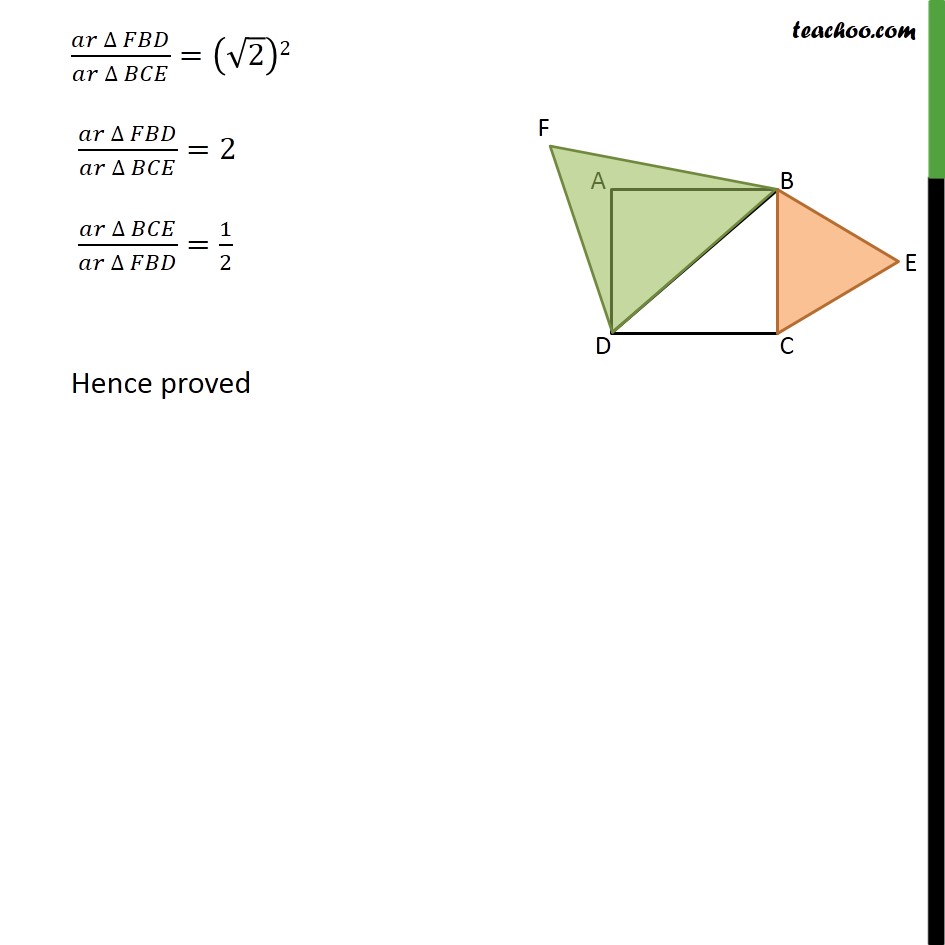
Ex 6.4, 7 (Introduction) Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals. Concept 1 Two equilateral triangle are always similar In ∆ 𝐴𝐵𝐶 𝑎𝑛𝑑 ∆ 𝐷𝐸𝐹 𝐷𝐸/𝐴𝐵=12/6 𝐸𝐹/𝐵𝐶=12/6 𝐷𝐹/𝐴𝐶=12/6 Hence by SSS similarity ∆ 𝐴𝐵𝐶 ~ ∆ 𝐷𝐸𝐹 Concept 2 Diagonal of a square is √2 of its side Since all sides of square are equal, Let AB = BC = CD = AD = x cm All angles of square are 90° So, ∠ C = 90° According to Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 (BD)2 = BC2 + DC2 (BD)2 = BC2 + DC2 BD2 = x2 + x2 BD2 = 2x2 BD = √2 x Hence, 𝐷𝑖𝑎𝑔𝑜𝑛𝑎𝑙/𝑠𝑖𝑑𝑒 = 𝐵𝐷/𝐷𝐶 = (√2 𝑥)/𝑥 = √2/1 Diagonal = √2 side Now we can apply these concepts in Ex 6.4, 7 Ex 6.4, 7 Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals. Given: Square ABCD with Diagonal BD ∆ 𝐵𝐶𝐸 which is described on base BC ∆ 𝐵𝐷𝐹 which is descried on base BD Both ∆ 𝐵𝐶𝐸 and ∆ 𝐵𝐷𝐹 equilateral To prove: (𝑎𝑟 ∆ 𝐵𝐶𝐸)/(𝑎𝑟 ∆ 𝐹𝐷𝐵)=1/2 Proof: Both Δ 𝐵𝐶𝐸 and ∆ 𝐵𝐷𝐹 equilateral Both ∆ 𝐵𝐶𝐸 and ∆ 𝐵𝐷𝐹 equilateral In ∆ 𝐵𝐷𝐹 and ∆ 𝐵𝐶𝐸 𝐷𝐹/𝐶𝐸=𝐹𝐵/𝐸𝐵=𝐷𝐵/𝐶𝐵 Hence by SSS similarity ∆ 𝐹𝐵𝐷 ~ ∆ 𝐵𝐶𝐸 We know that in similar triangles, Ratio of area of triangle is equal to ratio of square of corresponding sides (𝑎𝑟 ∆ 𝐹𝐵𝐷)/(𝑎𝑟 ∆ 𝐵𝐶𝐸)=( 𝐷𝐵/𝐵𝐶 )^2 But DB = √2 𝐵𝐶 as DB is the diagonal of square ABCD Hence (𝑎𝑟 ∆ 𝐹𝐵𝐷)/(𝑎𝑟 ∆ 𝐵𝐶𝐸)=( (√2 𝐵𝐶)/𝐵𝐶 )^2 (𝑎𝑟 ∆ 𝐹𝐵𝐷)/(𝑎𝑟 ∆ 𝐵𝐶𝐸)=(√2)2 (𝑎𝑟 ∆ 𝐹𝐵𝐷)/(𝑎𝑟 ∆ 𝐵𝐶𝐸)=2 (𝑎𝑟 ∆ 𝐵𝐶𝐸)/(𝑎𝑟 ∆ 𝐹𝐵𝐷)=1/2 Hence proved