CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard
You are here
CBSE Class 10 Sample Paper for 2025 Boards - Maths Standard
Last updated at Feb. 12, 2025 by Teachoo
Transcript
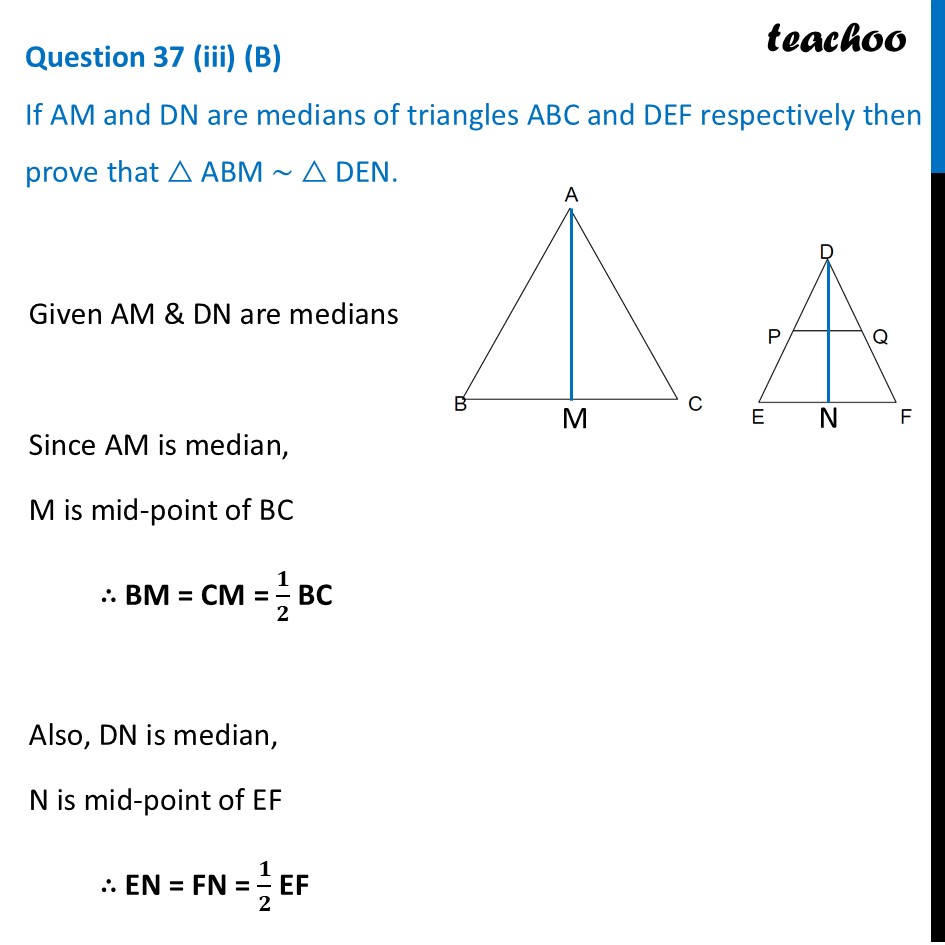
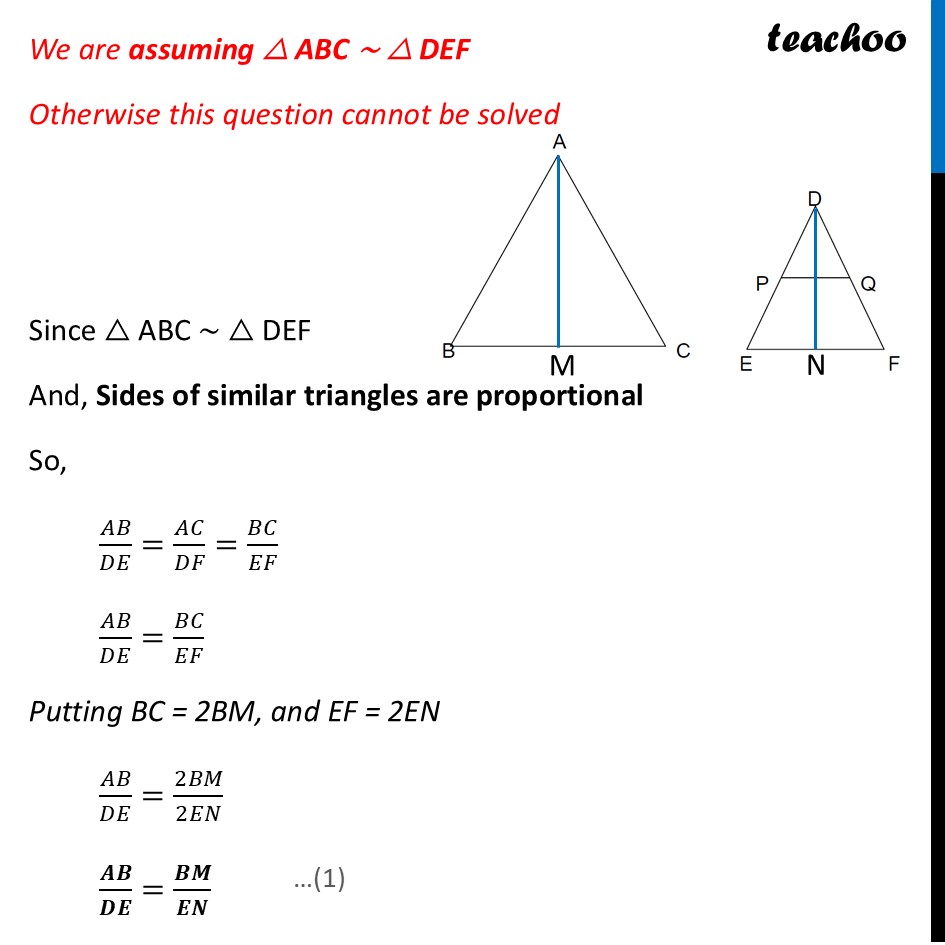
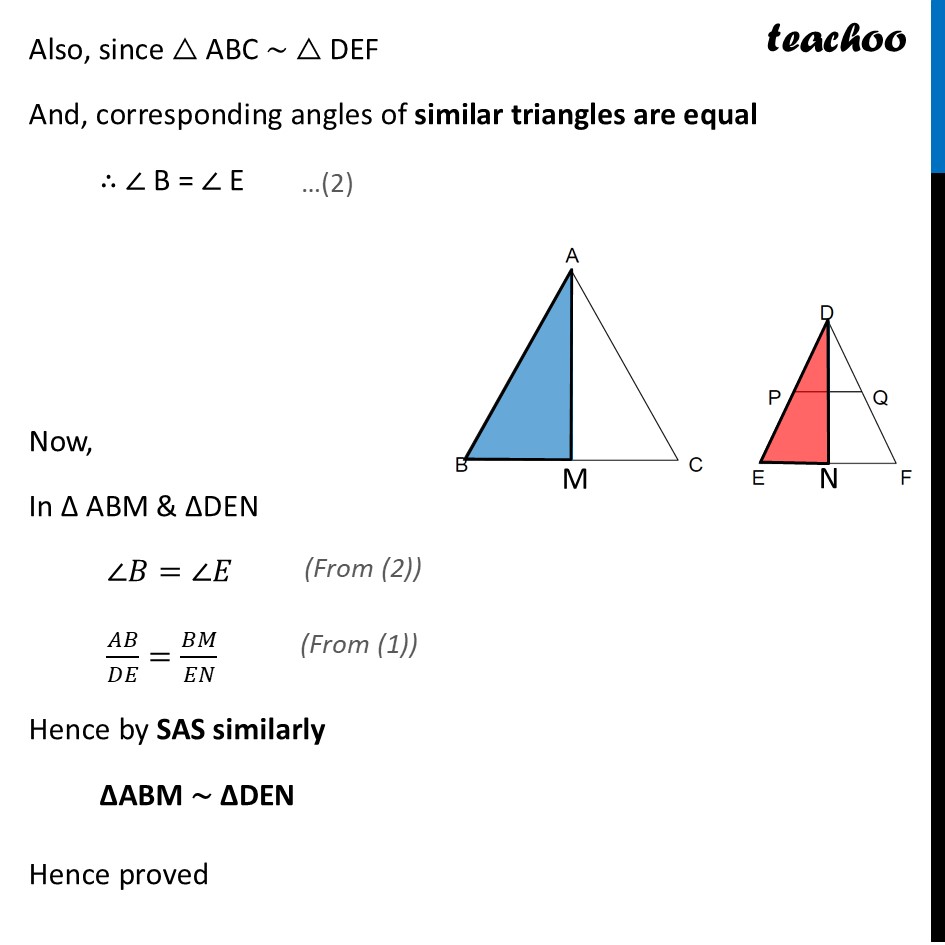
Question 37 (iii) (B) If AM and DN are medians of triangles ABC and DEF respectively then prove that △ ABM ∼ △ DEN.Given AM & DN are medians Since AM is median, M is mid-point of BC ∴ BM = CM = 𝟏/𝟐 BC Also, DN is median, N is mid-point of EF ∴ EN = FN = 𝟏/𝟐 EF We are assuming △ ABC ∼ △ DEF Otherwise this question cannot be solved Since △ ABC ∼ △ DEF And, Sides of similar triangles are proportional So, 𝐴𝐵/𝐷𝐸=𝐴𝐶/𝐷𝐹=𝐵𝐶/𝐸𝐹 𝐴𝐵/𝐷𝐸=𝐵𝐶/𝐸𝐹 Putting BC = 2BM, and EF = 2EN 𝐴𝐵/𝐷𝐸=2𝐵𝑀/2𝐸𝑁 𝑨𝑩/𝑫𝑬=𝑩𝑴/𝑬𝑵 Also, since △ ABC ∼ △ DEF And, corresponding angles of similar triangles are equal ∴ ∠ B = ∠ E Now, In Δ ABM & ΔDEN ∠𝐵=∠𝐸 𝐴𝐵/𝐷𝐸=𝐵𝑀/𝐸𝑁 Hence by SAS similarly ΔABM ∼ ΔDEN Hence proved
