Example 8 - Chapter 6 Class 10 Triangles (Term 1)

Transcript

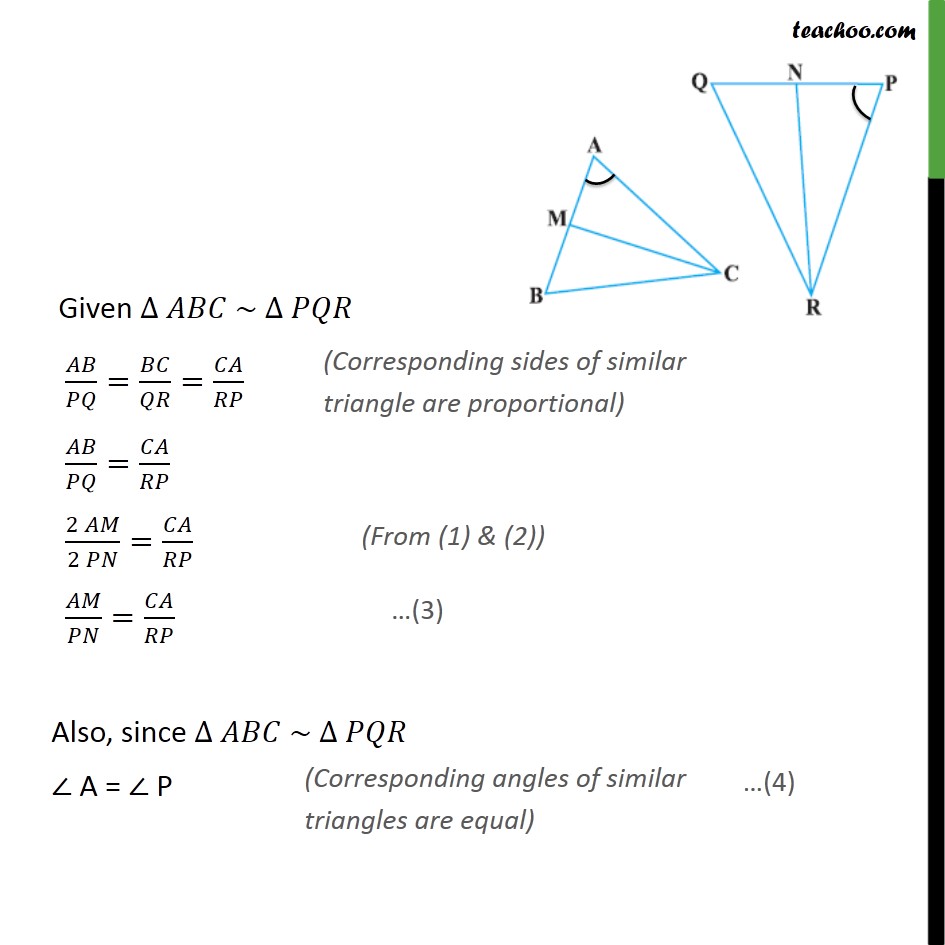
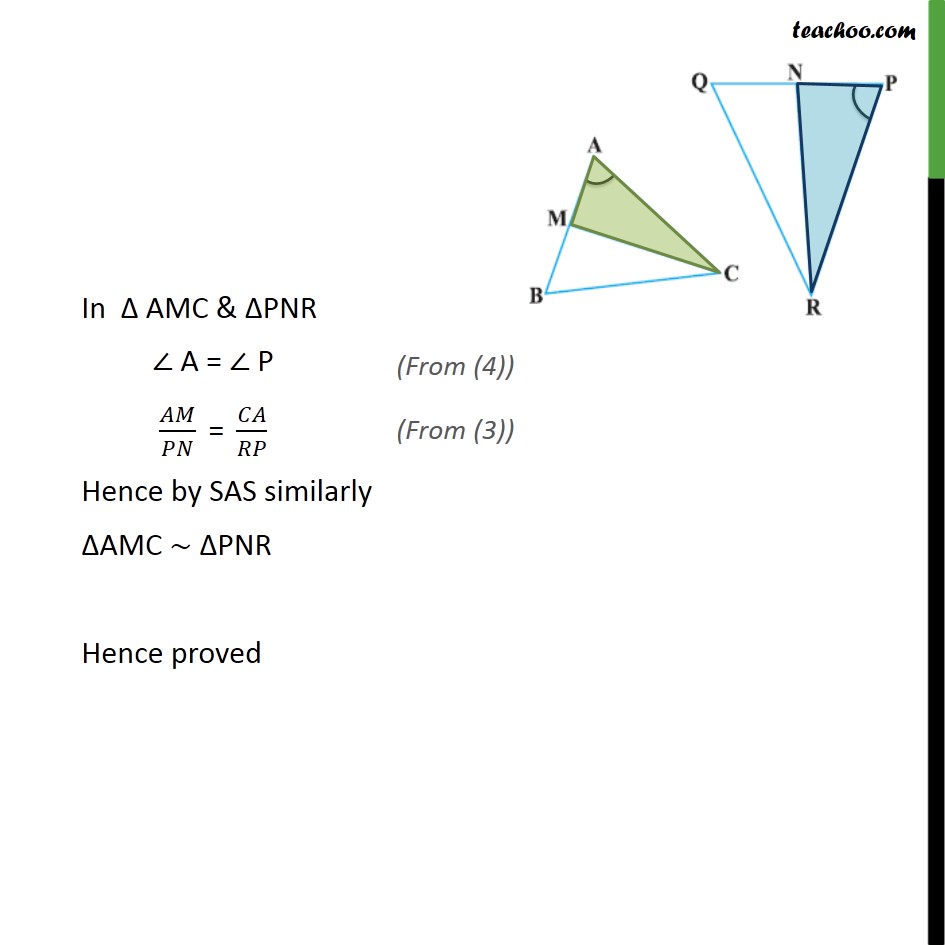
Example 8 In Fig. 6.33, CM and RN are respectively the medians of Δ ABC and Δ PQR. If Δ ABC ~ Δ PQR, prove that : (i) Δ AMC ~ Δ PNR Given: Δ ABC and Δ PQR CM is the median of Δ ABC and RN is the median of Δ PQR Also , Δ ABC ~ Δ PQR To Prove: Δ AMC ~ Δ PNR Proof: CM is median of Δ ABC So, AM = MB = 1/2 AB Similarly, RN is the median of Δ PQR So, PN = QN = 1/2 PQ Given ∆ 𝐴𝐵𝐶 ~ ∆ 𝑃𝑄𝑅 𝐴𝐵/𝑃𝑄=𝐵𝐶/𝑄𝑅=𝐶𝐴/𝑅𝑃 𝐴𝐵/𝑃𝑄=𝐶𝐴/𝑅𝑃 (2 𝐴𝑀)/(2 𝑃𝑁)=𝐶𝐴/𝑅𝑃 𝐴𝑀/𝑃𝑁=𝐶𝐴/𝑅𝑃 Also, since ∆ 𝐴𝐵𝐶 ~ ∆ 𝑃𝑄𝑅 ∠ A = ∠ P In Δ AMC & ΔPNR ∠ A = ∠ P 𝐴𝑀/𝑃𝑁 " = " 𝐶𝐴/𝑅𝑃 Hence by SAS similarly ΔAMC ∼ ΔPNR Hence proved Example 8 In Fig. 6.33, CM and RN are respectively the medians of Δ ABC and Δ PQR. If Δ ABC ~ Δ PQR, prove that : (ii) 𝐶𝑀/𝑅𝑁=𝐴𝐵/𝑃𝑄 In part (i) we proved that Δ AMC ~ Δ PNR So, 𝐶𝑀/𝑅𝑁=𝐴𝐶/𝑃𝑅= 𝐴𝑀/𝑃𝑁 Therefore, 𝐶𝑀/𝑅𝑁= 𝐴𝑀/𝑃𝑁 𝐶𝑀/𝑅𝑁= 2𝐴𝑀/2𝑃𝑁 𝐶𝑀/𝑅𝑁=𝐴𝐵/𝑃𝑄 Hence Proved Example 8 In Fig. 6.33, CM and RN are respectively the medians of Δ ABC and Δ PQR. If Δ ABC ~ Δ PQR, prove that : (iii) Δ CMB ~ Δ RNQ Given ∆ 𝐴𝐵𝐶 ~ ∆ 𝑃𝑄𝑅 𝐴𝐵/𝑃𝑄=𝐵𝐶/𝑄𝑅=𝐶𝐴/𝑅𝑃 𝐴𝐵/𝑃𝑄=𝐵𝐶/𝑄𝑅 (2 𝐵𝑀)/(2 𝑄𝑁)=𝐵𝐶/𝑄𝑅 𝐵𝑀/𝑄𝑁=𝐵𝐶/𝑄𝑅 Also, since ∆ 𝐴𝐵𝐶 ~ ∆ 𝑃𝑄𝑅 ∠ B = ∠ Q Now in Δ CMB & ΔRNQ ∠𝐵=∠𝑄 𝐵𝑀/𝑄𝑁=𝐵𝐶/𝑄𝑅 Hence by SAS similarly ΔCMB ∼ ΔRNQ Hence proved