Example 2 - Chapter 6 Class 10 Triangles

Transcript

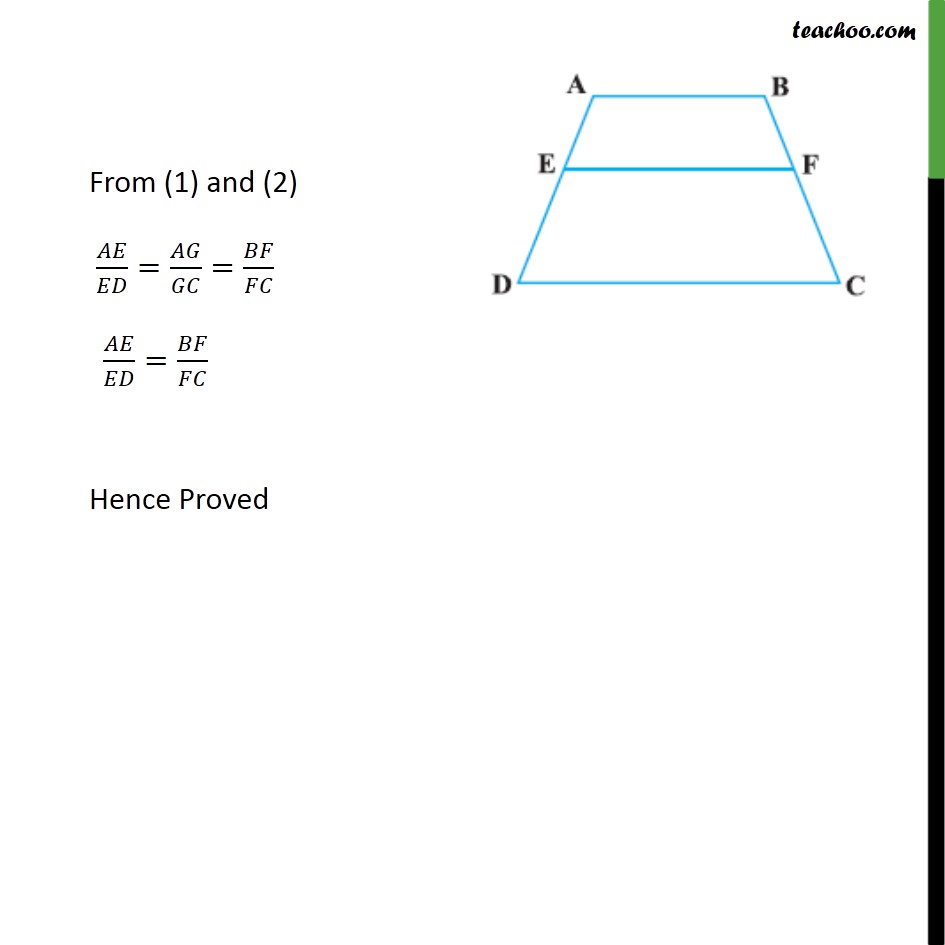
Example 2 ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB (see Fig. 6.14). Show that 𝐴𝐸/𝐸𝐷 = 𝐵𝐹/𝐹𝐶 Given: ABCD is a trapezium where AB II DC E and F are points non parallel sides AD and BC such that EF II AB To Prove: 𝐴𝐸/𝐸𝐷=𝐵𝐹/𝐹𝐶 Proof: Given AB II DC & EF II AD So, EF II DC Joining A & C Let AC intersect EF at point G Now in ∆ 𝐴𝐷𝐶 EG II DC So, 𝐴𝐸/𝐸𝐷=𝐴𝐺/𝐺𝐶 Similarly , in ∆ 𝐶𝐴𝐵 AB II GF So, 𝐴𝐺/𝐺𝐶=𝐵𝐹/𝐹𝐶 From (1) and (2) 𝐴𝐸/𝐸𝐷=𝐴𝐺/𝐺𝐶=𝐵𝐹/𝐹𝐶 𝐴𝐸/𝐸𝐷=𝐵𝐹/𝐹𝐶 Hence Proved