Ex 6.5, 16 - Chapter 6 Class 10 Triangles

Transcript

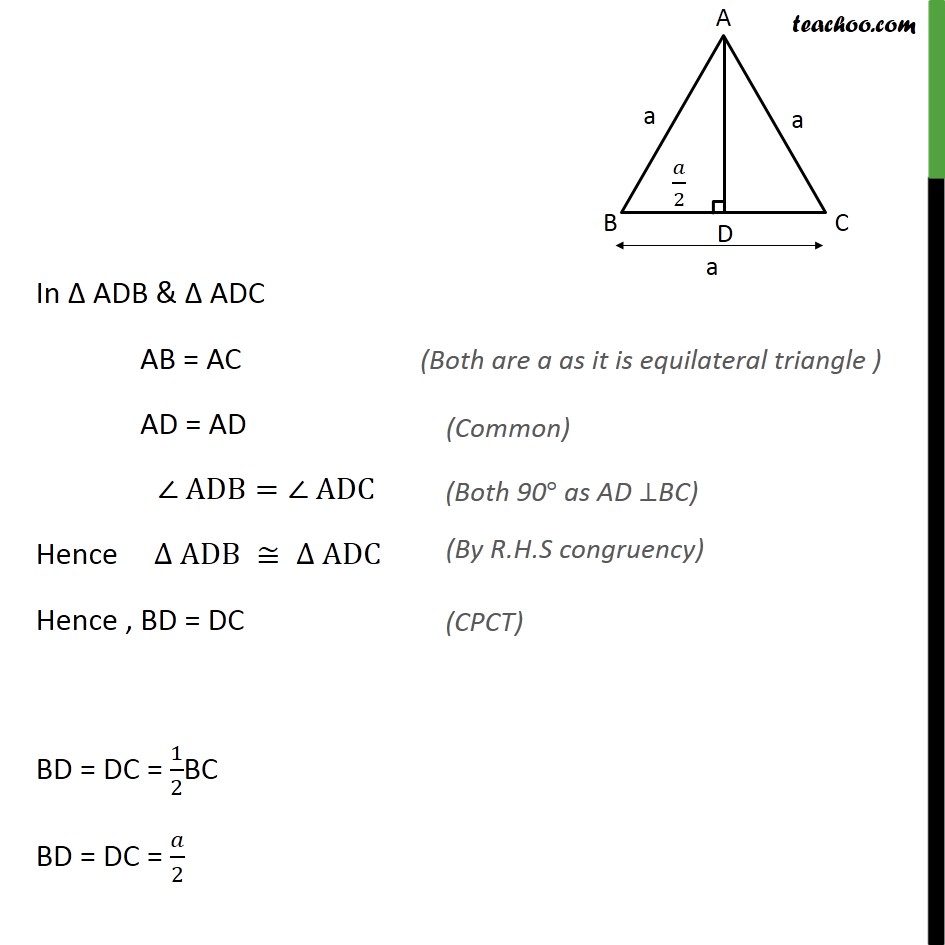
Ex 6.5, 16 In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes. Given:- Equilateral triangle ABC with each side a & AD as one of its altitudes To Prove :- 3 × Square of one side = 4 × square of one of it’s altitude ⇒ 3a2 = 4AD2 Proof:- In Δ ADB & Δ ADC AB = AC AD = AD ∠ ADB=∠ ADC Hence ∆ ADB ≅ ∆ ADC Hence , BD = DC BD = DC = 1/2BC BD = DC = 𝑎/2 Now, ADB is a right angle triangle Using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 (AB)2 = (AD)2 + (BD)2 (a)2 = AD2 + (1/2 𝑎)2 a2 = AD2 + 𝑎2/4 a2 – 𝑎2/4=𝐴𝐷2 (4𝑎2 − 𝑎2)/4=𝐴𝐷2 3𝑎2/4=𝐴𝐷2 3a2 = 4 ×𝐴𝐷2 3a2 = 4AD2 Hence proved