Question 11 - Pythagoras Theorem and it's important questions - Chapter 6 Class 10 Triangles

Transcript

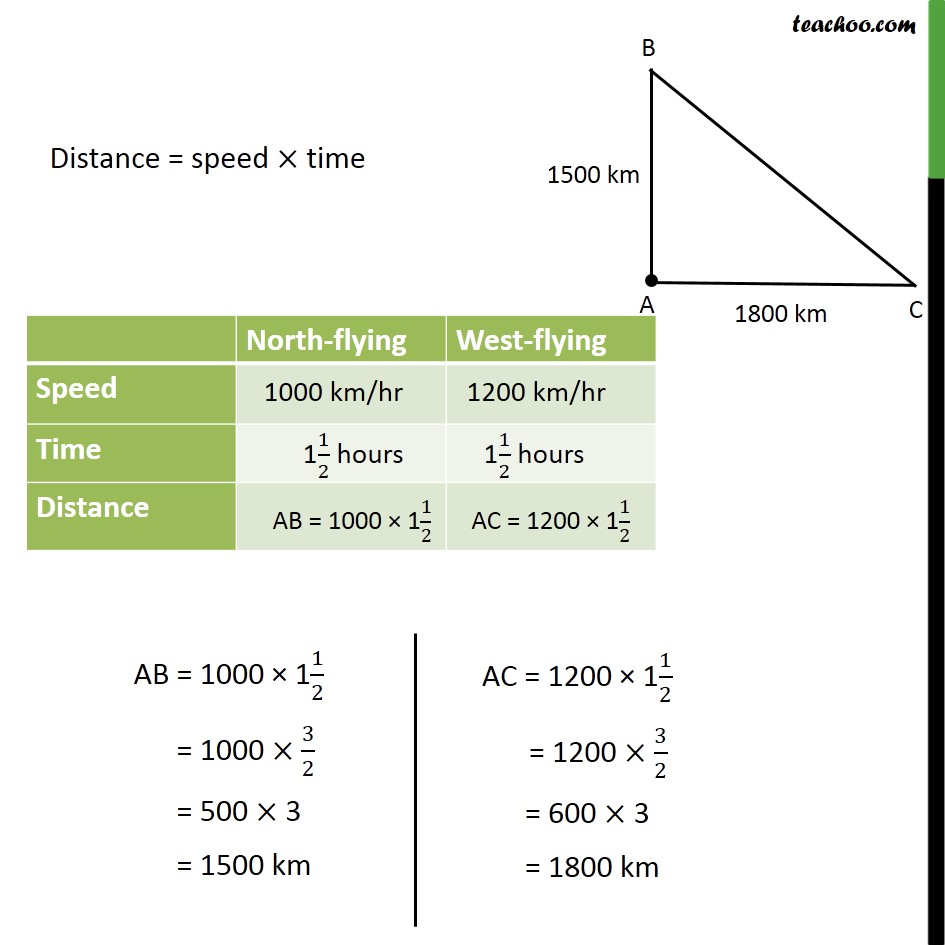
Question 11 An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 11/2 hours? Given : Speed of north flying aeroplane = 1000 km/hr. Speed of west-flying aeroplane = 1200 km/hr. To find: Distance between the two planes after 1.5 hours , i.e. , BC Solution: We know that Speed = (𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒 )/𝑇𝑖𝑚𝑒 Distance = speed × time Now, we have to find distance BC Since North and West are perpendicular, ∠ BAC = 90° So, Δ ABC is a right triangle Using Pythagoras theorem in right angle triangle ACB (Hypotenuse)2 = (Height)2 + (Base)2 (BC)2 = (AB)2 + (AC)2 (BC)2 = (1500)2 + (1800)2 (BC)2 = 2250000 + 3240000 (BC) = √5490000 = √(3×3×61×100×100) = √((3)^2×(100)^2 )×√61 = 3×100√61 = 300 √61 km Hence, two planes would be 300√61 km from each other.