Ex 6.3, 12 - Chapter 6 Class 10 Triangles

Last updated at Dec. 13, 2024 by

Ex 6.3, 12 - Sides AB and BC and median AD of a ABC - Ex 6.3

Ex 6.3, 12 - Chapter 6 Class 10 Triangles - Part 2

Share on WhatsApp

Transcript

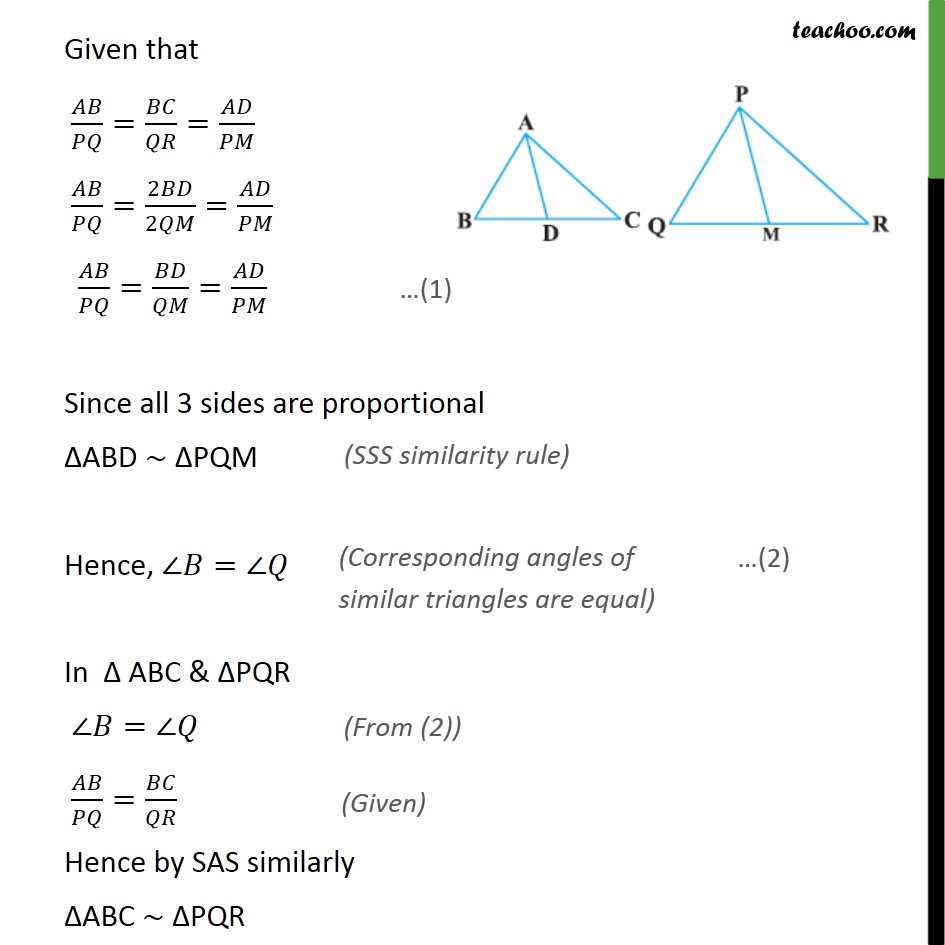
Ex 6.3, 12 Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of PQR (see figure). Show that ABC PQR. Given: ABC where AD is the median PQR where PM is the median & / = / = / To Prove: ABC PQR. Proof:- Since AD is the median, BD = CD = 1/2 BC Similarly, PM is the median, QM = RM = 1/2QR Given that / = / = / / =2 /2 = / / = / = / Since all 3 sides are proportional ABD PQM Hence, = In ABC & PQR = / = / Hence by SAS similarly ABC PQR

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo