Ex 6.3, 10 - Chapter 6 Class 10 Triangles

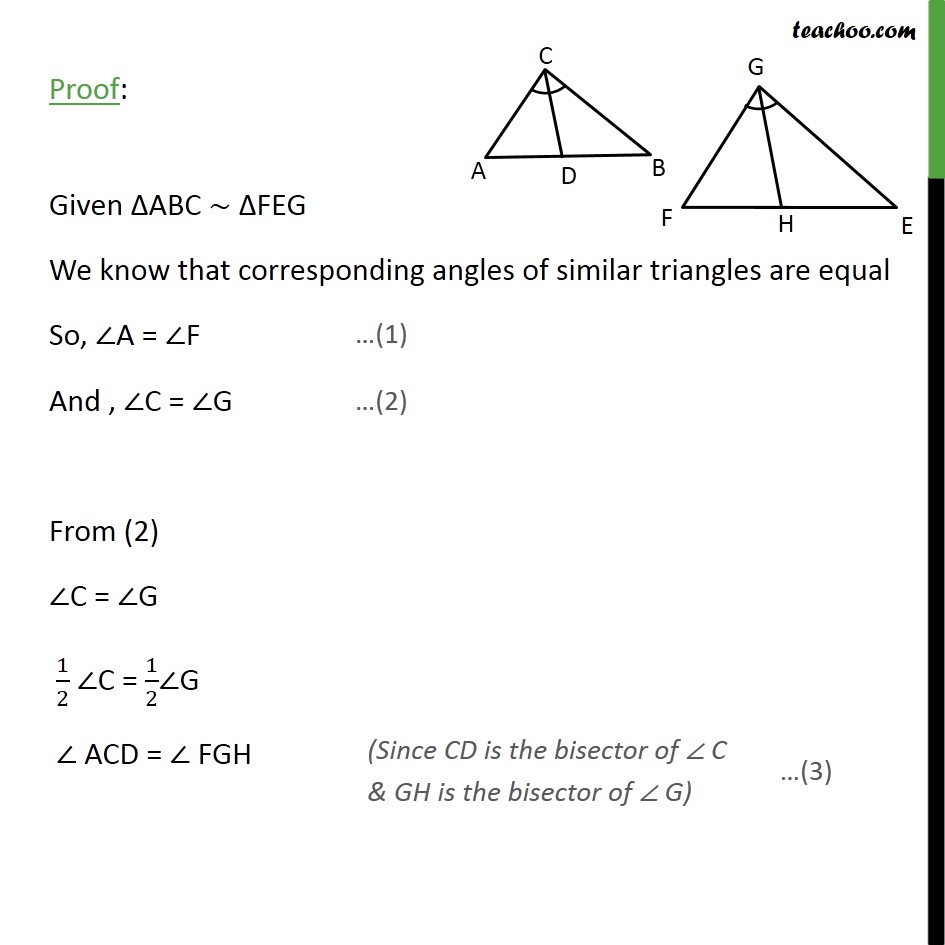
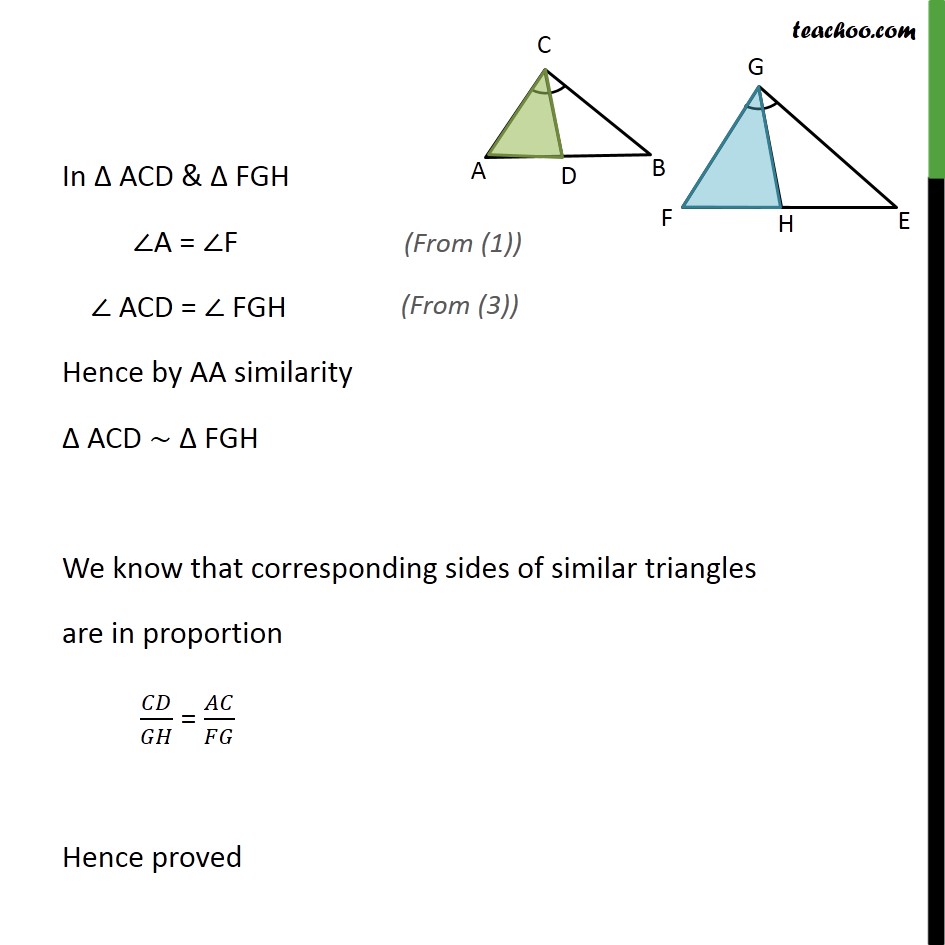
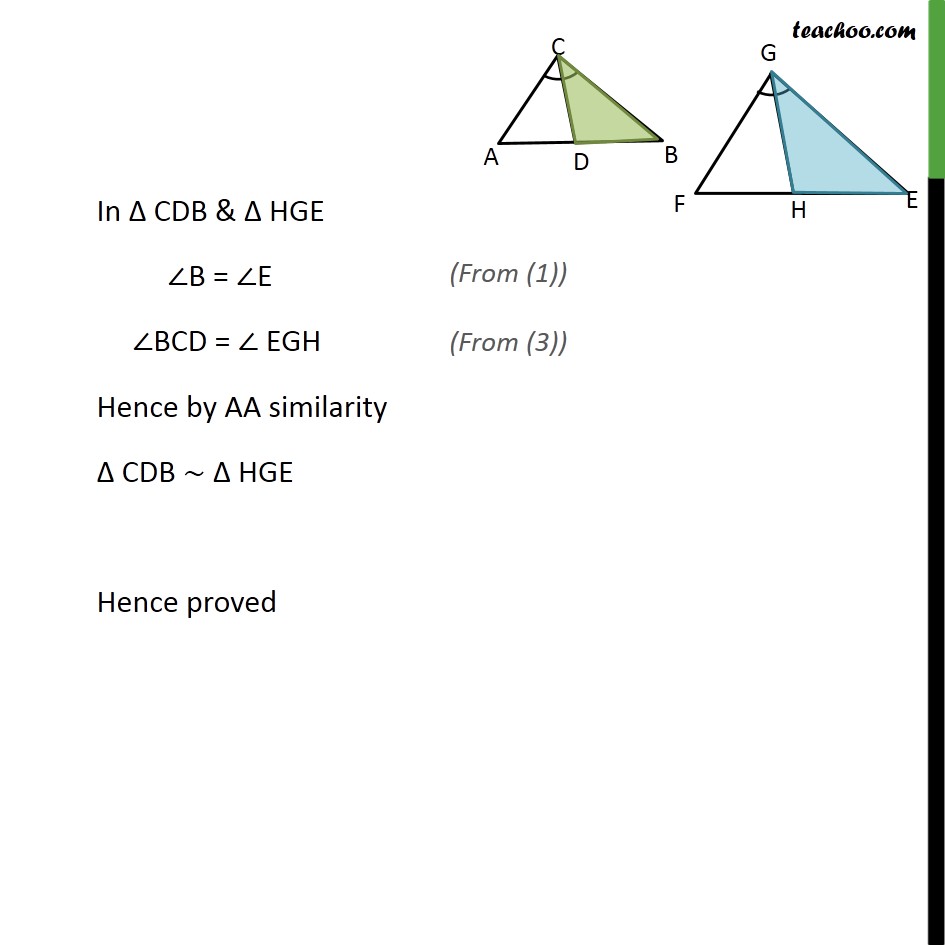
Transcript

Ex 6.3, 10 CD and GH are respectively the bisectors of ACB and EGF such that D and H lie on sides AB and FE of ABC and EFG respectively. If ABC FEG, show that: / = / Given: ACB and EGF respectively And , CD is the bisectors of ACB ACD = BCD = 1/2 ACB & GH is the bisectors of EGF FGH = EGH = 1/2 EGF & ABC FEG To Prove: / = / Proof: Given ABC FEG We know that corresponding angles of similar triangles are equal So, A = F And , C = G From (2) C = G 1/2 C = 1/2 G ACD = FGH In ACD & FGH A = F ACD = FGH Hence by AA similarity ACD FGH We know that corresponding sides of similar triangles are in proportion / = / Hence proved Ex 6.3, 10 CD and GH are respectively the bisectors of ACB and EGF such that D and H lie on sides AB and FE of ABC and EFG respectively. If ABC FEG, show that: (ii) DCB HGE Given ABC FEG We know that corresponding angles of similar triangles are equal So, B = E And , C = G From (2) C = G 1/2 C = 1/2 G BCD = EGH In CDB & HGE B = E BCD = EGH Hence by AA similarity CDB HGE Hence proved Ex 6.3, 10 CD and GH are respectively the bisectors of ACB and EGF such that D and H lie on sides AB and FE of ABC and EFG respectively. If ABC FEG, show that: (iii) DCA HGF Given ABC FEG We know that corresponding angles of similar triangles are equal So, A = F And , C = G From (2) C = G 1/2 C = 1/2 G ACD = FGH In ACD & FGH A = F ACD = FGH Hence by AA similarity ACD FGH Hence proved