Question 34 (Choice 1) - CBSE Class 12 Sample Paper for 2021 Boards

Transcript

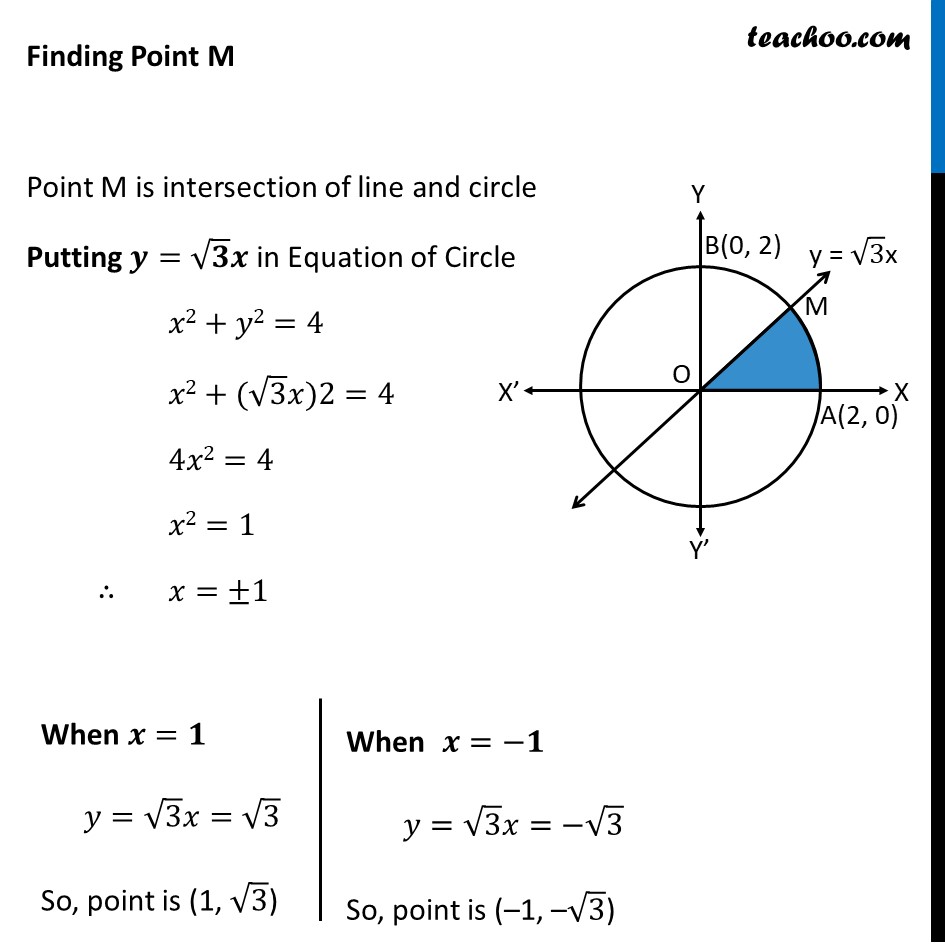
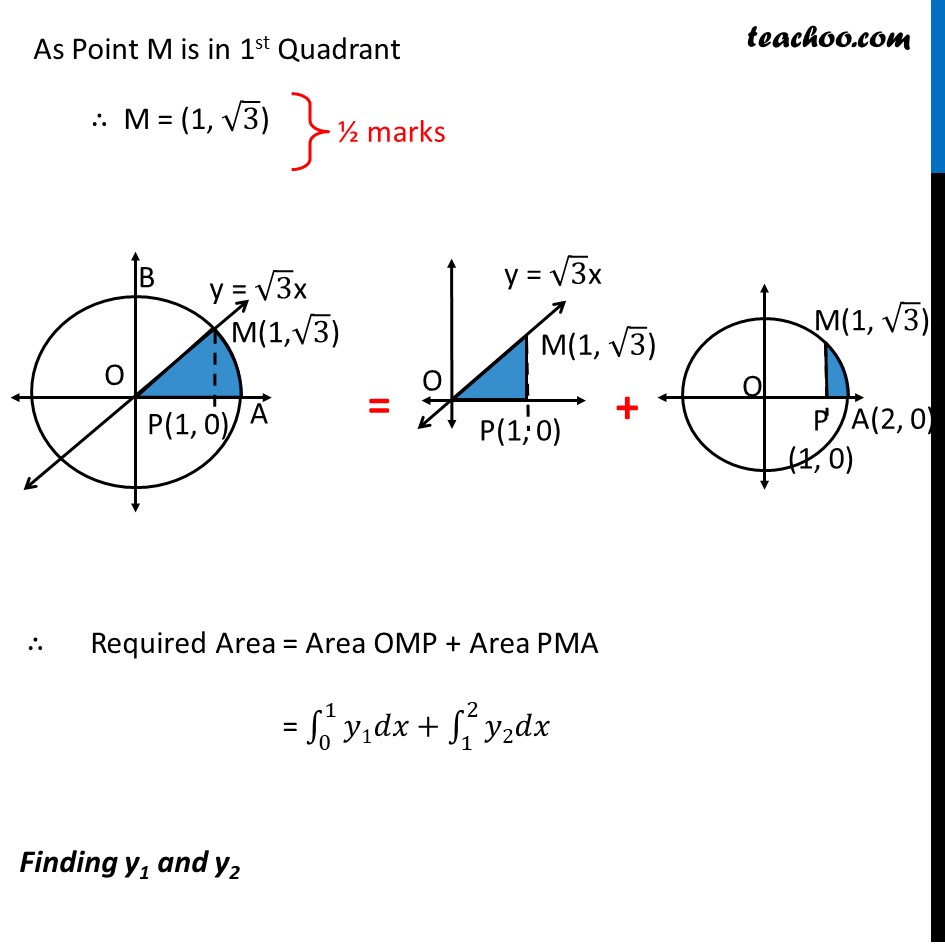
Question 34 (Choice 1) Find the area of the region bounded by the curves 𝑥^2+𝑦^2=4, 𝑦=√3 𝑥 𝑎𝑛𝑑 𝑥 − 𝑎𝑥𝑖𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑑𝑟𝑎𝑛𝑡 Given Equation of Circle 𝑥2+𝑦2=4 𝑥2+𝑦2=2^2 So, Radius = 2 ∴ Point A (2, 0) and B is (0, 2) Let point where line and circle intersect be point M Required Area = Area of shaded region = Area OMA Finding Point M Point M is intersection of line and circle Putting 𝒚=√𝟑 𝒙 in Equation of Circle 𝑥2+𝑦2=4 𝑥2+(√3 𝑥)2=4 4𝑥2=4 𝑥2=1 ∴ 𝑥=±1 When 𝒙=𝟏 𝑦=√3 𝑥=√3 So, point is (1, √3) When 𝒙=−𝟏 𝑦=√3 𝑥=−√3 So, point is (–1, –√3) As Point M is in 1st Quadrant ∴ M = (1, √3) ∴ Required Area = Area OMP + Area PMA = ∫1_0^1▒𝑦1𝑑𝑥+∫1_1^2▒𝑦2𝑑𝑥 Finding y1 and y2 For y1 – Equation of Line y = √3x So, y1 = √3x For y2 – Equation of Circle 𝑥^2+𝑦^2=4 𝑦^2=4−𝑥^2 ∴ 𝑦=±√(2^2−𝑥^2 ) As Required Area is in first Quadrant ∴ 𝑦2=√(2^2−𝑥^2 ) Thus, Required Area = ∫1_0^1▒〖√3 𝑥 𝑑𝑥〗+∫1_1^2▒〖√(2^2−𝑥^2 ) 𝑑𝑥〗 =√3 ∫1_0^1▒〖𝑥 𝑑𝑥〗+∫1_1^2▒〖√(2^2−𝑥^2 ) 𝑑𝑥〗 =√3 [𝑥^2/2]_0^1+∫1_1^2▒〖√(2^2−𝑥^2 ) 𝑑𝑥〗 =√3 [1^2/2−0^2/2]_0^1+∫1_1^2▒〖√(2^2−𝑥^2 ) 𝑑𝑥〗 =√3/2+∫1_1^2▒〖√(2^2−𝑥^2 ) 𝑑𝑥〗 It is of form ∫1▒〖√(𝑎^2−𝑥^2 ) 𝑑𝑥=1/2 𝑥√(𝑎^2−𝑥^2 )〗+𝑎^2/2 〖𝑠𝑖𝑛〗^(−1)⁡〖𝑥/𝑎+𝑐〗 Replacing a by 2 , we get 〖=√3/2+[𝑥/2 √((2)^2−𝑥^2 )+(2)^2/2 sin^(−1)⁡〖𝑥/2〗 ]〗_1^2 =√3/2+2/2 √((2)^2−(2)^2 )+2 sin^(−1)⁡〖2/2〗−1/2 √((2)^2−("1" )^2 )−2 sin^(−1)⁡〖1/2〗 =√3/2+0+2 sin^(−1)⁡〖(1)−1/2 √(4−1)−〗 2 sin^(−1)⁡(1/2) =√3/2+2 ×𝜋/2−√3/2−2×𝜋/6 =𝜋 −𝜋/3 =𝟐𝝅/𝟑 square units