CBSE Class 12 Sample Paper for 2021 Boards
You are here
CBSE Class 12 Sample Paper for 2021 Boards
Last updated at Dec. 16, 2024 by Teachoo
Transcript
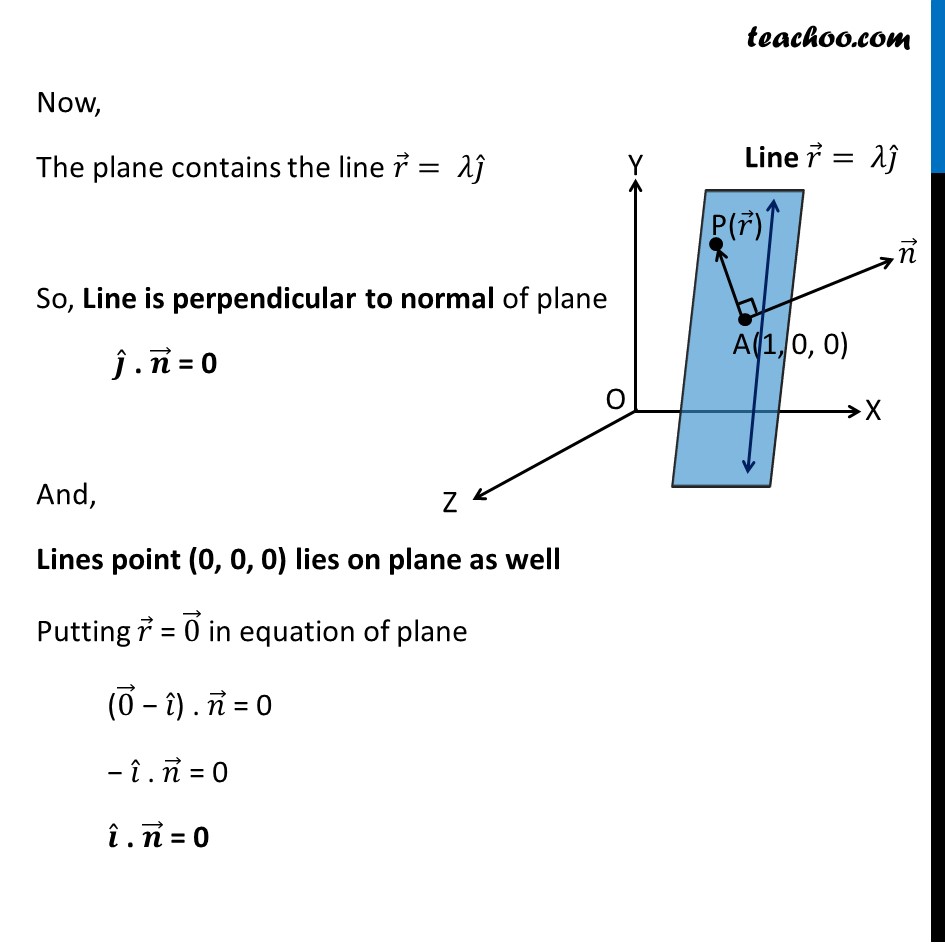
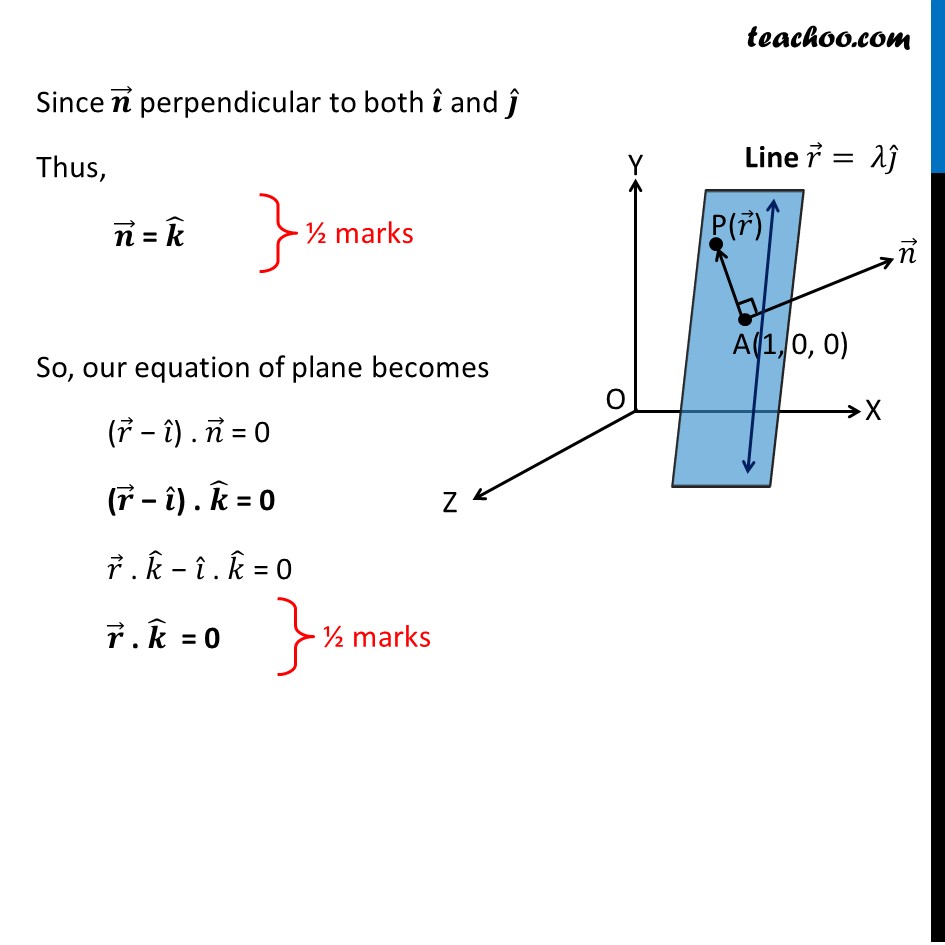
Equation of plane passing through point A whose position vector is 𝒂 ⃗ & perpendicular to 𝒏 ⃗ is (𝒓 ⃗ − 𝒂 ⃗) . 𝒏 ⃗ = 0 Given Plane passes through (1, 0, 0) So 𝒂 ⃗ = 1𝑖 ̂ + 0𝑗 ̂ − 0𝑘 ̂ 𝒂 ⃗ = 𝑖 ̂ Thus, equation of plane is (𝑟 ⃗ − 𝑎 ⃗) . 𝑛 ⃗ = 0 (𝒓 ⃗ − 𝒊 ̂) . 𝒏 ⃗ = 0 Now, The plane contains the line 𝑟 ⃗= 𝜆𝑗 ̂ So, Line is perpendicular to normal of plane 𝒋 ̂ . 𝒏 ⃗ = 0 And, Lines point (0, 0, 0) lies on plane as well Putting 𝑟 ⃗ = 0 ⃗ in equation of plane (0 ⃗ − 𝑖 ̂) . 𝑛 ⃗ = 0 − 𝑖 ̂ . 𝑛 ⃗ = 0 𝒊 ̂ . 𝒏 ⃗ = 0 Since 𝒏 ⃗ perpendicular to both 𝒊 ̂ and 𝒋 ̂ Thus, 𝒏 ⃗ = 𝒌 ̂ So, our equation of plane becomes (𝑟 ⃗ − 𝑖 ̂) . 𝑛 ⃗ = 0 (𝒓 ⃗ − 𝒊 ̂) . 𝒌 ̂ = 0 𝑟 ⃗ . 𝑘 ̂ − 𝑖 ̂ . 𝑘 ̂ = 0 𝒓 ⃗ . 𝒌 ̂ = 0
