Question 8 (MCQ) - Approximations (using Differentiation) - Chapter 6 Class 12 Application of Derivatives
Last updated at Dec. 16, 2024 by Teachoo
Approximations (using Differentiation)
Question 1 (i)
Important
You are here
You are here
Chapter 6 Class 12 Application of Derivatives
Serial order wise
- Ex 6.1
- Ex 6.2
- Ex 6.3
- Examples
- Miscellaneous
- Case Based Questions (MCQ)
- NCERT Exemplar - MCQs
- Tangents and Normals (using Differentiation)
-
Approximations (using Differentiation)
Transcript
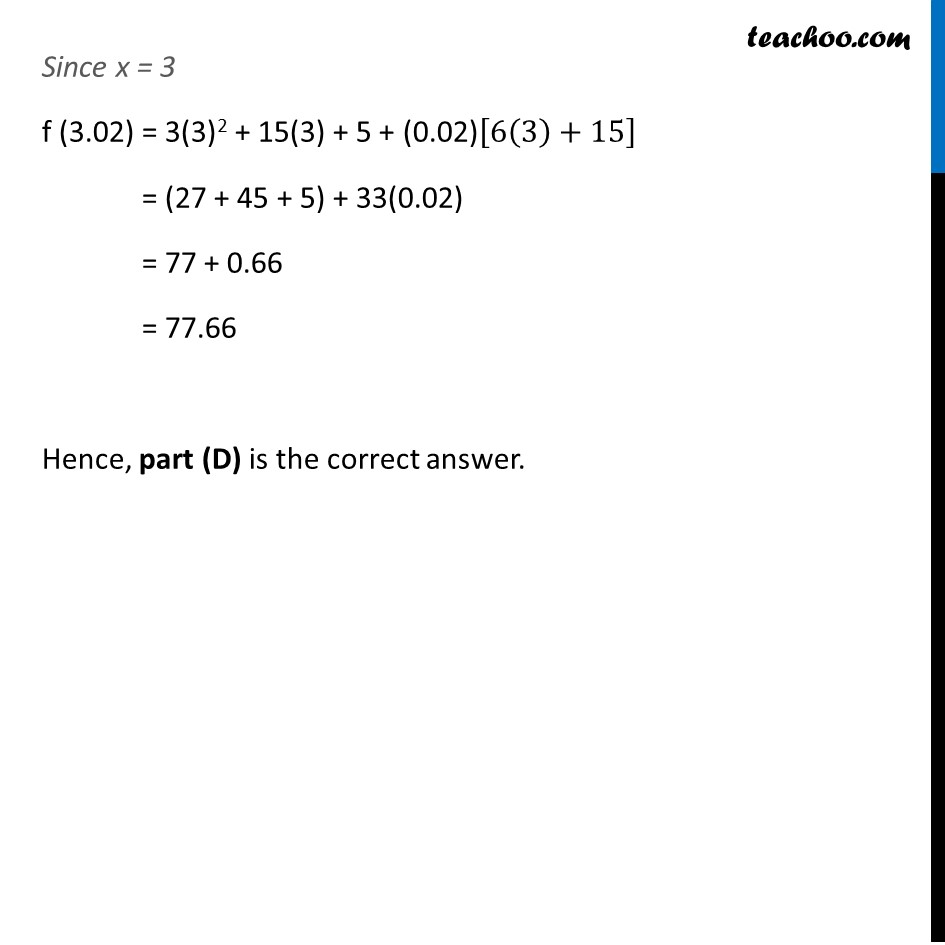
Question 8 If f(x) = 3x2 + 15x + 5, then the approximate value of f (3.02) is (A) 47.66 (B) 57.66 (C) 67.66 (D) 77.66Let x = 3 and ∆x = 0.02 f’(x) = 6x + 15 Now, ∆y = f’(x) ∆x = (6x + 15) 0.02 Also, ∆y = f (x + ∆x) − f(x) f (x + ∆x) = f (x) + ∆y f (3.02) = 3x2 + 15x + 5 + (6x + 15) (0.02) Since x = 3 f (3.02) = 3(3)2 + 15(3) + 5 + (0.02)[6(3)+15] = (27 + 45 + 5) + 33(0.02) = 77 + 0.66 = 77.66 Hence, part (D) is the correct answer.
