An empty cone of radius 3cm and height 12cm is filled with ice-cream

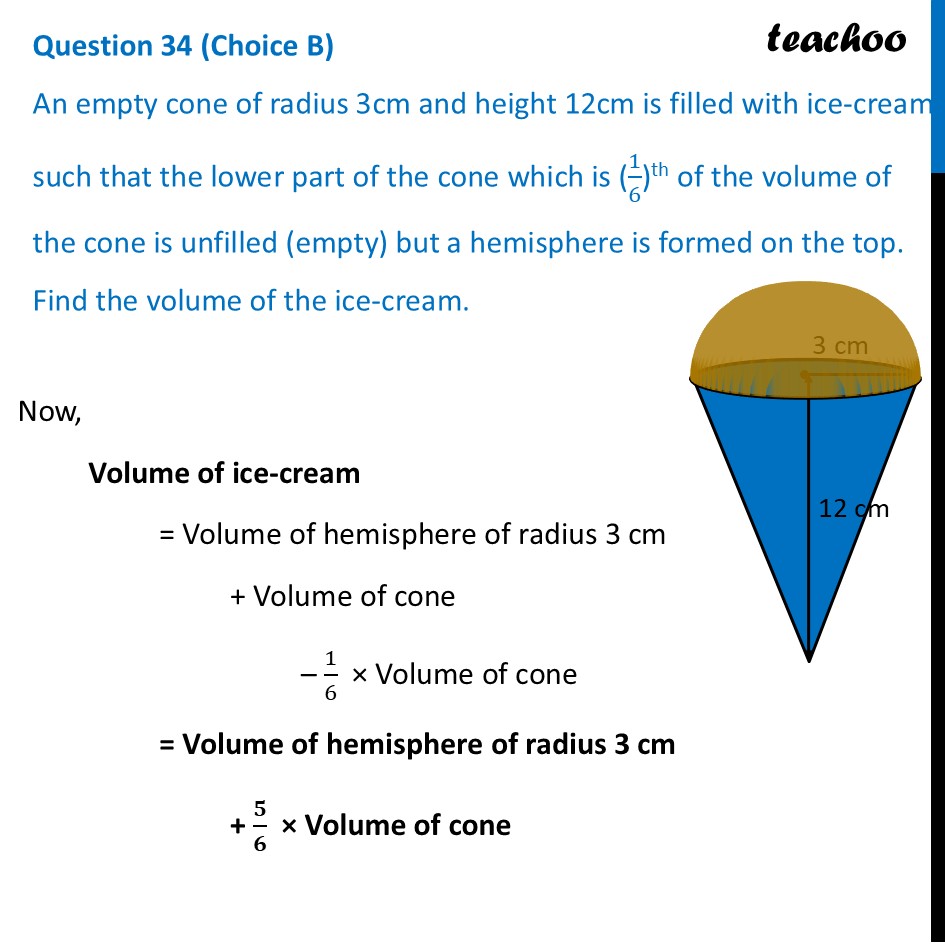
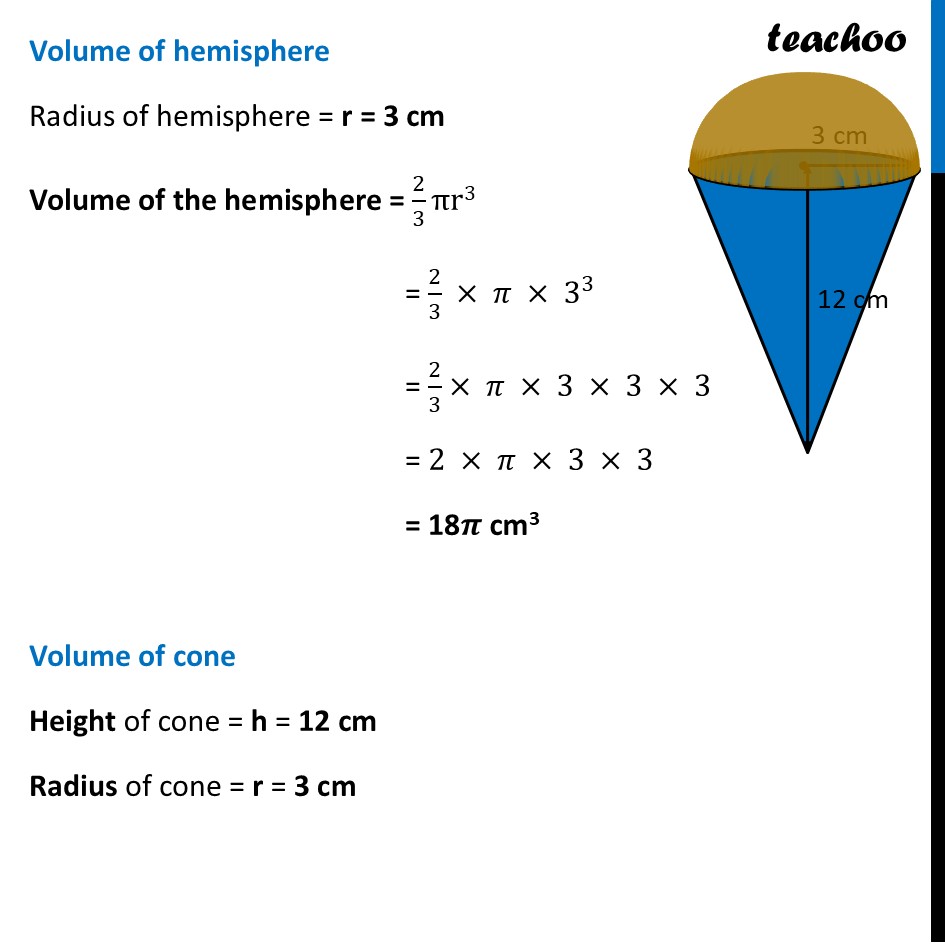
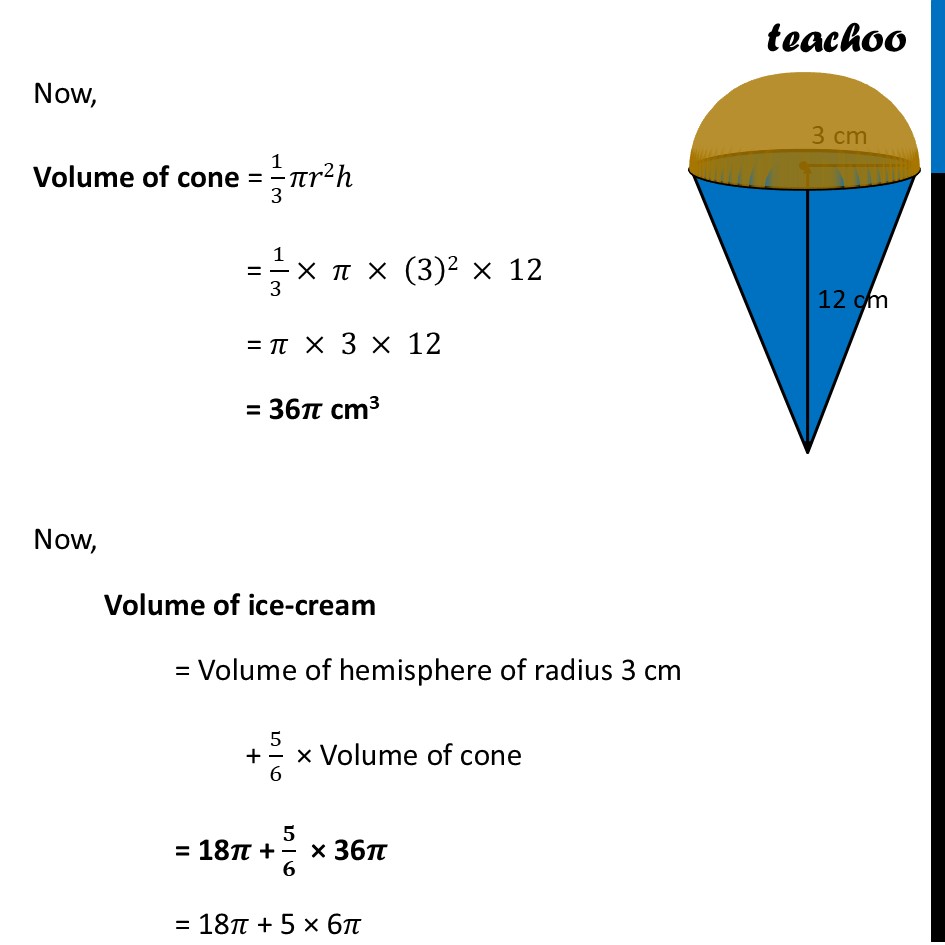
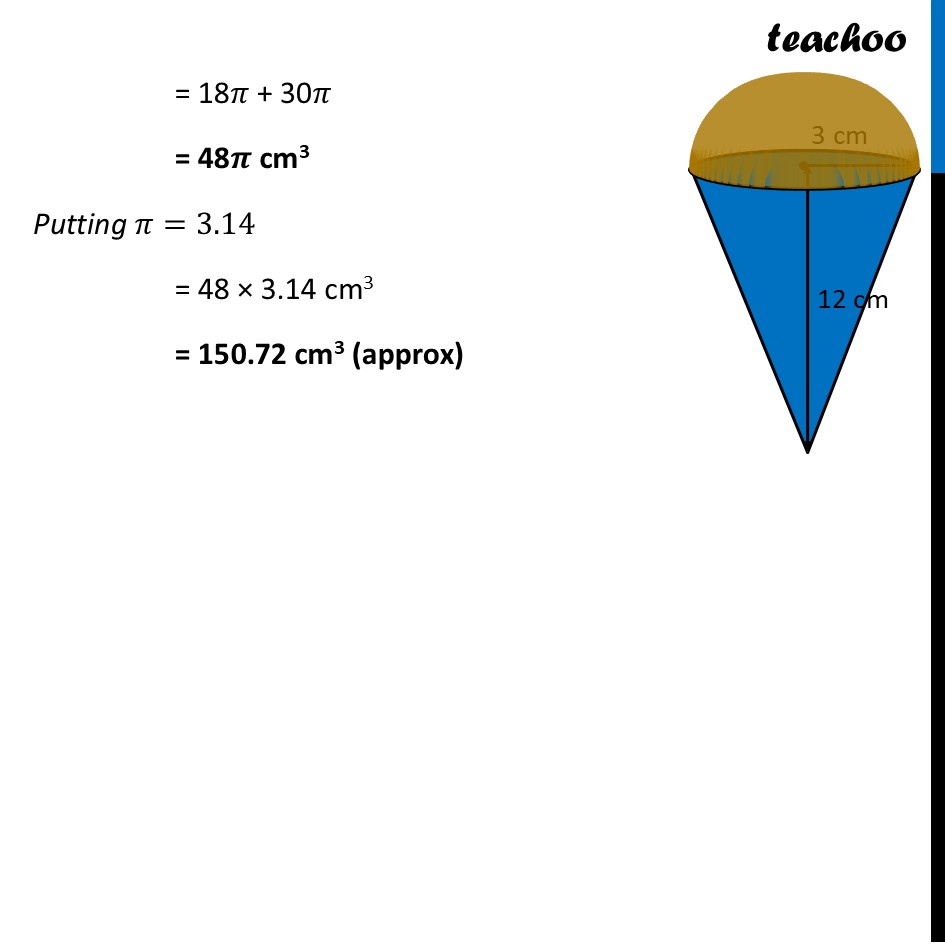
Question 34 (Choice B) An empty cone of radius 3cm and height 12cm is filled with ice-cream such that the lower part of the cone which is (1/6)th of the volume of the cone is unfilled (empty) but a hemisphere is formed on the top. Find the volume of the ice-cream.Now, Volume of ice-cream = Volume of hemisphere of radius 3 cm + Volume of cone – 1/6 × Volume of cone = Volume of hemisphere of radius 3 cm + 𝟓/𝟔 × Volume of cone Volume of hemisphere Radius of hemisphere = r = 3 cm Volume of the hemisphere = 2/3 πr3 = 2/3 × 𝜋 × 3^3 = 2/3× 𝜋 × 3 × 3 × 3 = 2 × 𝜋 × 3 × 3 = 18𝝅 cm3 Volume of cone Height of cone = h = 12 cm Radius of cone = r = 3 cm Now, Volume of cone = 1/3 𝜋𝑟2ℎ = 1/(3 )× 𝜋 × (3)2 × 12 = 𝜋 × 3 × 12 = 36𝝅 cm3 Now, Volume of ice-cream = Volume of hemisphere of radius 3 cm + 5/6 × Volume of cone = 18𝝅 + 𝟓/𝟔 × 36𝝅 = 18𝜋 + 5 × 6𝜋 = 18𝜋 + 30𝜋 = 48𝝅 cm3 Putting 𝜋=3.14 = 48 × 3.14 cm3 = 150.72 cm3 (approx)

Question 34 (B) - CBSE Class 10 Sample Paper for 2026 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Davneet Singh

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular