Question 33 - CBSE Class 10 Sample Paper for 2026 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Transcript

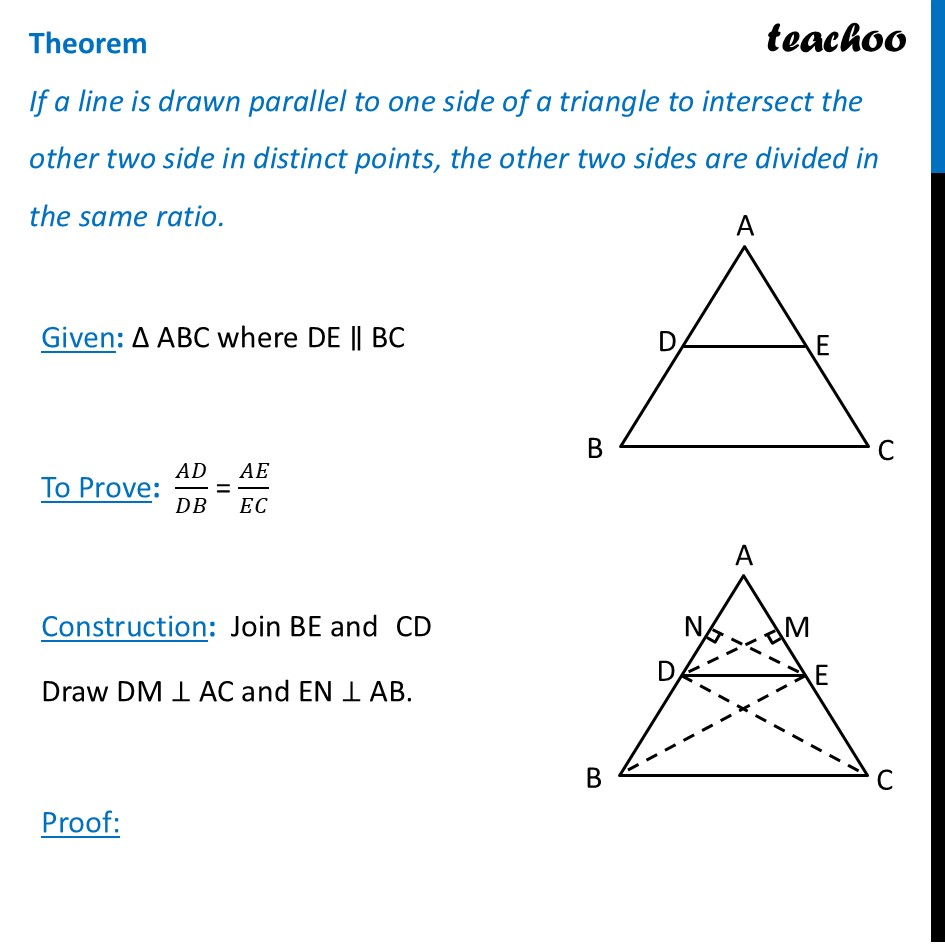
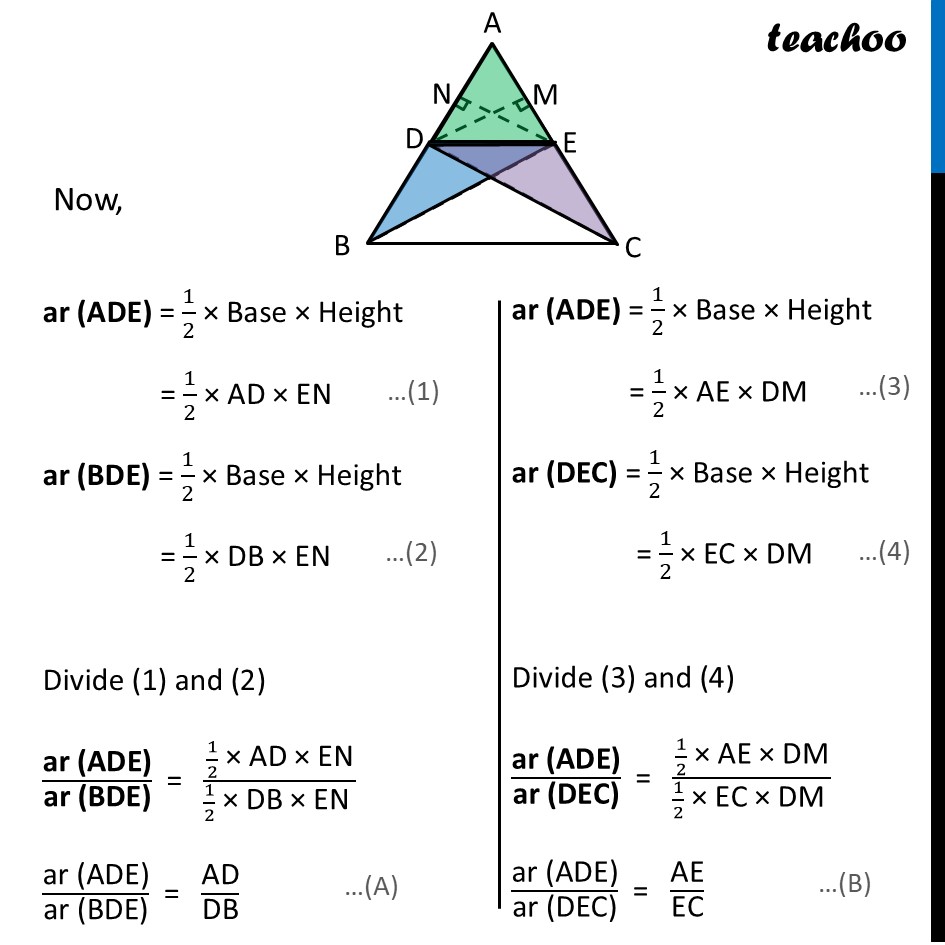
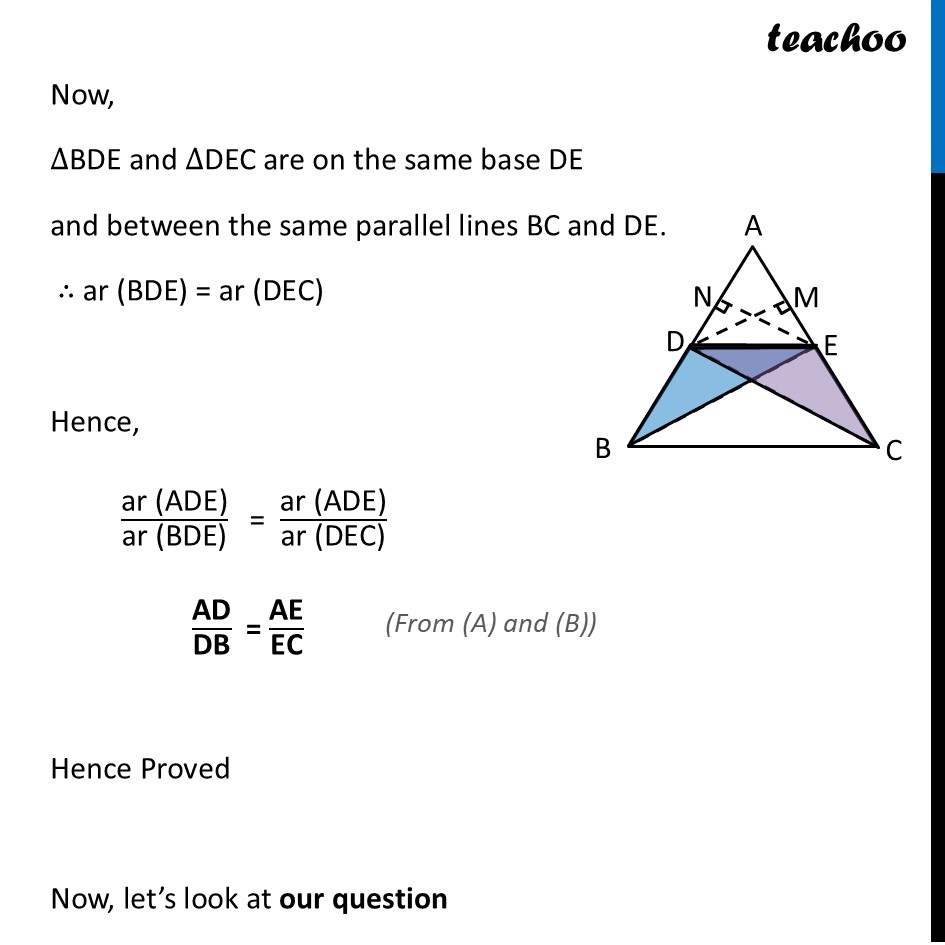
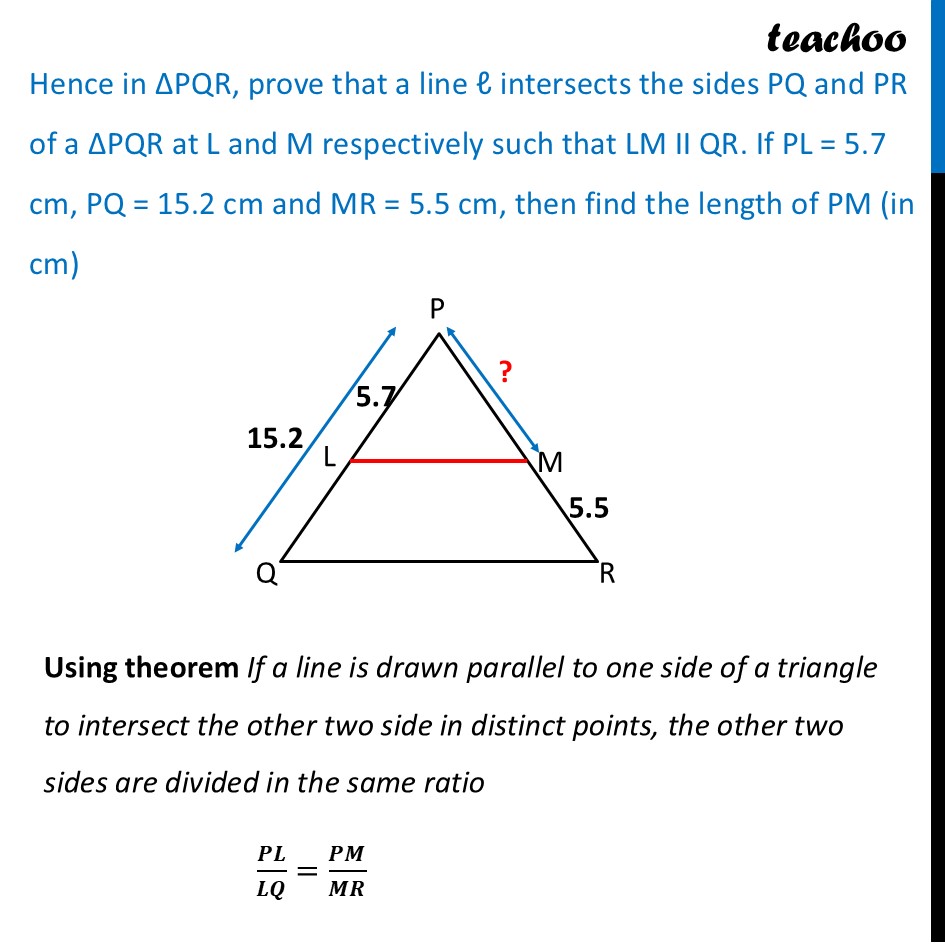
Question 33 Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio. Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non parallel sides in the same ratio.Let’s prove the theorem first Theorem If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio. Given: Δ ABC where DE ∥ BC To Prove: 𝐴𝐷/𝐷𝐵 = 𝐴𝐸/𝐸𝐶 Construction: Join BE and CD Draw DM ⊥ AC and EN ⊥ AB. Proof: Now, ar (ADE) = 1/2 × Base × Height = 1/2 × AD × EN ar (BDE) = 1/2 × Base × Height = 1/2 × DB × EN Divide (1) and (2) "ar (ADE)" /"ar (BDE)" = (1/2 " × AD × EN" )/(1/2 " × DB × EN " ) "ar (ADE)" /"ar (BDE)" = "AD" /"DB" ar (ADE) = 1/2 × Base × Height = 1/2 × AE × DM ar (DEC) = 1/2 × Base × Height = 1/2 × EC × DM Divide (3) and (4) "ar (ADE)" /"ar (DEC)" = (1/2 " × AE × DM" )/(1/2 " × EC × DM " ) "ar (ADE)" /"ar (DEC)" = "AE" /"EC" Now, ∆BDE and ∆DEC are on the same base DE and between the same parallel lines BC and DE. ∴ ar (BDE) = ar (DEC) Hence, "ar (ADE)" /"ar (BDE)" = "ar (ADE)" /"ar (DEC)" "AD" /"DB" = "AE" /"EC" Hence Proved Now, let’s look at our question Hence in ΔPQR, prove that a line ℓ intersects the sides PQ and PR of a ∆PQR at L and M respectively such that LM II QR. If PL = 5.7 cm, PQ = 15.2 cm and MR = 5.5 cm, then find the length of PM (in cm) Using theorem If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio 𝑷𝑳/𝑳𝑸=𝑷𝑴/𝑴𝑹 (𝟓.𝟕)/((𝟏𝟓.𝟐 − 𝟓.𝟕))=𝑷𝑴/(𝟓.𝟓) 5.7/9.5=𝑃𝑀/5.5 (57/10)/(95/10)=𝑃𝑀/5.5 57/95=𝑃𝑀/5.5 57/95 × 5.5=𝑃𝑀 57/95 ×55/10=𝑃𝑀 𝑃𝑀=57/19 ×11/10 𝑃𝑀=3 ×11/10 𝑃𝑀=33/10 𝑷𝑴=𝟑.𝟑 𝒄𝒎