


Examples
Example 2 Important
Example 3
Example 4 Important
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Important Deleted for CBSE Board 2024 Exams
Question 4 Important Deleted for CBSE Board 2024 Exams
Question 5 Important Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams
Question 8 Important Deleted for CBSE Board 2024 Exams
Question 9 Deleted for CBSE Board 2024 Exams
Question 10 Important Deleted for CBSE Board 2024 Exams You are here
Question 11 Important Deleted for CBSE Board 2024 Exams
Last updated at April 16, 2024 by Teachoo









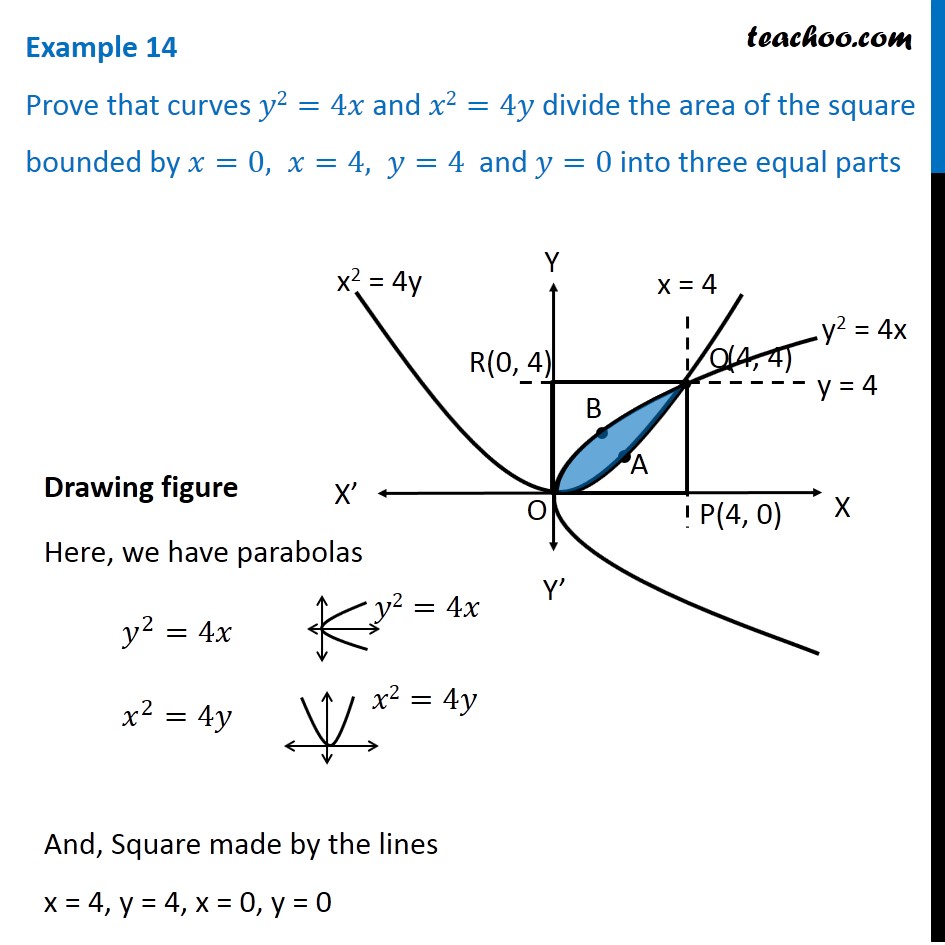
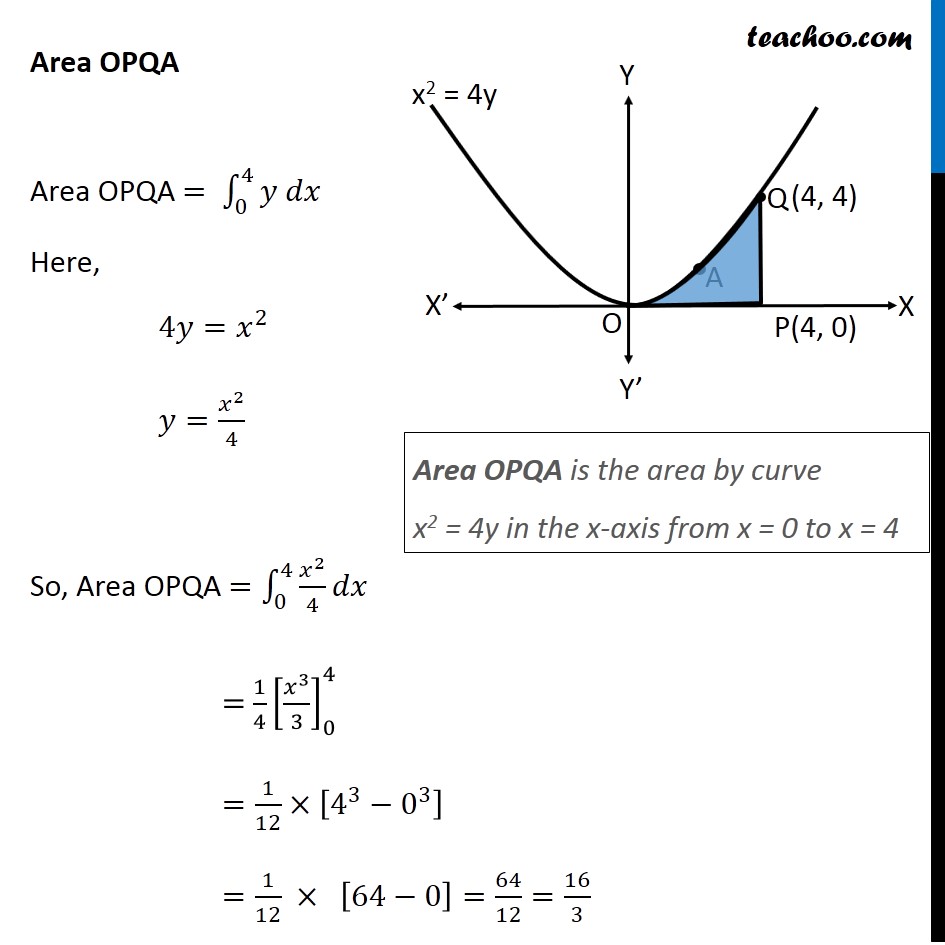
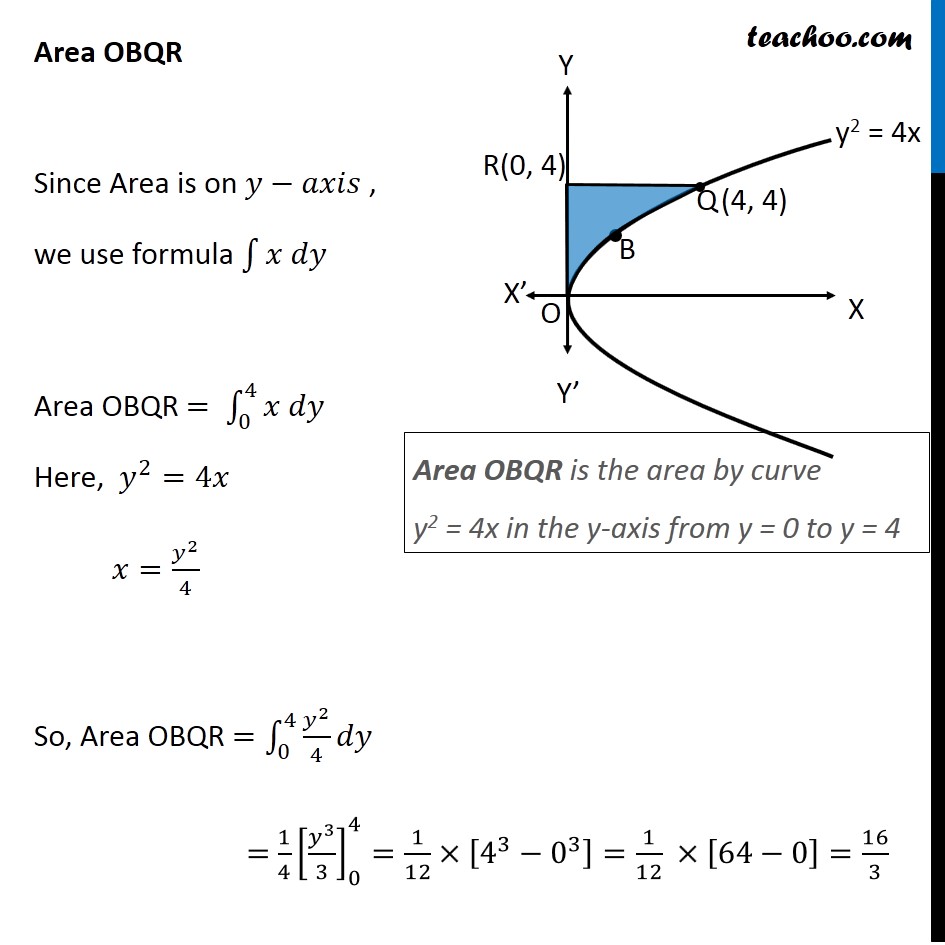
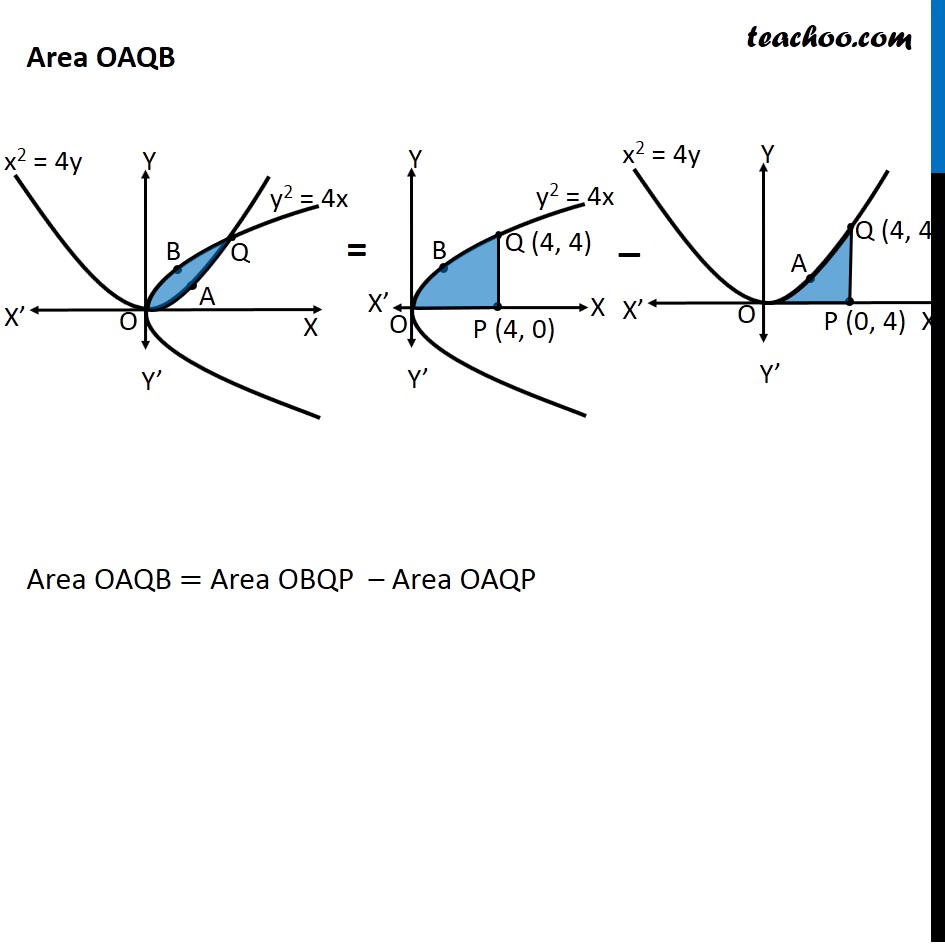
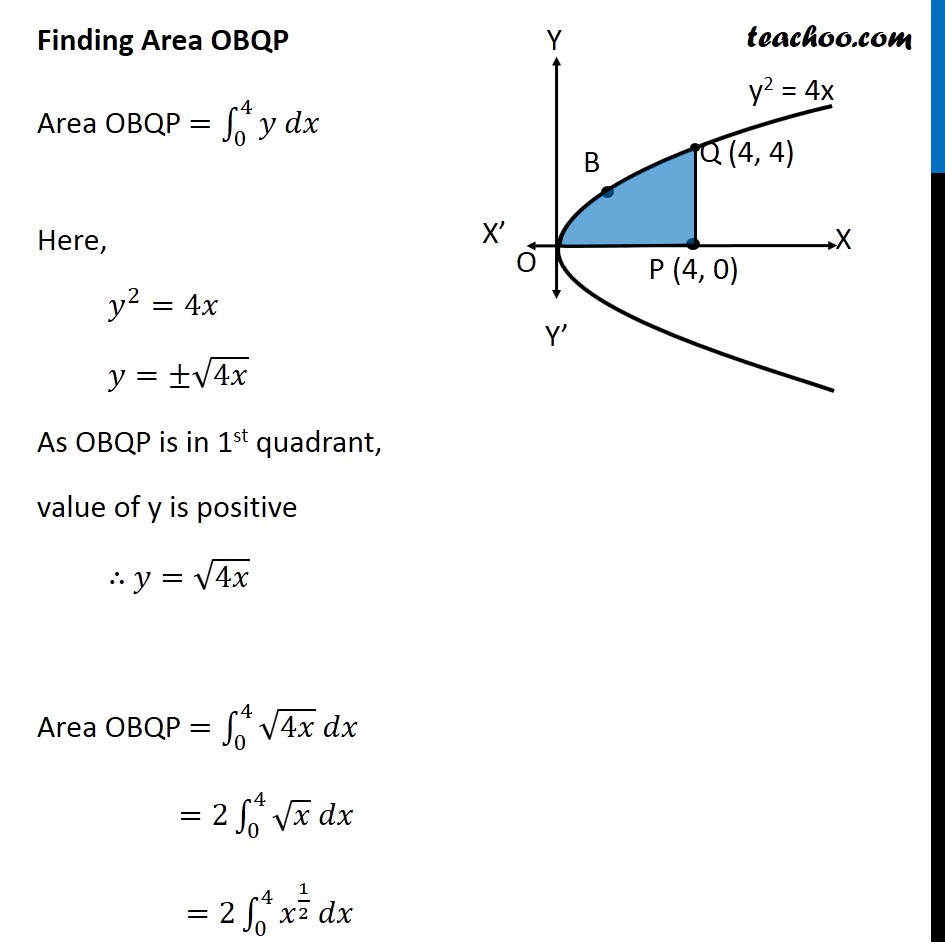
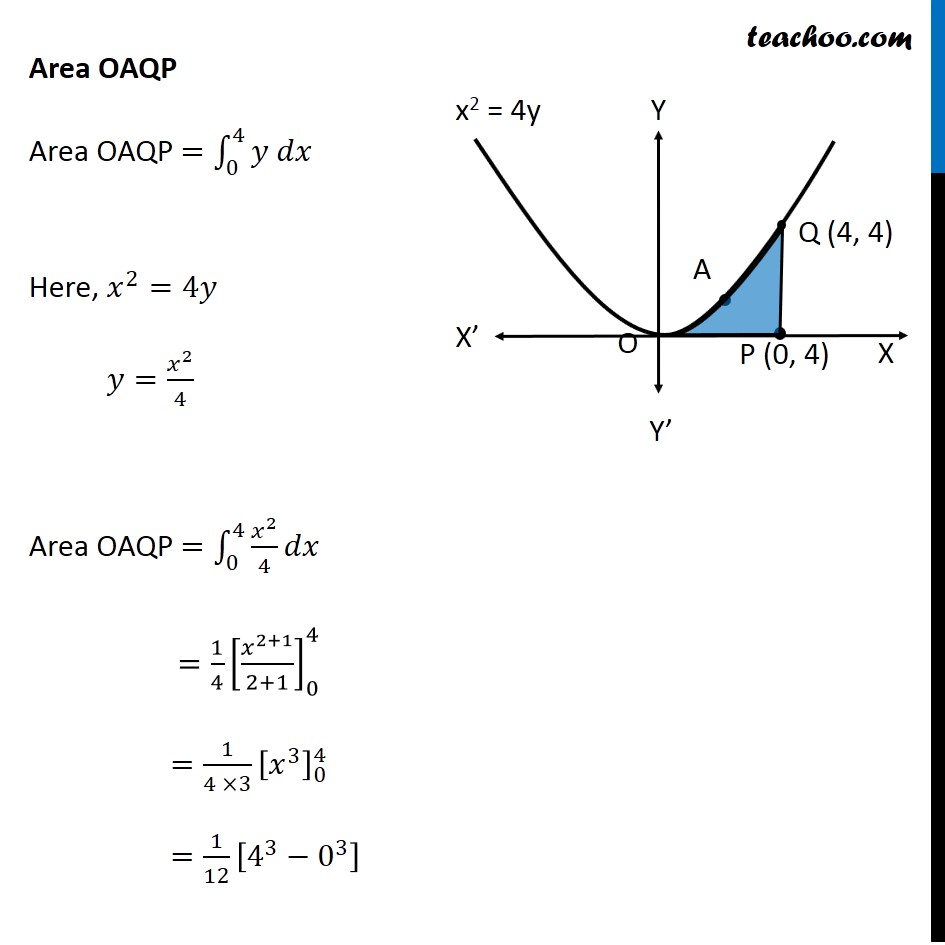
Question 10 Prove that curves 𝑦2=4𝑥 and 𝑥2=4𝑦 divide the area of the square bounded by 𝑥=0, 𝑥=4, 𝑦=4 and 𝑦=0 into three equal parts Drawing figure Here, we have parabolas 𝑦^2=4𝑥 𝑥^2=4𝑦 And, Square made by the lines x = 4, y = 4, x = 0, y = 0 We need to prove that area of square is divided into 3 parts by the curve So, we need to prove Area OPQA = Area OAQB = Area OBQR Area OPQA Area OPQA = ∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 4𝑦=𝑥^2 𝑦=𝑥^2/4 So, Area OPQA =∫_0^4▒〖𝑥^2/4 𝑑𝑥〗 = 1/4 [𝑥^3/3]_0^4 =1/12×[4^3−0^3 ] =1/12 × [64−0] =64/12=16/3 Area OPQA is the area by curve x2 = 4y in the x-axis from x = 0 to x = 4 Area OBQR Since Area is on 𝑦−𝑎𝑥𝑖𝑠 , we use formula ∫1▒〖𝑥 𝑑𝑦〗 Area OBQR = ∫_0^4▒〖𝑥 𝑑𝑦〗 Here, 𝑦^2=4𝑥 𝑥=𝑦^2/4 So, Area OBQR =∫_0^4▒〖𝑦^2/4 𝑑𝑦〗 = 1/4 [𝑦^3/3]_0^4=1/12×[4^3−0^3 ]=1/12 ×[64−0]=16/3 Area OBQR is the area by curve y2 = 4x in the y-axis from y = 0 to y = 4 Area OAQB Area OAQB = Area OBQP – Area OAQP Finding Area OBQP Area OBQP =∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 𝑦^2=4𝑥 𝑦=±√4𝑥 As OBQP is in 1st quadrant, value of y is positive ∴ 𝑦=√4𝑥 Area OBQP =∫_0^4▒〖√4𝑥 𝑑𝑥〗 =2∫_0^4▒〖√𝑥 𝑑𝑥〗 =2∫_0^4▒〖𝑥^(1/2) 𝑑𝑥〗 =2 × [𝑥^(1/2+1)/(1/2+1)]_0^4 =2 × [𝑥^(3/2)/(3/2)]_0^4 =2 × 2/3 [𝑥^(3/2) ]_0^4 =4/3 [(4)^(3/2)−(0)^(3/2) ] =4/3 [8−0] =32/3 Area OAQP Area OAQP =∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 𝑥^2=4𝑦 𝑦=𝑥^2/4 Area OAQP =∫_0^4▒〖𝑥^2/4 𝑑𝑥〗 =1/4 [𝑥^(2+1)/(2+1)]_0^4 =1/(4 ×3) [𝑥^3 ]_0^4 =1/12 [4^3−0^3 ] Area OAQP Area OAQP =∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 𝑥^2=4𝑦 𝑦=𝑥^2/4 Area OAQP =∫_0^4▒〖𝑥^2/4 𝑑𝑥〗 =1/4 [𝑥^(2+1)/(2+1)]_0^4 =1/(4 ×3) [𝑥^3 ]_0^4 =1/12 [4^3−0^3 ] =1/12 × [64−0] =16/3 ∴ Area OAQB = Area OBQD – Area OAQP = 32/3−16/3 = 16/3 So, Area OAQB = Area OAQP = Area OBRQ = 𝟏𝟔/𝟑 square units Hence Proved.