Question 7 - Examples - Chapter 8 Class 12 Application of Integrals

Transcript

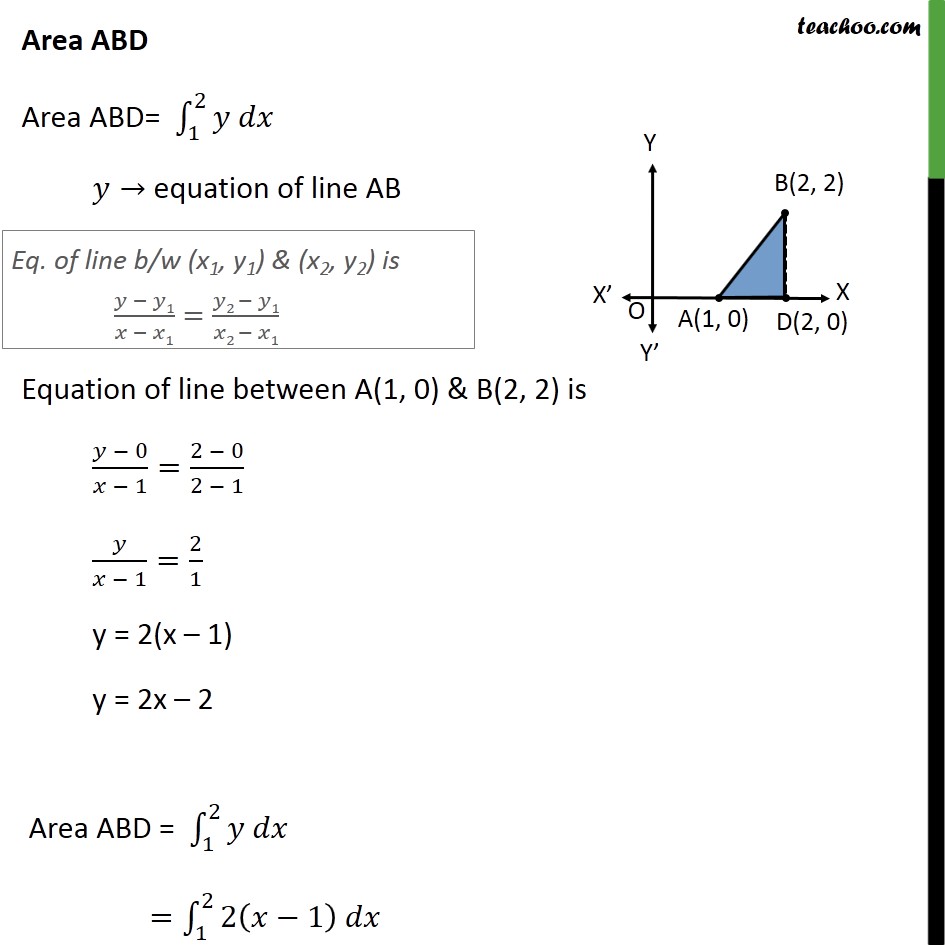
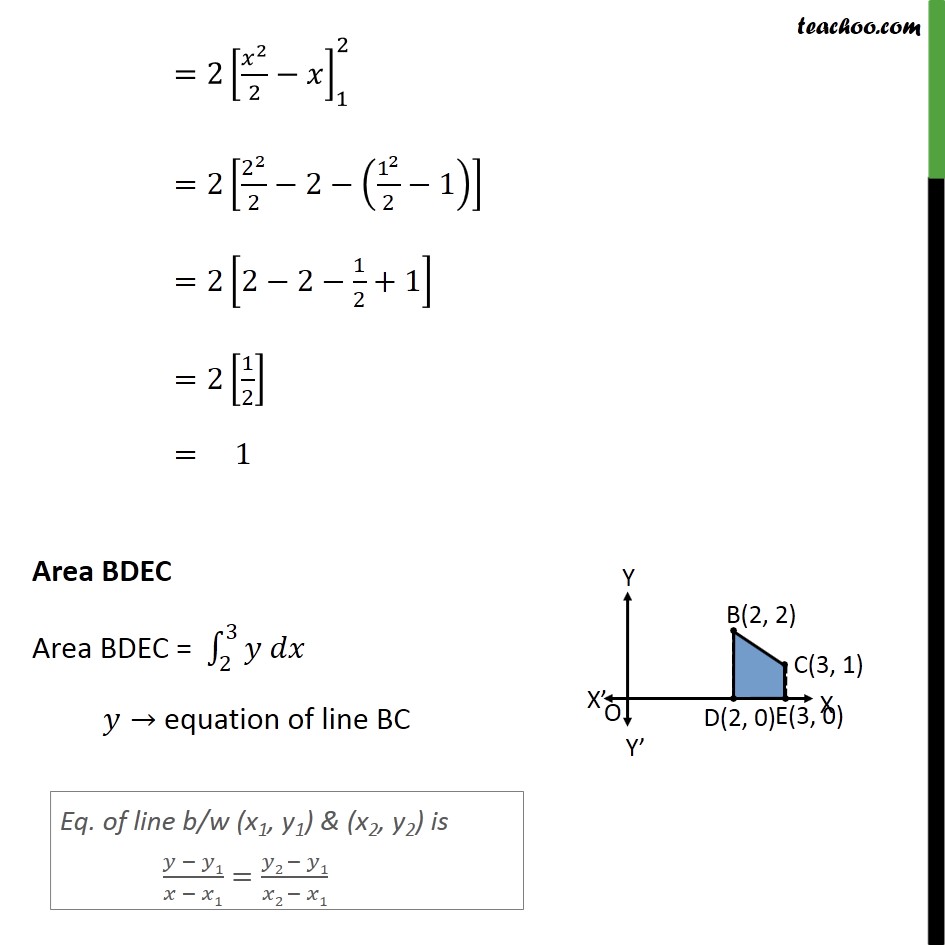
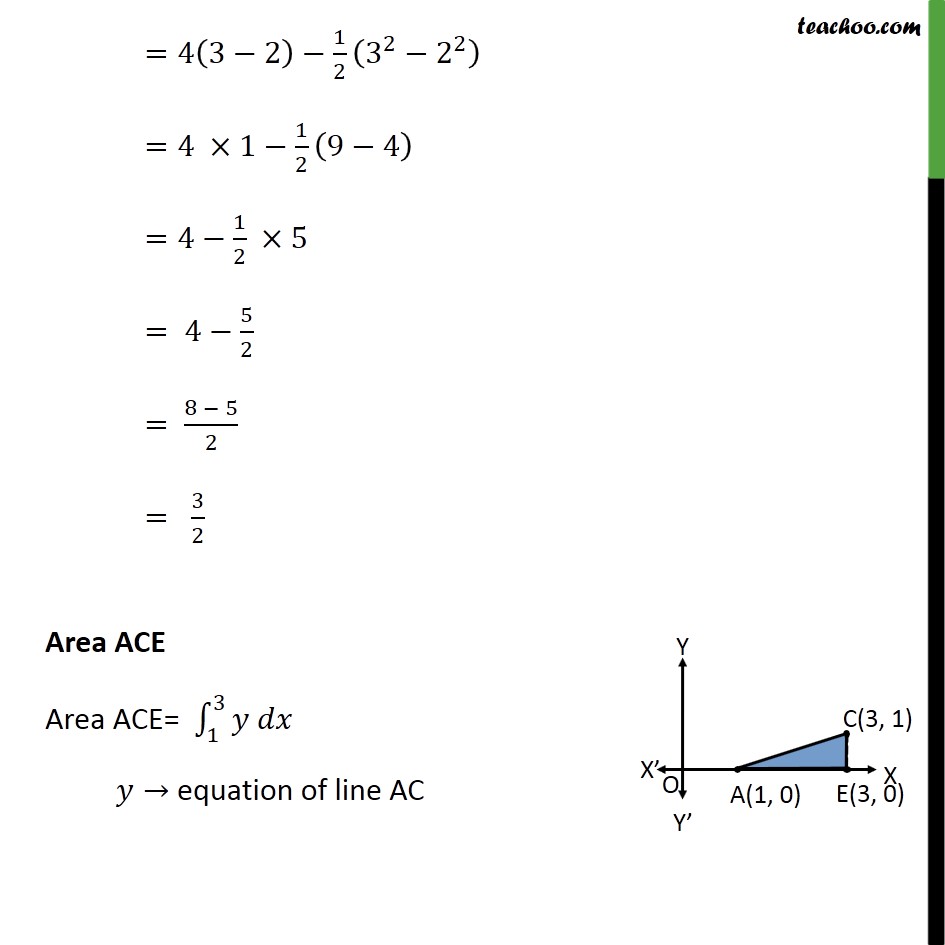
Question 7 Using integration find the area of region bounded by the triangle whose vertices are (1, 0), (2, 2) and (3, 1) Area of ∆ formed by point 1 , 0﷯ , 2 ,2﷯ & 3 , 1﷯ Step 1: Draw the figure Area ABD Area ABD= 1﷮2﷮𝑦 𝑑𝑥﷯ 𝑦→ equation of line AB Equation of line between A(1, 0) & B(2, 2) is 𝑦 − 0﷮𝑥 − 1﷯= 2 − 0﷮2 − 1﷯ 𝑦﷮𝑥 − 1﷯= 2﷮1﷯ y = 2(x – 1) y = 2x – 2 Area ABD = 1﷮2﷮𝑦 𝑑𝑥﷯ = 1﷮2﷮2 𝑥−1﷯ 𝑑𝑥﷯ = 2 𝑥﷮2﷯﷮2﷯−𝑥﷯﷮1﷮2﷯ =2 2﷮2﷯﷮2﷯−2− 1﷮2﷯﷮2﷯−1﷯﷯ =2 2−2− 1﷮2﷯+1﷯ =2 1﷮2﷯﷯ = 1 Area BDEC Area BDEC = 2﷮3﷮𝑦 𝑑𝑥﷯ 𝑦→ equation of line BC Equation of line between B(2, 2) & C(3, 1) is 𝑦 − 2﷮𝑥 − 2﷯= 1 − 2﷮3 − 2﷯ 𝑦 − 2﷮𝑥 − 2﷯= −1﷮1﷯ y – 2 = –1(x – 2) y – 2 = –x + 2 y = 4 – x Area BDEC = 2﷮3﷮𝑦 𝑑𝑥﷯ = 2﷮3﷮ 4−𝑥﷯﷯ 𝑑𝑥 =4 2﷮3﷮𝑑𝑥−﷯ 2﷮3﷮𝑥𝑑𝑥﷯ =4 𝑥﷯﷮2﷮3﷯− 𝑥﷮2﷯﷮2﷯﷯﷮2﷮3﷯ =4 3−2﷯− 1﷮2﷯ 3﷮2﷯− 2﷮2﷯﷯ =4 ×1− 1﷮2﷯ 9−4﷯ =4− 1﷮2﷯ ×5 = 4− 5﷮2﷯ = 8 − 5﷮2﷯ = 3﷮2﷯ Area ACE Area ACE= 1﷮3﷮𝑦 𝑑𝑥﷯ 𝑦→ equation of line AC Equation of line between A(1, 0) & C(3, 1) is 𝑦 − 0﷮𝑥 − 1﷯= 1 − 0﷮3 − 1﷯ 𝑦﷮𝑥 − 1﷯= 1﷮2﷯ y = 1﷮2﷯ (x – 1) Area ACE = 1﷮3﷮𝑦 𝑑𝑥﷯ = 1﷮3﷮ 1﷮2﷯ 𝑥−1﷯ 𝑑𝑥﷯ = 1﷮2﷯ 1﷮3﷮ 𝑥−1﷯ 𝑑𝑥﷯ = 1﷮2﷯ 𝑥﷮2﷯﷮2﷯−𝑥﷯﷮1﷮3﷯ = 1﷮2﷯ 3﷮2﷯﷮2﷯−3− 1﷮2﷯﷮2﷯−1﷯﷯ = 1﷮2﷯ 9﷮2﷯−3− 1﷮2﷯+1﷯ = 1﷮2﷯ 4﷮2﷯﷯ =1 Hence Area Required = Area ABD + Area BDEC – Area ACE = 1 + 3﷮2﷯−1 = 3﷮2﷯