Example 12 - Chapter 8 Class 12 Application of Integrals (Term 2)
Last updated at May 29, 2018 by Teachoo
Examples
Example 1
Example 2 Important
Example 3
Example 4
Example 5 Important
Example 6 Important Deleted for CBSE Board 2022 Exams
Example 7 Important Deleted for CBSE Board 2022 Exams
Example 8 Important Deleted for CBSE Board 2022 Exams
Example 9 Deleted for CBSE Board 2022 Exams
Example 10 Important Deleted for CBSE Board 2022 Exams
Example 11
Example 12 You are here
Example 13 Important
Example 14 Important Deleted for CBSE Board 2022 Exams
Example 15 Important
Chapter 8 Class 12 Application of Integrals (Term 2)
Serial order wise
Transcript
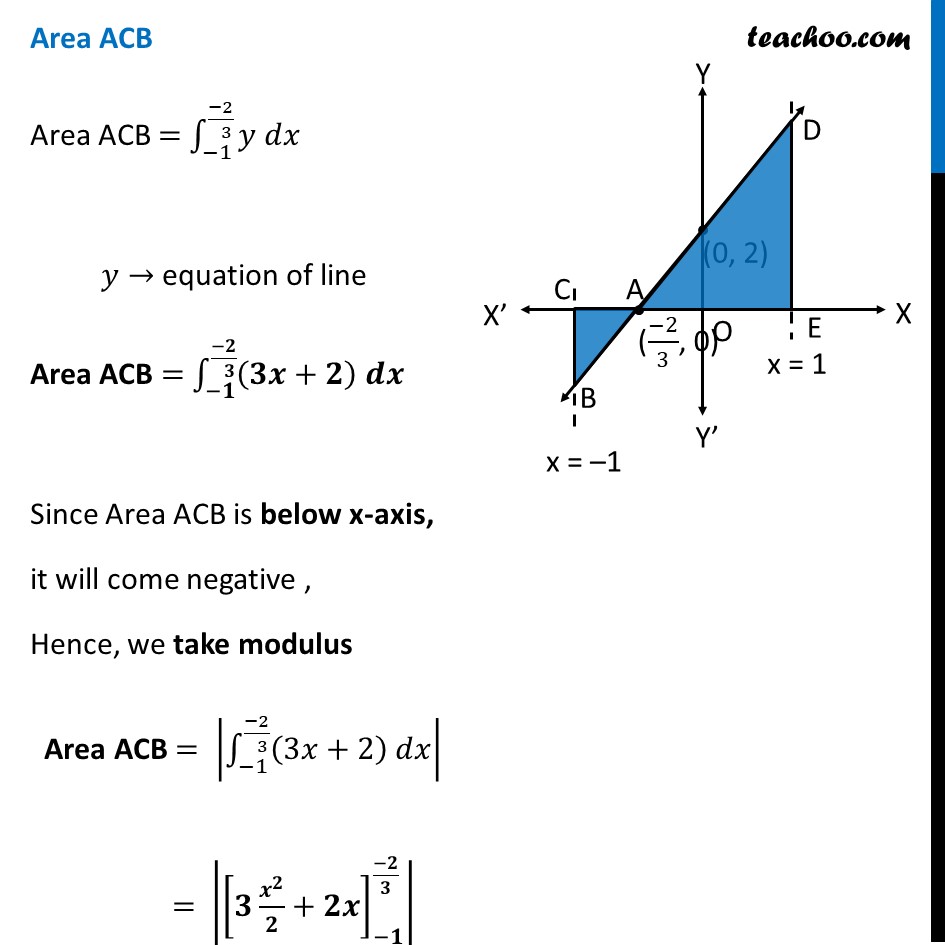
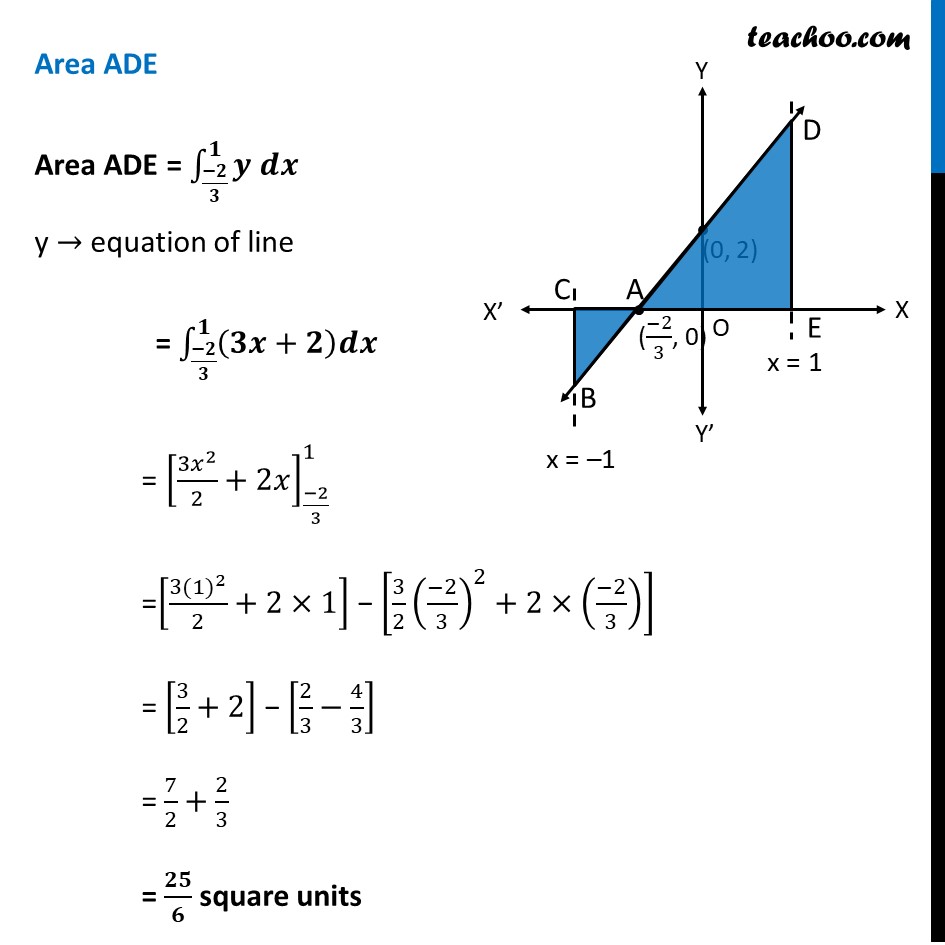
Example 12 Find the area of region bounded by the line =3 +2, the and the ordinates = 1 and =1 First Plotting =3 +2 In graph Area Required = Area ACB + Area ADE Area ACB Area ACB = 1 2 3 equation of line Area ACB = 1 2 3 3 +2 Since Area ACB is below x-axis, it will come negative , Hence, we take modulus Area ACB = 1 2 3 3 +2 = 3 2 2 +2 1 2 3 = 3 2 2 3 2 +2 2 3 3 2 1 2 +2( 1) = 3 2 4 9 4 3 3 2 2 = 2 3 1 2 = 2 3 + 1 2 = 1 6 = 1 6 Area ADE Area ADE = 2 3 1 y equation of line = 2 3 1 3 +2 = 3 2 2 +2 2 3 1 = 3 (1) 2 2 +2 1 3 2 2 3 2 +2 2 3 = 3 2 +2 2 3 4 3 = 7 2 + 2 3 = 25 6 Thus, Required Area = Area ACB + Area ADE = 1 6 + 25 6 = 26 6 = 13 3
