Question 10 - Examples - Chapter 8 Class 12 Application of Integrals

Transcript

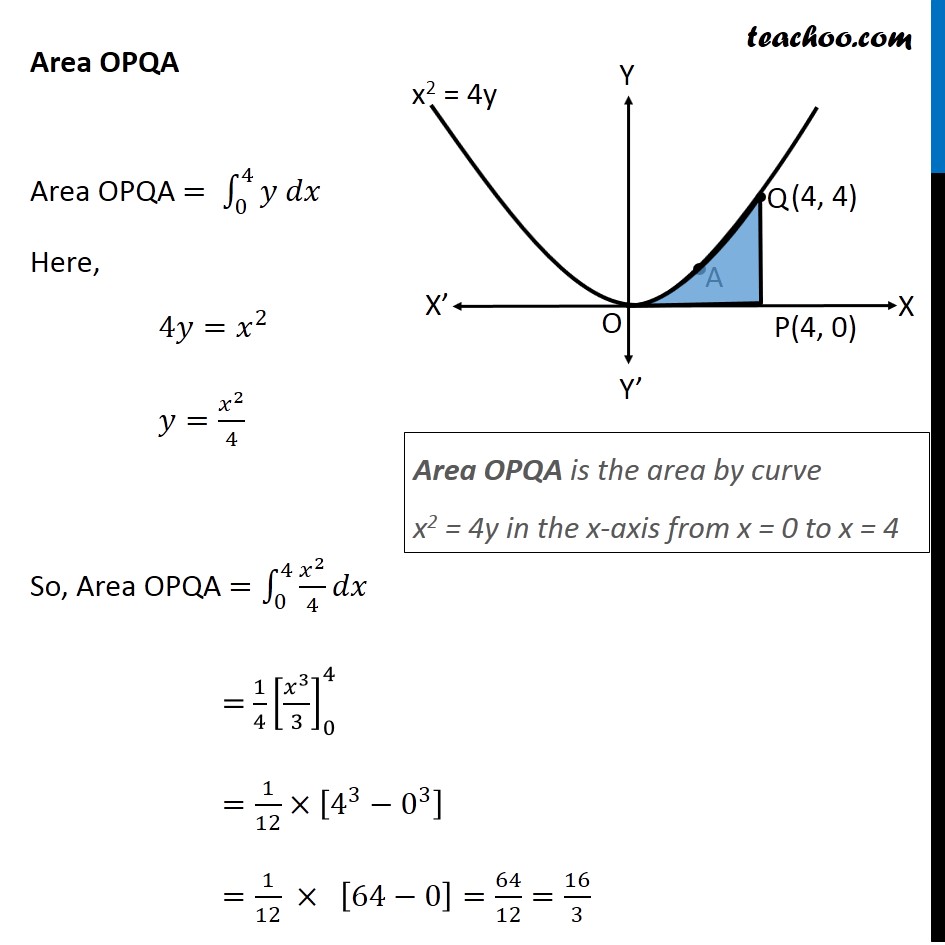
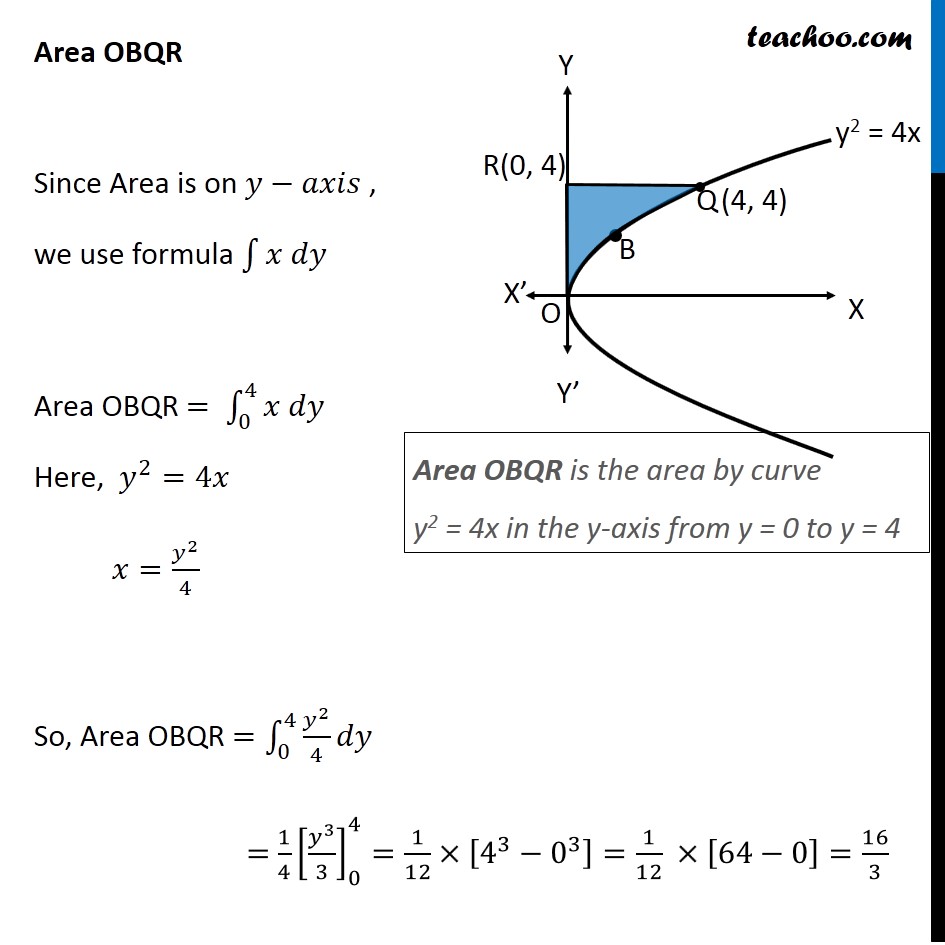
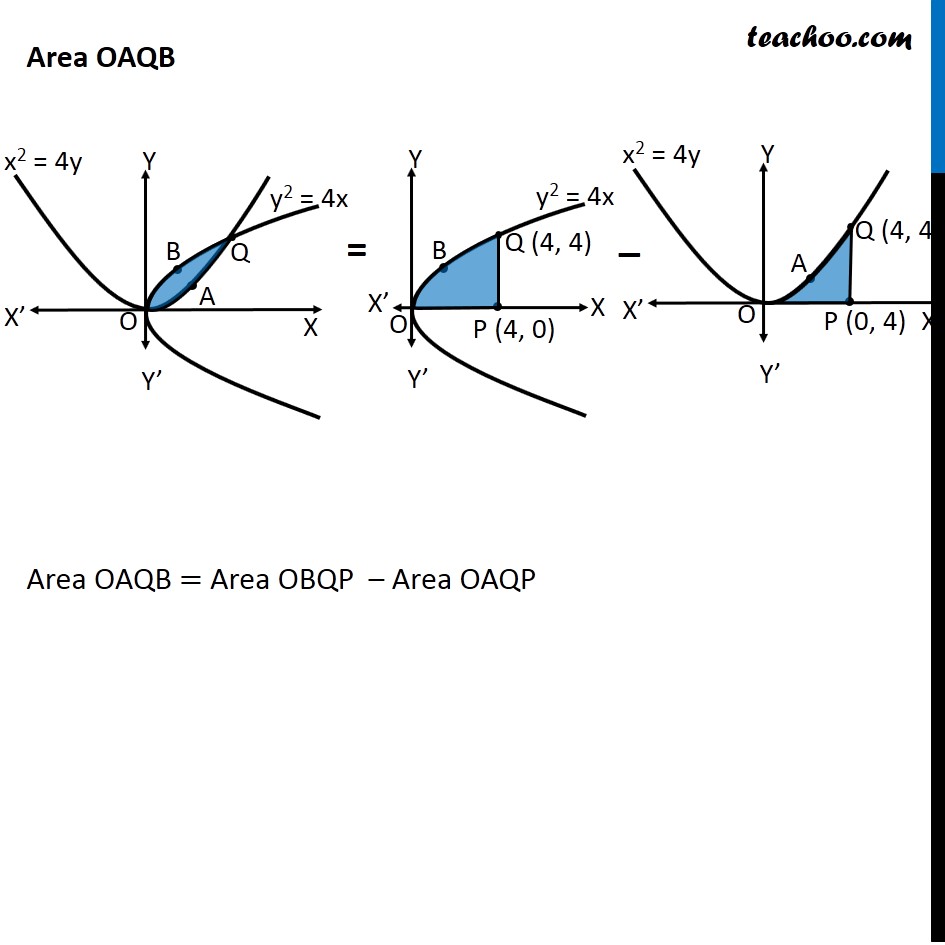
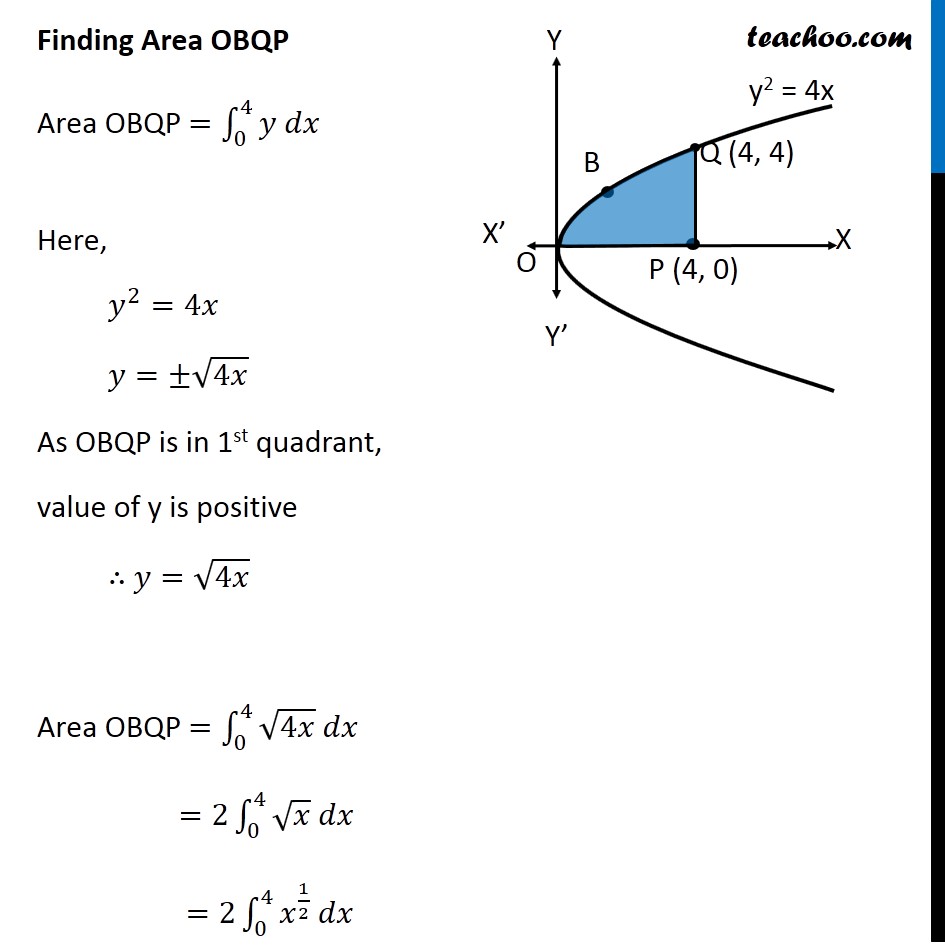
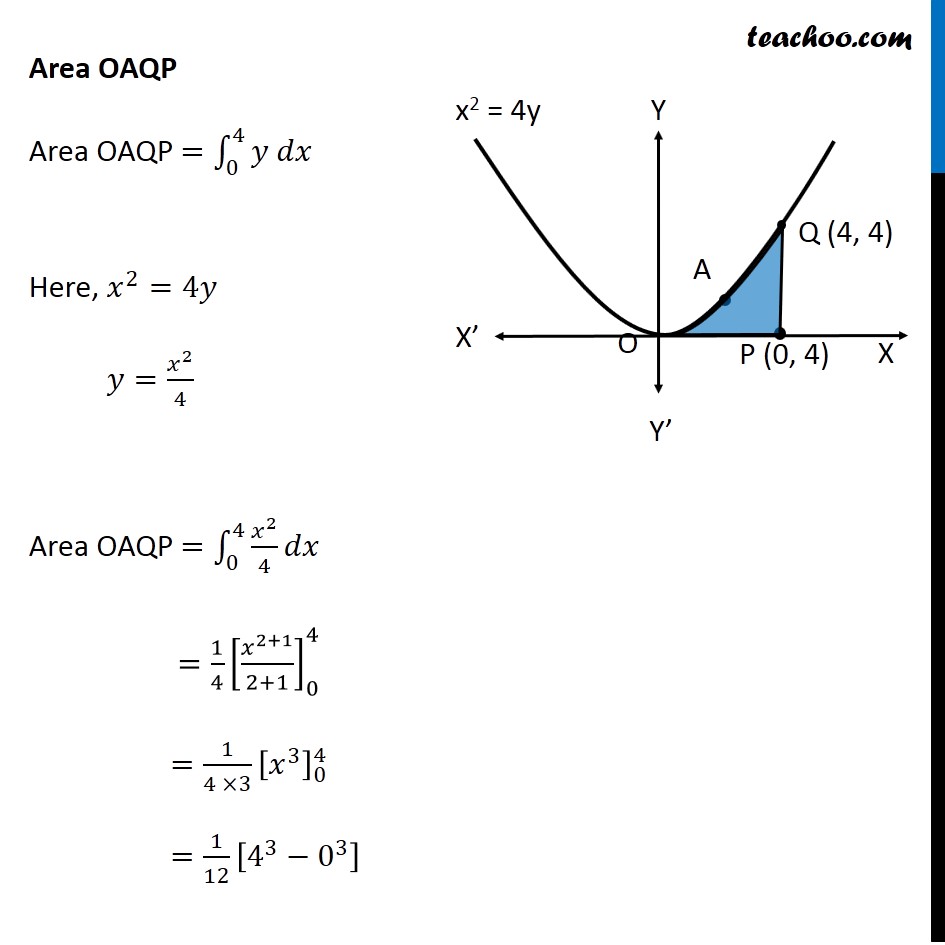
Question 10 Prove that curves 𝑦2=4𝑥 and 𝑥2=4𝑦 divide the area of the square bounded by 𝑥=0, 𝑥=4, 𝑦=4 and 𝑦=0 into three equal parts Drawing figure Here, we have parabolas 𝑦^2=4𝑥 𝑥^2=4𝑦 And, Square made by the lines x = 4, y = 4, x = 0, y = 0 We need to prove that area of square is divided into 3 parts by the curve So, we need to prove Area OPQA = Area OAQB = Area OBQR Area OPQA Area OPQA = ∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 4𝑦=𝑥^2 𝑦=𝑥^2/4 So, Area OPQA =∫_0^4▒〖𝑥^2/4 𝑑𝑥〗 = 1/4 [𝑥^3/3]_0^4 =1/12×[4^3−0^3 ] =1/12 × [64−0] =64/12=16/3 Area OPQA is the area by curve x2 = 4y in the x-axis from x = 0 to x = 4 Area OBQR Since Area is on 𝑦−𝑎𝑥𝑖𝑠 , we use formula ∫1▒〖𝑥 𝑑𝑦〗 Area OBQR = ∫_0^4▒〖𝑥 𝑑𝑦〗 Here, 𝑦^2=4𝑥 𝑥=𝑦^2/4 So, Area OBQR =∫_0^4▒〖𝑦^2/4 𝑑𝑦〗 = 1/4 [𝑦^3/3]_0^4=1/12×[4^3−0^3 ]=1/12 ×[64−0]=16/3 Area OBQR is the area by curve y2 = 4x in the y-axis from y = 0 to y = 4 Area OAQB Area OAQB = Area OBQP – Area OAQP Finding Area OBQP Area OBQP =∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 𝑦^2=4𝑥 𝑦=±√4𝑥 As OBQP is in 1st quadrant, value of y is positive ∴ 𝑦=√4𝑥 Area OBQP =∫_0^4▒〖√4𝑥 𝑑𝑥〗 =2∫_0^4▒〖√𝑥 𝑑𝑥〗 =2∫_0^4▒〖𝑥^(1/2) 𝑑𝑥〗 =2 × [𝑥^(1/2+1)/(1/2+1)]_0^4 =2 × [𝑥^(3/2)/(3/2)]_0^4 =2 × 2/3 [𝑥^(3/2) ]_0^4 =4/3 [(4)^(3/2)−(0)^(3/2) ] =4/3 [8−0] =32/3 Area OAQP Area OAQP =∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 𝑥^2=4𝑦 𝑦=𝑥^2/4 Area OAQP =∫_0^4▒〖𝑥^2/4 𝑑𝑥〗 =1/4 [𝑥^(2+1)/(2+1)]_0^4 =1/(4 ×3) [𝑥^3 ]_0^4 =1/12 [4^3−0^3 ] Area OAQP Area OAQP =∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 𝑥^2=4𝑦 𝑦=𝑥^2/4 Area OAQP =∫_0^4▒〖𝑥^2/4 𝑑𝑥〗 =1/4 [𝑥^(2+1)/(2+1)]_0^4 =1/(4 ×3) [𝑥^3 ]_0^4 =1/12 [4^3−0^3 ] =1/12 × [64−0] =16/3 ∴ Area OAQB = Area OBQD – Area OAQP = 32/3−16/3 = 16/3 So, Area OAQB = Area OAQP = Area OBRQ = 𝟏𝟔/𝟑 square units Hence Proved.