Question 4 - Examples - Chapter 8 Class 12 Application of Integrals

Transcript

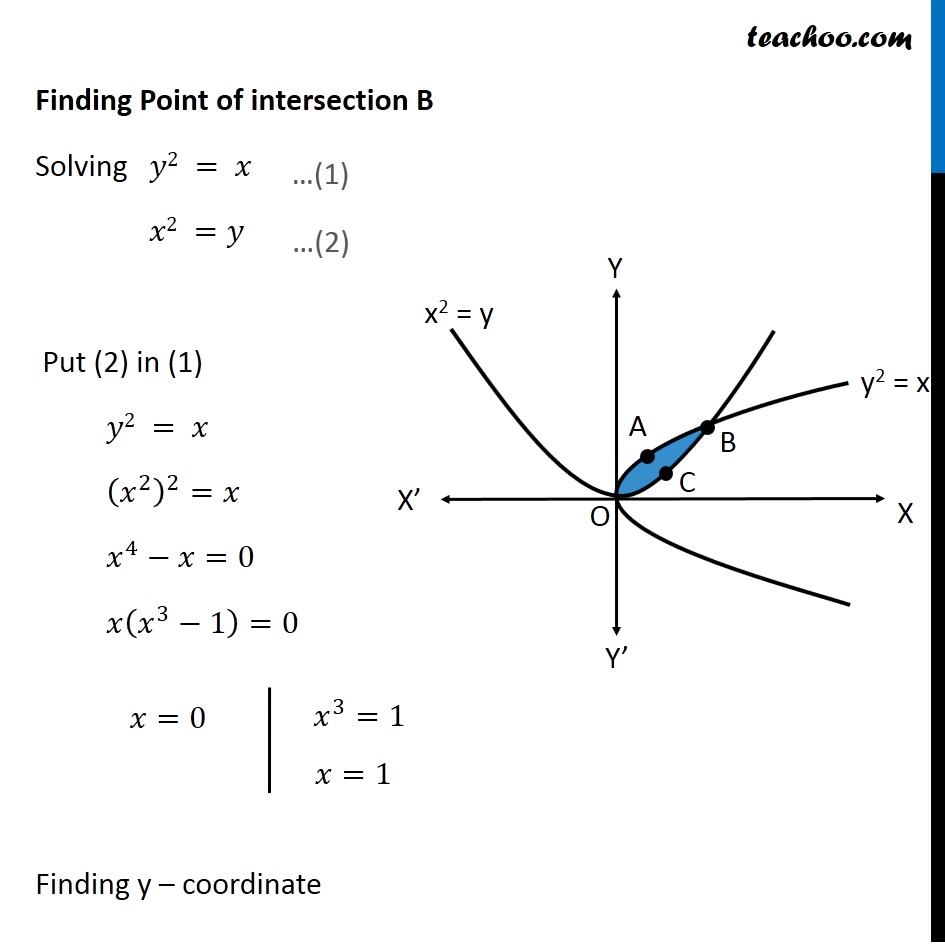
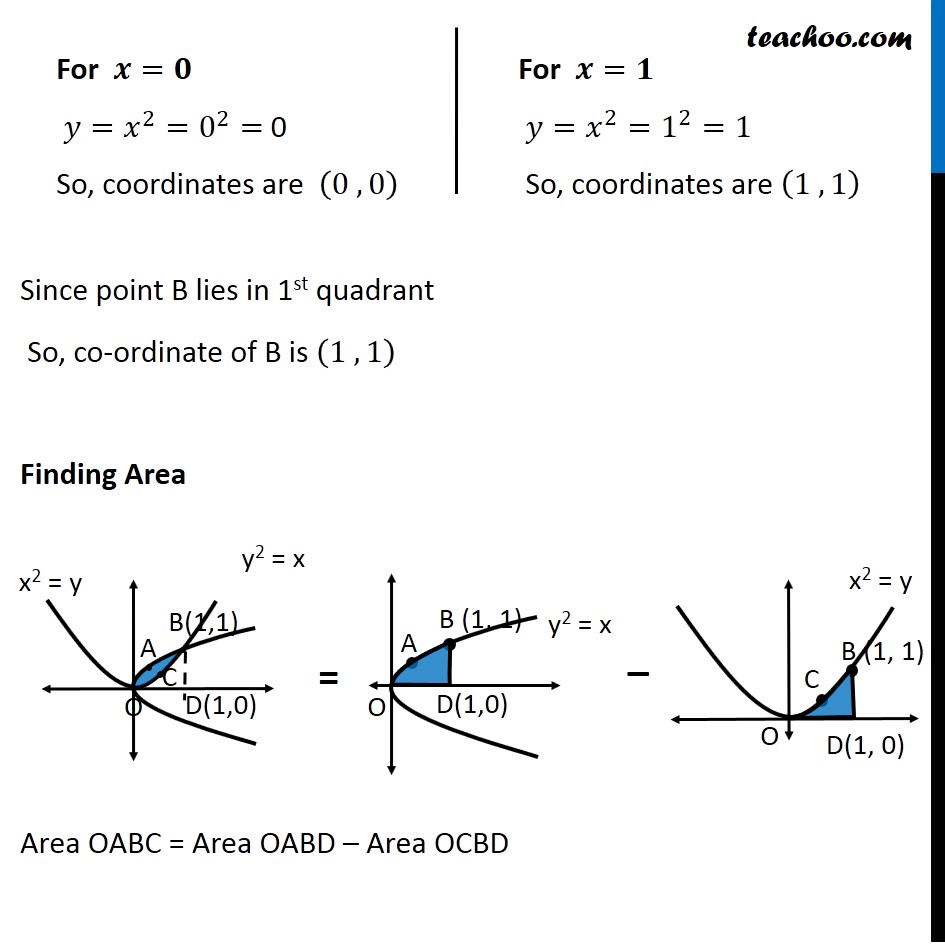
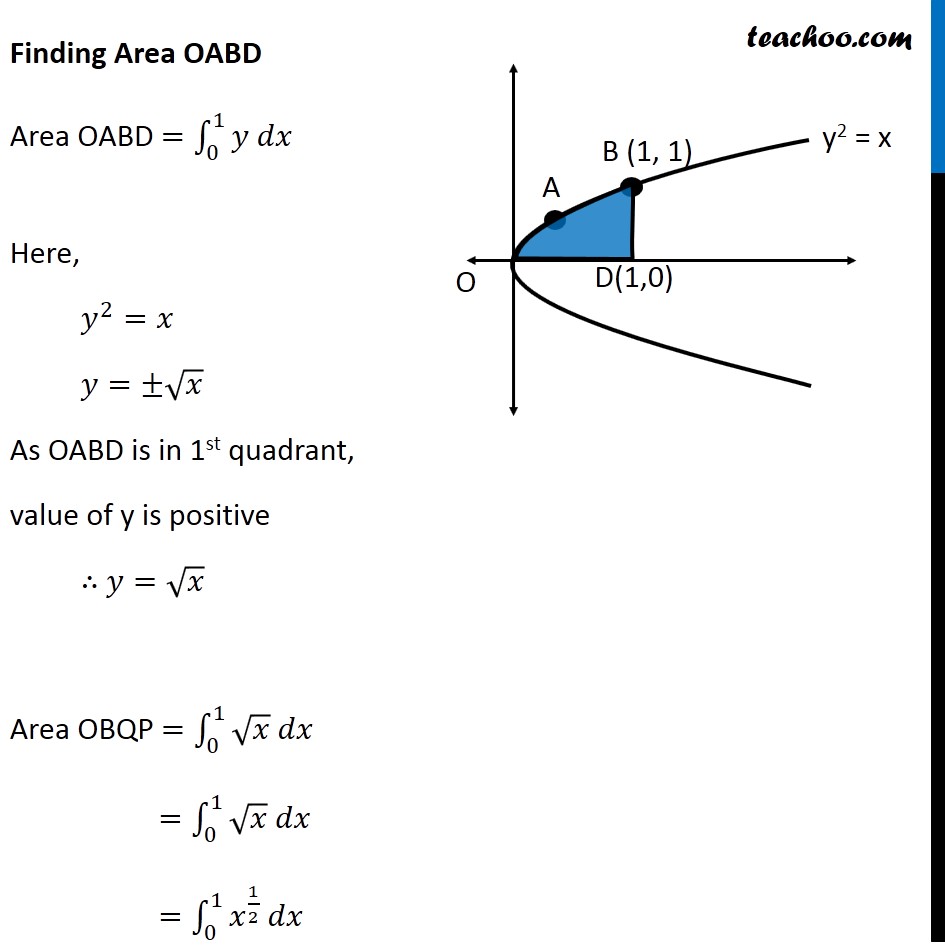
Question 4 Find the area of the region bounded by the two parabolas 𝑦=𝑥2 and 𝑦2 = 𝑥 Drawing figure Here, we have parabolas 𝑦^2=𝑥 𝑥^2=𝑦 Area required = Area OABC Finding Point of intersection B Solving 𝑦2 = 𝑥 𝑥2 =𝑦 Put (2) in (1) 𝑦2 = 𝑥 (𝑥^2 )^2=𝑥 𝑥^4−𝑥=0 𝑥(𝑥^3−1)=0 Finding y – coordinate For 𝒙=𝟎 𝑦=𝑥^2=0^2= 0 So, coordinates are (0 , 0) For 𝒙=𝟏 𝑦=𝑥^2=1^2=1 So, coordinates are (1 , 1) Since point B lies in 1st quadrant So, co-ordinate of B is (1 , 1) Finding Area Area OABC = Area OABD – Area OCBD Finding Area OABD Area OABD =∫_0^1▒〖𝑦 𝑑𝑥〗 Here, 𝑦^2=𝑥 𝑦=±√𝑥 As OABD is in 1st quadrant, value of y is positive ∴ 𝑦=√𝑥 Area OBQP =∫_0^1▒〖√𝑥 𝑑𝑥〗 =∫_0^1▒〖√𝑥 𝑑𝑥〗 =∫_0^1▒〖𝑥^(1/2) 𝑑𝑥〗 = [𝑥^(1/2 + 1)/(1/2 + 1)]_0^1 = [𝑥^(3/2)/(3/2)]_0^1 = 2/3 [𝑥^(3/2) ]_0^1 =2/3 [(1)^(3/2)−(0)^(3/2) ] =2/3 [1−0] =2/3 Area OCBD Area OCBD =∫_0^1▒〖𝑦 𝑑𝑥〗 Here, 𝑥^2=𝑦 𝑦=𝑥^2 Area OAQP =∫_0^1▒〖𝑥^2 𝑑𝑥〗 =[𝑥^(2 + 1)/(2 + 1)]_0^1 =1/3 [𝑥^3 ]_0^1 =1/3 [1^3−0^3 ] =𝟏/𝟑 Therefore, Area OABC = Area OABD – Area OCBD = 2/3−1/3 = 𝟏/𝟑 square units