Example 2 - Chapter 8 Class 10 Introduction to Trignometry

Transcript

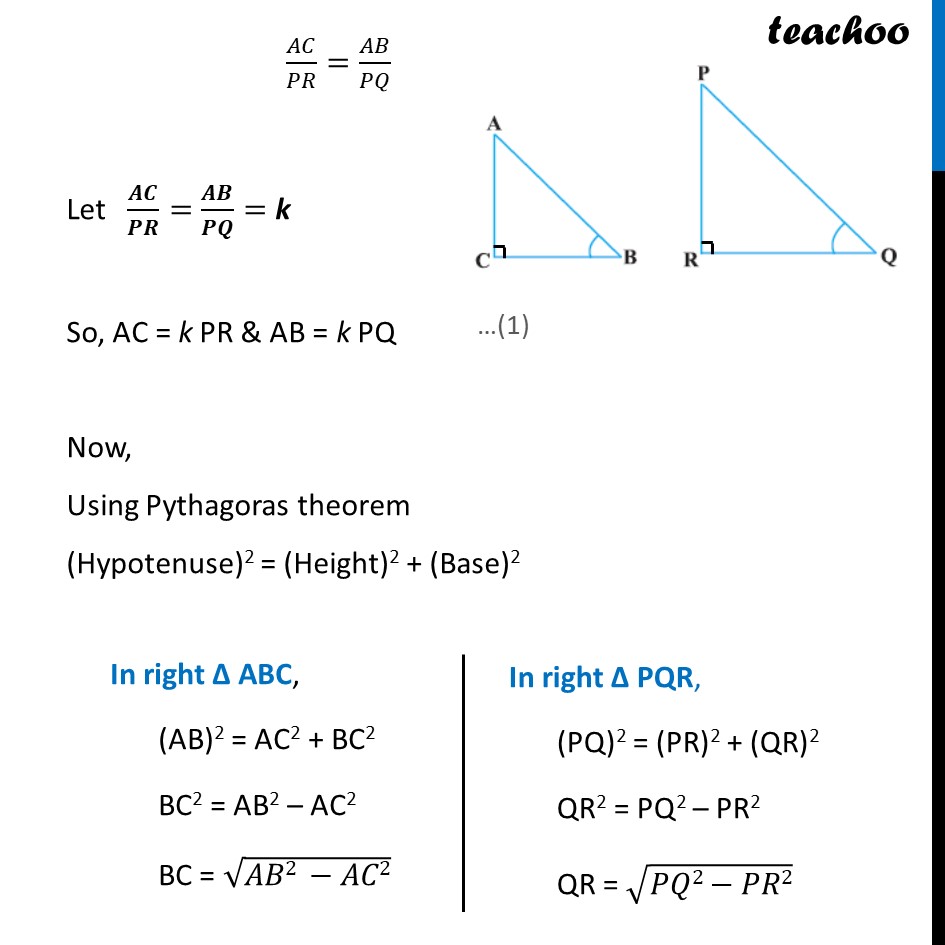
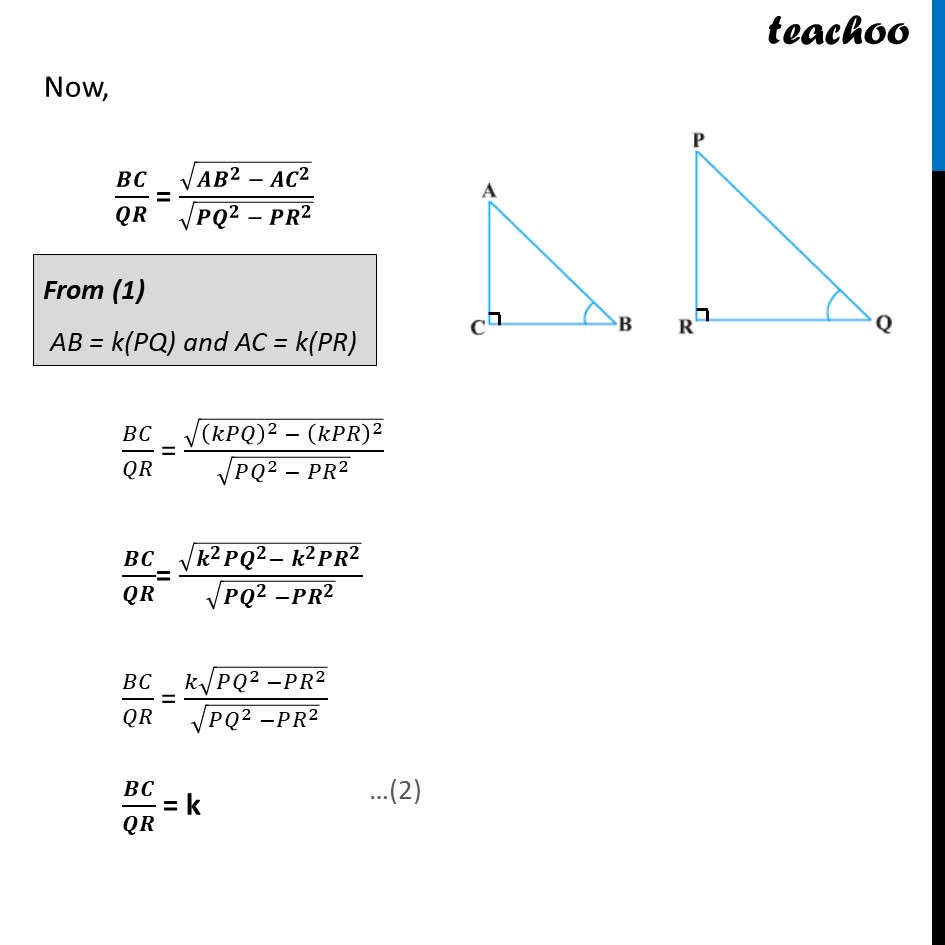
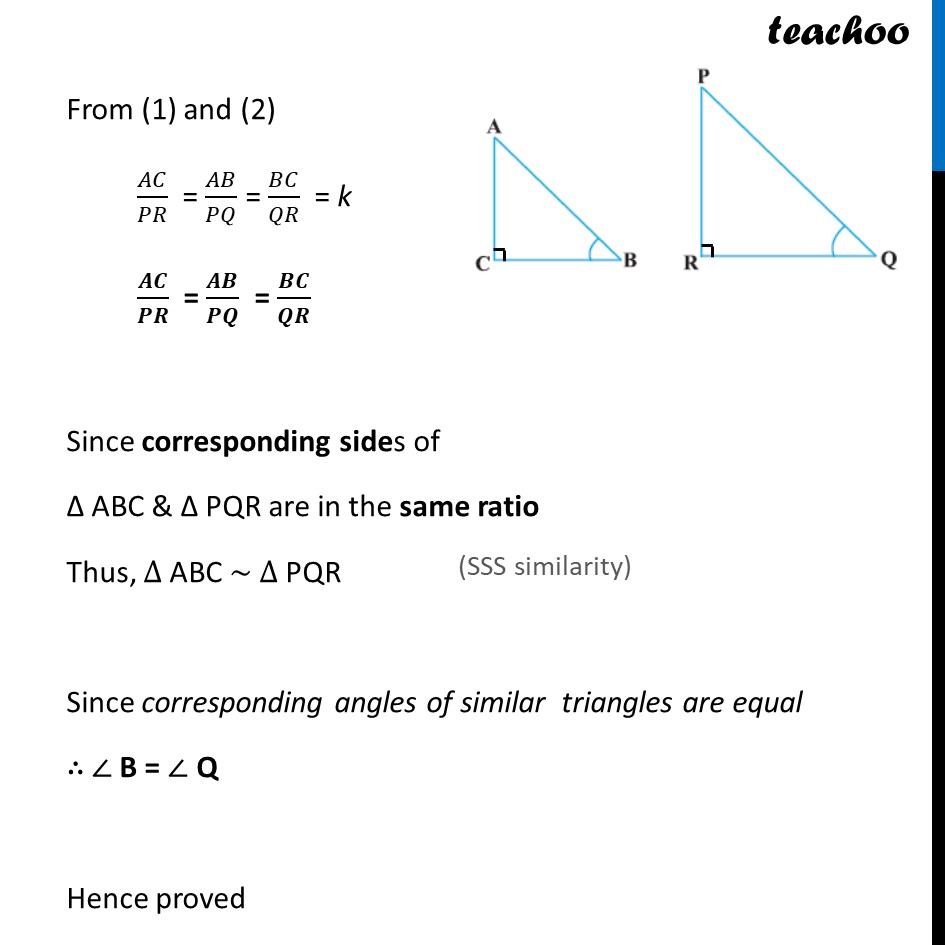
Example 2 If ∠ B and ∠ Q are acute angles such that sin B = sin Q, then prove that ∠ B = ∠ Q. Given: sin B = sin Q To prove: ∠ B = ∠ Q Proof: Let’s take two right angle triangles ABC & PQR Since, sin B = sin Q 𝐴𝐶/𝐴𝐵=𝑃𝑅/𝑃𝑄 𝐴𝐶/𝑃𝑅=𝐴𝐵/𝑃𝑄 Let 𝐴𝐶/𝑃𝑅=𝐴𝐵/𝑃𝑄= k So, AC = k PR & AB = k PQ Now, Using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 Now, 𝐵𝐶/𝑄𝑅 = √(𝐴𝐵2 −𝐴𝐶2)/√(𝑃𝑄2 −𝑃𝑅2) 𝐵𝐶/𝑄𝑅= √((𝑘𝑃𝑄)2−(𝑘𝑃𝑅)2)/√(𝑃𝑄2 −𝑃𝑅2) 𝐵𝐶/𝑄𝑅= √(𝑘2 𝑃𝑄2− 𝑘2𝑃𝑅2)/√(𝑃𝑄2 −𝑃𝑅2) 𝐵𝐶/𝑄𝑅= (𝑘√(𝑃𝑄2−𝑃𝑅2))/√(𝑃𝑄2 −𝑃𝑅2) 𝐵𝐶/𝑄𝑅 = k From (1) and (2) 𝐴𝐶/𝑃𝑅 = 𝐴𝐵/𝑃𝑄 = 𝐵𝐶/𝑄𝑅 = k 𝐴𝐶/𝑃𝑅 = 𝐴𝐵/𝑃𝑄 = 𝐵𝐶/𝑄𝑅 Hence, corresponding sides of Δ ABC & Δ PQR are in the same ratio Thus, ∆ ABC ~ ∆ PQR So, ∠ B = ∠ Q Hence proved