Ex 8.3, 4 (vi) - Chapter 8 Class 10 Introduction to Trignometry

Transcript

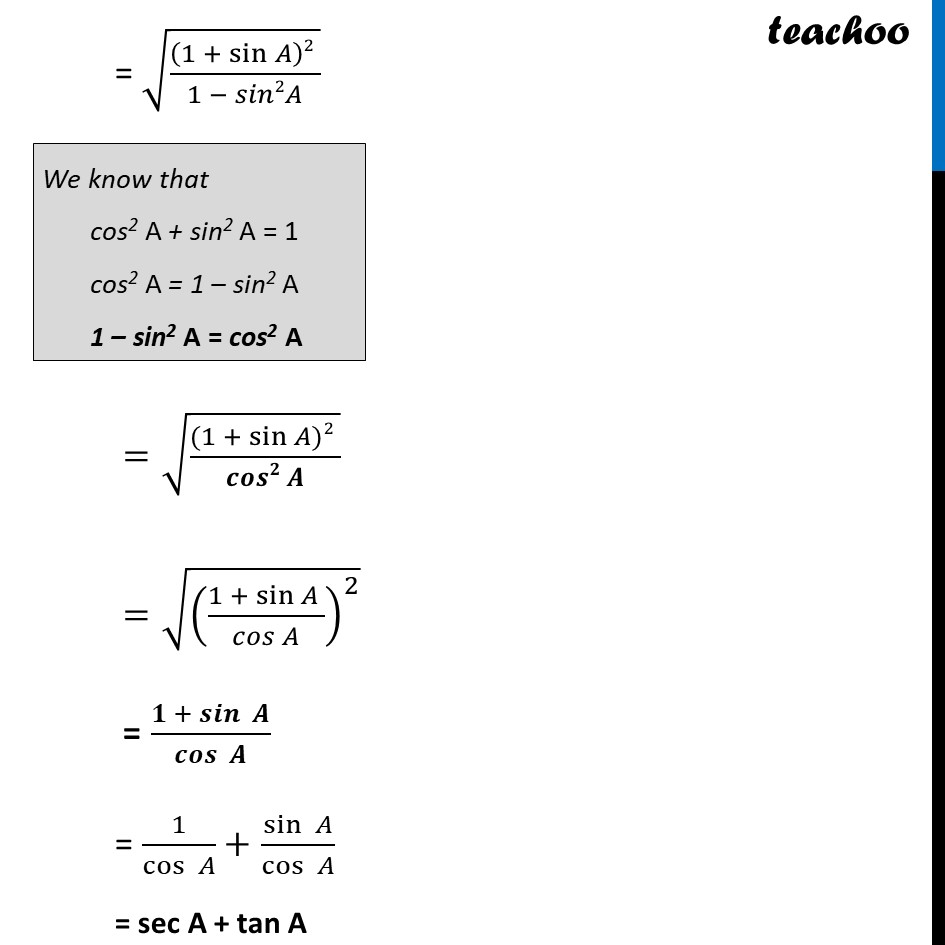
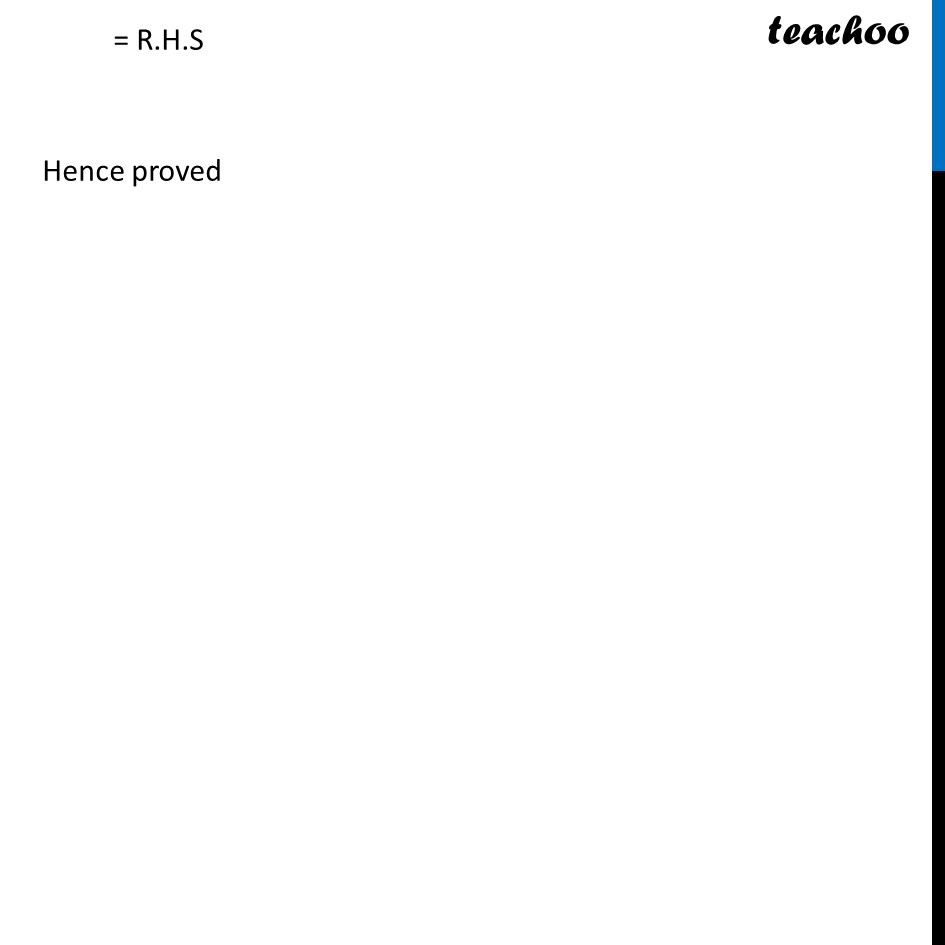
Ex 8.3, 4 Prove the following identities, where the angles involved are acute angles for which the expressions are defined. (vi) √((1 + sin⁡𝐴 )/(1 −〖 sin〗⁡𝐴 )) = sec A + tan A Solving L.H.S √((𝟏 + 𝒔𝒊𝒏⁡𝑨 )/(𝟏 −〖 𝒔𝒊𝒏〗⁡𝑨 )) Rationalizing denominator Multiplying (1 + sin A) in numerator and denominator = √(((𝟏 + 𝐬𝐢𝐧⁡𝑨)(𝟏 + 𝒔𝒊𝒏⁡〖𝑨)〗 )/((𝟏 − 𝐬𝐢𝐧⁡𝑨)(𝟏 + 𝒔𝒊𝒏⁡〖𝑨)〗 )) = √(((1 + sin⁡𝐴 )2 )/(12 − 𝑠𝑖𝑛2𝐴)) = √(((1 + sin⁡𝐴 )2 )/(1 − 𝑠𝑖𝑛2𝐴)) =√(((1 + sin⁡𝐴)2 )/(𝒄𝒐𝒔𝟐 𝑨)) =√(((1 + sin⁡𝐴 )/(𝑐𝑜𝑠 𝐴))^2 ) = (𝟏 + 𝒔𝒊𝒏⁡〖 𝑨〗)/𝒄𝒐𝒔⁡〖 𝑨〗 = 1/cos⁡〖 𝐴〗 + sin⁡〖 𝐴〗/cos⁡〖 𝐴〗 = sec A + tan A = R.H.S Hence proved