CBSE Class 10 Sample Paper for 2019 Boards
You are here
CBSE Class 10 Sample Paper for 2019 Boards
Last updated at Dec. 16, 2024 by Teachoo
Question 19 (OR 2 nd Question)
In ∆ABC, if AD is the median, then show that AB 2 + AC 2 = 2(AD 2 + BD 2 )
Transcript
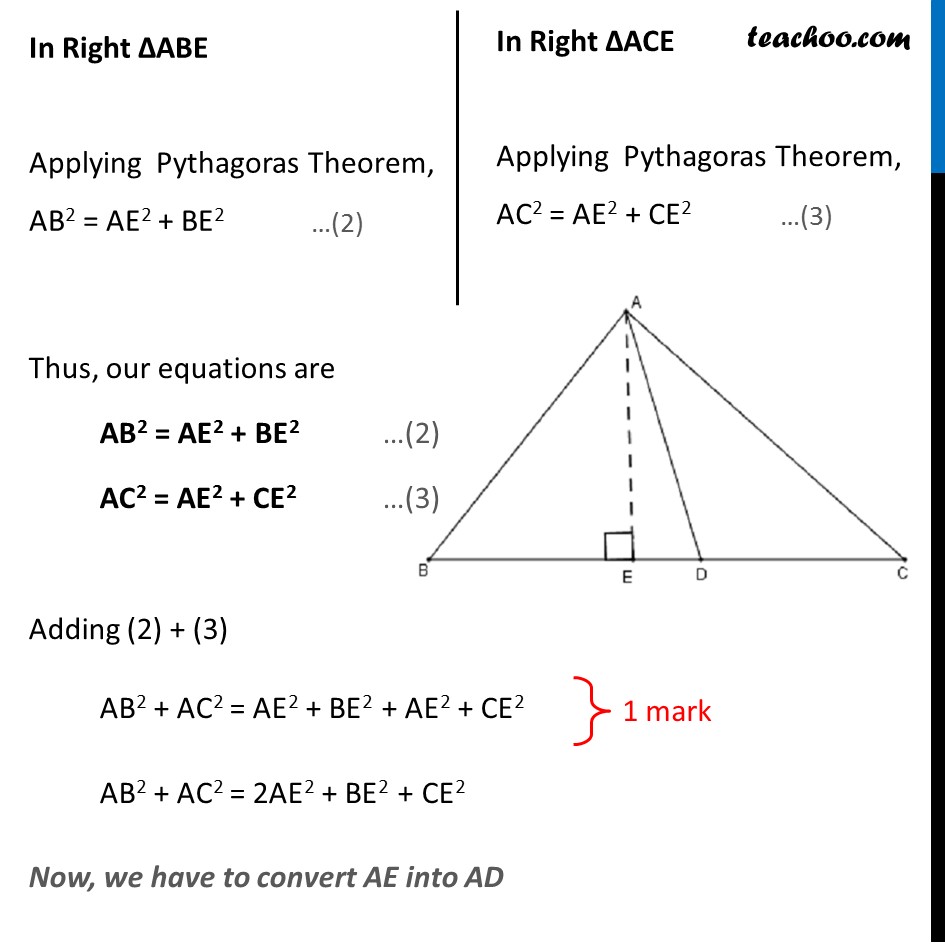
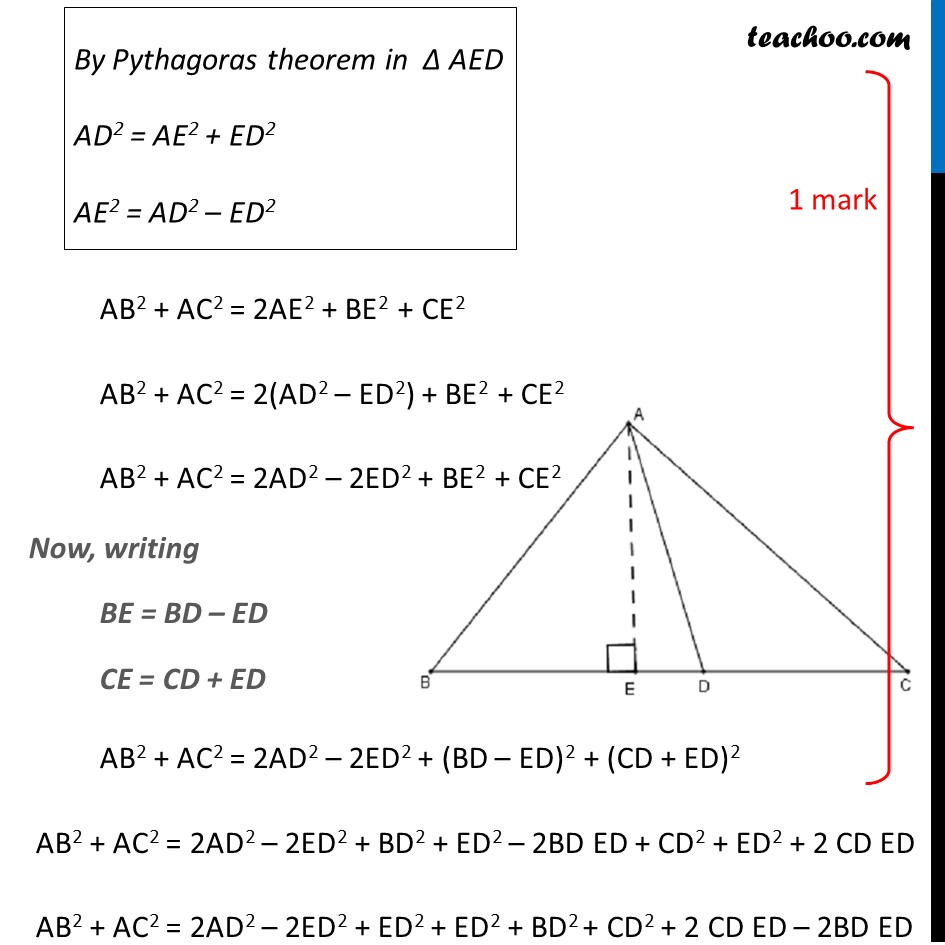
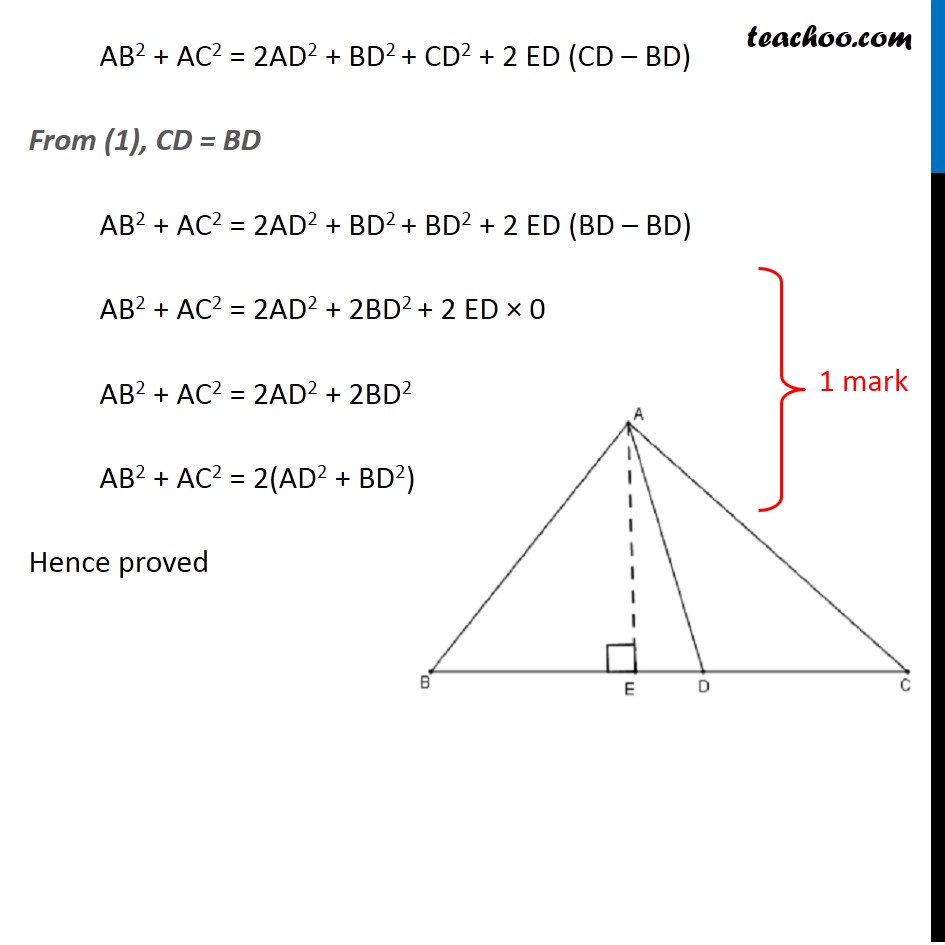
Question 19 (OR 2nd Question) In ∆ABC, if AD is the median, then show that AB2 + AC2 = 2(AD2 + BD2) Given: AD is a Median of ∆ABC ∴ BD = CD Also, AE ⊥ BC To Prove: AB2 + AC2 = 2(AD2 + BD2) Proof : In Right ∆ABE Applying Pythagoras Theorem, AB2 = AE2 + BE2 In Right ∆ACE …(2) Applying Pythagoras Theorem, AC2 = AE2 + CE2 …(3) …(3) By Pythagoras theorem in Δ AED AD2 = AE2 + ED2 AE2 = AD2 – ED2 By Pythagoras theorem in Δ AED AD2 = AE2 + ED2 AE2 = AD2 – ED2 AB2 + AC2 = 2AE2 + BE2 + CE2 AB2 + AC2 = 2(AD2 – ED2) + BE2 + CE2 AB2 + AC2 = 2AD2 – 2ED2 + BE2 + CE2 Now, writing BE = BD – ED CE = CD + ED AB2 + AC2 = 2AD2 – 2ED2 + (BD – ED)2 + (CD + ED)2 AB2 + AC2 = 2AD2 – 2ED2 + BD2 + ED2 – 2BD ED + CD2 + ED2 + 2 CD ED AB2 + AC2 = 2AD2 – 2ED2 + ED2 + ED2 + BD2 + CD2 + 2 CD ED – 2BD ED AB2 + AC2 = 2AD2 + BD2 + CD2 + 2 ED (CD – BD) From (1), CD = BD AB2 + AC2 = 2AD2 + BD2 + BD2 + 2 ED (BD – BD) AB2 + AC2 = 2AD2 + 2BD2 + 2 ED × 0 AB2 + AC2 = 2AD2 + 2BD2 AB2 + AC2 = 2(AD2 + 2BD2) Hence proved
