Question 14 - CBSE Class 10 Sample Paper for 2019 Boards

Transcript

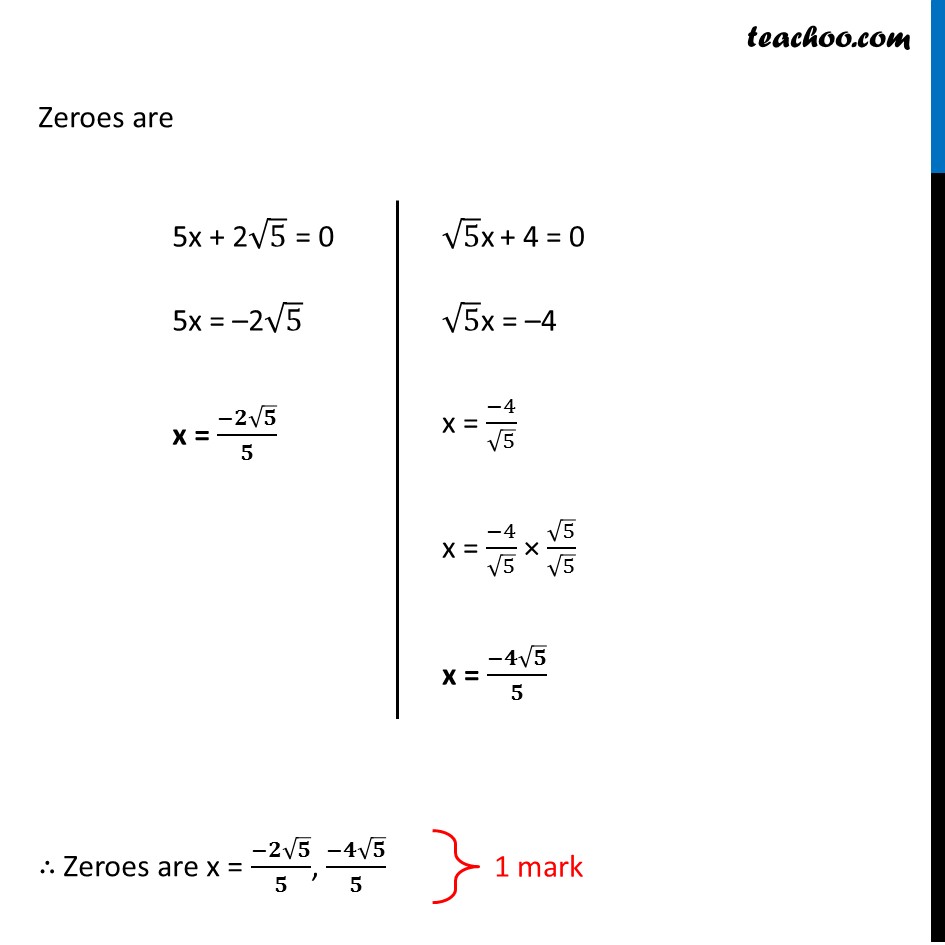
Question 14 (Method 1 – Using Splitting the middle term) Find the zeroes of the following polynomial: 5√5 x2 + 30x + 8√5 5√5 x2 + 30x + 8√5 Factorising by splitting the middle term = 5√5 x2 + 20x + 10x + 8√5 = 5√5 x2 + 20x + (5 × 2)x + 8√5 = 5√5 x2 + 20x + (√5 × √5 × 2)x + 8√5 = 5x(√5 x + 4) + √5 × 2(√5 x + 4) = 5x(√5 x + 4) + 2√5 (√5 x + 4) = (5x + 2√5) (√5x + 4) Splitting the middle term method We need to find two numbers whose Sum = 30 Product = 5√5 × 8 √5 = 5 × 8 × √5 × √5 = 40 × 5 = 200 Zeroes are 5x + 2√5 = 0 5x = –2√5 x = (−𝟐√𝟓)/𝟓 √5x + 4 = 0 √5x = –4 x = (−4)/√5 x = (−4)/√5 × √5/√5 x = (−𝟒√𝟓)/𝟓 √5x + 4 = 0 √5x = –4 x = (−4)/√5 x = (−4)/√5 × √5/√5 x = (−𝟒√𝟓)/𝟓 1 mark Question 14 (Method 2 – Using D formula) Find the zeroes of the following polynomial: 5√5 x2 + 30x + 8√5 5√5 x2 + 30x + 8√5 Comparing with ax2 + bx + c a = 5√5, b = 30, c = 8√5 Now, x = (−𝑏 ± √(𝑏^2 − 4𝑎𝑐))/2𝑎 = (−30 ± √(〖(30)〗^2 − 4 × 5√5 × 8√5) )/(2 × 5√5) = (−30 ± √(900 − 4 × 5 × 8 × √5 × √5) )/(10√5) = (−30 ± √(900 − 4 × 5 × 8 × 5))/(10√5) = (−30 ± √(900 −20 × 40))/(10√5) = (−30 ± √(900 − 800))/(10√5) = (−30 ± √100)/(10√5) = (−30 ± 10)/(10√5) 1.5 marks Therefore, x = (−30 + 10)/(10√5) x = (−20)/(10√5) x = (−2)/√5 x = (−2)/√5 × √5/√5 x = (−𝟐√𝟓)/𝟓 x = (−30 − 10)/(10√5) x = (−40)/(10√5) x = (−4)/√5 x = (−4)/√5 × √5/√5 x = (−𝟒√𝟓)/𝟓 . ∴ Zeroes are x = (−𝟐√𝟓)/𝟓, (−𝟒√𝟓)/𝟓 1.5 marks